
Concept explainers
(a)
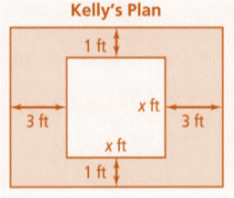
To find: The polynomial that represents the area of Kelly’s plot.
(a)
Answer to Problem 1MP
Explanation of Solution
Given Information:
Formula Used:
Area of a rectangle of length l and width b is lb
Calculation:
Length of Kelly’s plot, l =
Width of Kelly’s plot, b =
Length and width of Kelly’s plot are binomials (since it contains two terms)
Therefore the area is the product of two binomials.
Area of Kelly’s plot,
(b)
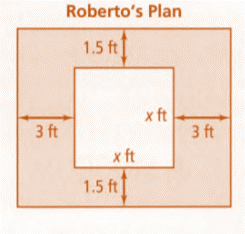
To find: The polynomial that represents the area of Roberto’s plot.
(b)
Answer to Problem 1MP
Explanation of Solution
Given Information:
Formula Used:
Area of a rectangle of length l and width b is lb
Calculation:
Length of Roberto’s plot, l =
Width of Roberto’s plot, b =
Length and width of Roberto’s plot are binomials (since it contains two terms)
Therefore the area is the product of two binomials.
Area of Roberto’s plot,
(c)
To check: the products found in (a) and (b) are correct by applying a value for x.
(c)
Explanation of Solution
Given Information:
Kelly’s plot Length =
Breadth=
Roberto’s plot Length =
Breadth =
Proof:
Let’s assume that
For Kelly’s plot Length = 7
Breadth= 3
Area =
Now let’s compute the area using
Which is same as
Roberto’s plot Length = 7
Breadth= 4
Area =
Now let’s compute the area using
Which is same as
∴The polynomials found in (a) and (b) are correct.
(d)
To check: whether the area of Roberto’s plot is greater than Kelly’s plot.
(d)
Answer to Problem 1MP
Area of Roberto’s plot is greater than that of Kelly’s plot.
Explanation of Solution
Given Information:
The area of Roberto’s plot is
The area of Kelly’s plot is
Proof:
From part (c)
For
The area of Roberto’s plot = 28 sq.ft
The area of Kelly’s plot = 21 sq.ft
That is, for
Area of Roberto’s plot is greater than that of Kelly’s plot……. (1)
Since the area is true for all values of x, (1) is true for all values of x
Chapter 8 Solutions
High School Math 2015 Common Core Algebra 1 Student Edition Grade 8/9
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
Elementary Statistics: Picturing the World (7th Edition)
Elementary Statistics (13th Edition)
Precalculus
Elementary Statistics
Calculus: Early Transcendentals (2nd Edition)
- In simplest terms, Sketch the graph of the parabola. Then, determine its equation. opens downward, vertex is (- 4, 7), passes through point (0, - 39)arrow_forwardIn simplest way, For each quadratic relation, find the zeros and the maximum or minimum. a) y = x 2 + 16 x + 39 b) y = 5 x2 - 50 x - 120arrow_forwardIn simplest terms and step by step Write each quadratic relation in standard form, then fi nd the zeros. y = - 4( x + 6)2 + 36arrow_forward
- In simplest terms and step by step For each quadratic relation, find the zeros and the maximum or minimum. 1) y = - 2 x2 - 28 x + 64 2) y = 6 x2 + 36 x - 42arrow_forwardWrite each relation in standard form a)y = 5(x + 10)2 + 7 b)y = 9(x - 8)2 - 4arrow_forwardIn simplest form and step by step Write the quadratic relation in standard form, then fi nd the zeros. y = 3(x - 1)2 - 147arrow_forward
- Step by step instructions The path of a soccer ball can be modelled by the relation h = - 0.1 d 2 + 0.5 d + 0.6, where h is the ball’s height and d is the horizontal distance from the kicker. a) Find the zeros of the relation.arrow_forwardIn simplest terms and step by step how do you find the zeros of y = 6x2 + 24x - 192arrow_forwardStep by step Find the zeros of each quadratic relation. a) y = x2 - 16xarrow_forward
- In simplest step by step terms, how do you find the zeros of y = x2 - 16arrow_forwardIn simplest terms, Describe the shape and position of the parabola relative to the graph of y = x 2 y = - 80( x + 9) 2 + 10.8arrow_forwardas a Identify each equation Parabola, circle, ellipse perbola without completio the square. x²-6x-14 y = 33-y² 14y ofarrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





