
Concept explainers
a.
To complete:
The given table using given equation.
a.
Answer to Problem 11E
The complete table would be:
| t | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| d | 0 | 120 | 240 | 360 | 480 | 600 | 720 |
Explanation of Solution
Given:
In 1997, the pathfinder spacecraft landed on Mars.It contained a robotic vehicle named Sojourner that could roam up to 500 meters from the lander. The distance d (in meters) that Sojourner could travel in t hours in given by
| t | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| d |
Calculation:
To complete our given table, we will substitute the given values of t in our given equation as:
Therefore, the complete table would be:
| t | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| d | 0 | 120 | 240 | 360 | 480 | 600 | 720 |
b.
To graph:
The equation
b.
Answer to Problem 11E
The graph of the equation would look like:
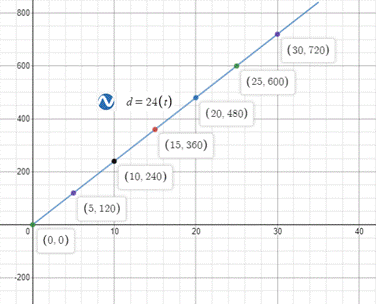
Explanation of Solution
Given:
In 1997, the pathfinder spacecraft landed on Mars. It contained a robotic vehicle named Sojourner that could roam up to 500 meters from the lander. The distance d (in meters) that Sojourner could travel in t hours in given by
Calculation:
Upon graphing our given equation, we will get our required graph as shown below:
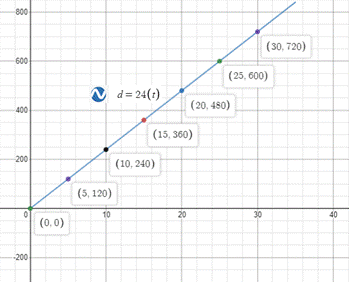
c.
To find:
The point on the graph whose d-coordinate is 500, and estimate the t -coordinate of this point. How much time would it take Sojourner to reach its maximum distance from the lander?
c.
Answer to Problem 11E
It will take approximately 20.83 hours for Sojourner to reach its maximum height.
Explanation of Solution
Given:
In 1997, the pathfinder spacecraft landed on Mars. It contained a robotic vehicle named Sojourner that could roam up to 500 meters from the lander. The distance d (in meters) that Sojourner could travel in t hours in given by
Calculation:
To find the t -coordinate of the point whose d -coordinate is 500, we will substitute
Therefore, the t -coordinate of the point would be approximately 20.83.
Since Sojourner can roam up to 500 meters from the lander, therefore, it will take approximately 20.83 hours for Sojourner to reach its maximum height.
Chapter 8 Solutions
EBK PRE-ALGEBRA
Additional Math Textbook Solutions
A First Course in Probability (10th Edition)
Algebra and Trigonometry (6th Edition)
Elementary Statistics
University Calculus: Early Transcendentals (4th Edition)
Pre-Algebra Student Edition
College Algebra with Modeling & Visualization (5th Edition)
- Solve the following systems of equations and show all work.y = x2 + 3y = x + 5 Please type out answerarrow_forwardSolve the following system of equations. Show all work and solutions.y = 2x2 + 6x + 1y = −4x2 + 1 Please type out answerarrow_forwardDalia buys 20 collectible gems per month. Grace sells 10 gems from her collection of 120 each month. When will Dalia have more gems than Grace? Show your work. Dear Student If You Face any issue let me know i will solve your all doubt. I will provide solution again in more detail systematic and organized way. I would also like my last 3 questions credited to mearrow_forward
- Dalia buys 20 collectible gems per month. Grace sells 10 gems from her collection of 120 each month. When will Dalia have more gems than Grace? Show your work.arrow_forwardSolve the following system of equations. Show all work and solutions.y = 2x2 + 6x + 1y = −4x2 + 1arrow_forwardSolve the following systems of equations and show all work.y = x2 + 3y = x + 5arrow_forward
- Write an equation for the function shown. You may assume all intercepts and asymptotes are on integers. The blue dashed lines are the asymptotes. 10 9- 8- 7 6 5 4- 3- 2 4 5 15-14-13-12-11-10 -9 -8 -7 -6 -5 -4 -3 -2 1 1 2 3 -1 -2 -3 -4 1 -5 -6- -7 -8- -9 -10+ 60 7 8 9 10 11 12 13 14 15arrow_forwardUse the graph of the polynomial function of degree 5 to identify zeros and multiplicity. Order your zeros from least to greatest. -6 3 6+ 5 4 3 2 1 2 -1 -2 -3 -4 -5 3 4 6 Zero at with multiplicity Zero at with multiplicity Zero at with multiplicityarrow_forwardUse the graph to identify zeros and multiplicity. Order your zeros from least to greatest. 6 5 4 -6-5-4-3-2 3 21 2 1 2 4 5 ૪ 345 Zero at with multiplicity Zero at with multiplicity Zero at with multiplicity Zero at with multiplicity པ་arrow_forward
- Use the graph to write the formula for a polynomial function of least degree. -5 + 4 3 ♡ 2 12 1 f(x) -1 -1 f(x) 2 3. + -3 12 -5+ + xarrow_forwardUse the graph to identify zeros and multiplicity. Order your zeros from least to greatest. 6 -6-5-4-3-2-1 -1 -2 3 -4 4 5 6 a Zero at with multiplicity Zero at with multiplicity Zero at with multiplicity Zero at with multiplicityarrow_forwardUse the graph to write the formula for a polynomial function of least degree. 5 4 3 -5 -x 1 f(x) -5 -4 -1 1 2 3 4 -1 -2 -3 -4 -5 f(x) =arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





