
Interpretation:
For a bar magnet system
Concept Introduction:
Determine the fixed point for the given system.
Determine the bifurcation using the Jacobian matrix and fixed point.
Sketch phase portrait using system equation.
Answer to Problem 12E
Solution:
The fixed point of the system is
It is shown that a bifurcation occurs at
It is shown that the system is a “gradient” system,
It is proved that the system has no periodic orbits.
The phase portrait for
Explanation of Solution
Consider the Interacting bar magnets system with system equation
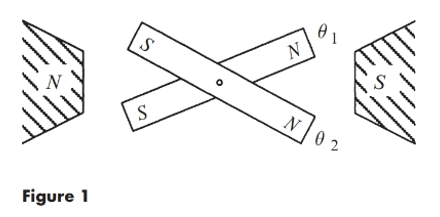
To calculate the fixed point of the system, equationsare as:
For the calculation of the fixed point of the above system equation, first equating the first derivative of the above system equation to zero.
Substitute
From the trigonometric identity,
Hence,
Substitute
From the trigonometric identity,
To obtain
Using trigonometric identity,
Apply trigonometric expression in the above expression of the fixed point,
From the above,
By solving,
Similarly,
Compare the above expression of
Substitute
Therefore, the fixed point of the above system equation is
Bifurcation is defined as the point or area at which something is divided into two parts and branches. The point in the system equation at which bifurcating occur.
For the calculation of the type of bifurcation, the Jacobian matrix is:
By substituting
The Jacobian matrix at the fixed point
The trace of the above Jacobian matrix is calculated as:
The determinant of the above Jacobian matrix is calculated as:
Therefore, from the above calculation of the system equation, the determinant of the above system equation at the fixed point is zero, so the bifurcation is saddle node bifurcation.
The calculation of the potential gradient of the given systemis shown below.
The expression of the potential function is:
Substitute
Therefore, the potential function for the value of
Similarly, for
Substitute
Therefore, the potential function for the value of
For the calculation of the periodic orbit,
Add the potential function.
From the trigonometric identity,
Hence,
For the periodicity of the above system equation, calculate the closed orbit of the above system equation with the help of the Greens theorem,
Therefore, from above calculation of the potential function, it is clear that the system has no periodic orbit.
A phase portrait is defined as the geometrical representation of the trajectories of the dynamical system in the phase plane of the system equation. Every set of the initial condition is represented by a different curve or point in the phase plane.
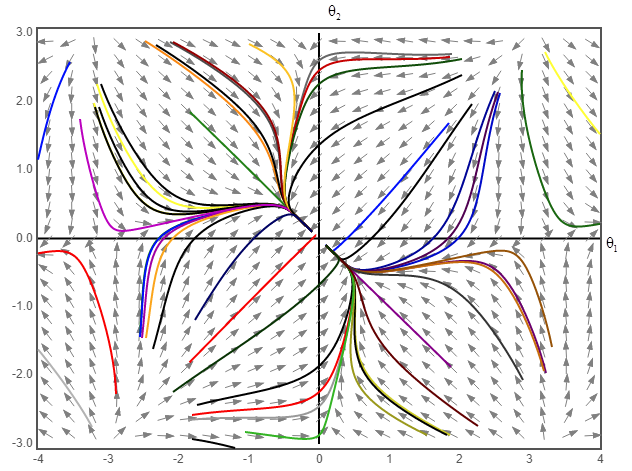
The phase portrait for the given system equation is shown. The system equations are given as:
The phase portrait plot for the above system equation for the value of K lying in the range of
The phase portrait of the above system equation at
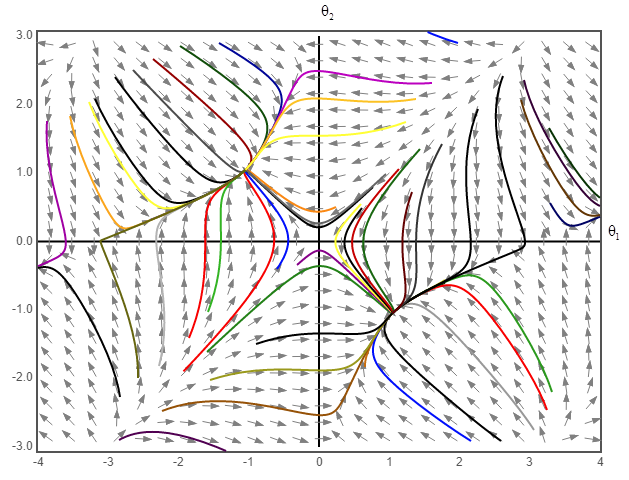
The phase portrait plot for the above system equation for the value of K lying in the range of
The phase portrait of the above system equation at
Want to see more full solutions like this?
Chapter 8 Solutions
EBK NONLINEAR DYNAMICS AND CHAOS WITH S
- 5.8 A reinforced concrete column is 12 feet long, and un- der load, it shortens 3 inches". Determine its average unit strain. Average Unit Strainarrow_forward5.10 A 500-foot-long steel cable is loaded in tension and registers an average unit strain of 0.005. Determine the total elongation due to this load. Total Elongationarrow_forward5.14 A 100-foot-long surveyor's steel tape with a cross- sectional area of 0.006 square inch must be stretched with a pull of 16# when in use. If the modulus of elasticity of this steel is E = 30,000 ksi, (a) what is the total elongation 8 in the 100 foot tape and (b) what unit tensile stress is pro- duced by the pull? a. Elongation b. Tensile Stressarrow_forward
- Obtain the voltage across the capacitor for the following input: (a) 5Volts; (b) 3sin(t); (c) 2 cos(t). Use Laplace transform and Cramer's rule.arrow_forwardObtain the voltage across the capacitor for the following input: (a) 5Volts; (b) 3sin(t); (c) 2 cos(t). Use Laplace transform and Cramer's rule.arrow_forwardObtain the voltage across the capacitor for the following input: (a) 5Volts; (b) 3sin(t); (c) 2 cos(t). Use Laplace transform and Cramer's rule.arrow_forward
- v(t) + R₁ = 1 ohm W R2 = 1 ohm www i1(t) 0000 L = 2H i2(t) C 1F + vc(t)arrow_forwardObtain the voltage across the capacitor for the following input: (a) 5Volts; (b) 3sin(t); (c) 2 cos(t). Use Laplace transform and Cramer's rule.arrow_forwardFor communcation marks. In the questions answered above should have the criteria show proper mathematical form use proper symbols, notations, conventions, graph(s) where applicable solution is neat, clear and easy to follow If you write on the paper in online version you will be assigned 0 marks except graph.arrow_forward
- a) If is a polynomial function, does always have to have a horizontal asymptote? If no, provide a counterexample. ax+b b) Write an equation for a rational function whose graph of the formex+d where f(x) has all the indicated features. X-intercept of 14 Y-intercept of -1/2 VA with equation -2/3 HA with equation 4/3arrow_forwardAn airplane has a speed of 400 km/h with no wind. The airplane flies 2140 km with the wind. The airplane can only fly 1860 km against the wind in the same time. If w represents the speed of the wind, create an equation could be used to solve for w? Find the speed f the wind. hint; Use Time = Distance / speedarrow_forwardx²+8x+15 f(x) = Consider the function. x²-x-12 a) Determine the following key features of the function: i) domain and range ii) intercepts iii) equations of any asymptotes and holes iv) intervals where the function is increasing and intervals where the function is decreasing v) Sketch the graph.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning

