Chapter 8, Problem 23P

Many fields of engineering require accurate population estimates. For example, transportation engineers might find it necessary to determine separately the population growth trends of a city and adjacent suburb. The population of the urban area is declining with time according to

$P_u\left(t\right)=P_{u,\text{max}}{e}^{-k_{n}t}+P_{u,\text{min}}$

while the suburban population is growing, as in

$P_s\left(t\right)=\frac{P_{s,\text{max}}}{1+\left[P_{s,max}\text{/}{P}_0-1\right]e^{-k_{s}t}}$

where $P_{s,\text{ max}},k_{u,}{P}_{s,\text{ max}},P_0,\text{ and }{k}_s=$ empirically derived parameters. Determine the time and corresponding values of $p_u\left(t\right)\text{ and }{p}_s\left(t\right)$ when the suburbs are 20% larger than the city. The parameter values are $P_{u,\text{ max}}=75,000,k_u=0.045\text{/yr,}{P}_{u,\text{min}}=100,000\text{ people,}$ $P_{s,max}=300,000\text{ people, }{P}_0=10,000\text{ people, }{k}_s=0.8\text{/yr}$. To obtain your solutions. Use (a) graphical, (b) false-position, and (c) modified secant methods.

To determine

To calculate: The values of the urban and sub-urban population and the corresponding time where the urban population is given by the formula $P_u\left(t\right)=P_{u,\max }{e}^{-k_{u}t}+P_{u,\min }$ and the sub-urban population is given by the formula $P_s\left(t\right)=\frac{P_{s,\max }}{1+\left[\frac{P_{s,\max }}{P_0}-1\right]e^{-k_{s}t}}$ for the parameters $P_{u,\max }=75000$, $P_{u,\min }=100000,k_u=0.045,k_s=0.08,P_{S,\max }=300000$, and $P_0=10000$ using the graphical method and with the additional information that at time t, the suburbs are 20% larger than the city.

Answer to Problem 23P

Solution: After 40 years, the suburban population would be 1.2 times the urban population with the populations of the suburban and urban areas being 137482 and 112487, respectively.

Explanation of Solution

Given Information:

The expression, $P_u\left(t\right)=P_{u,\max }{e}^{-k_{u}t}+P_{u,\min }$ and $P_s\left(t\right)=\frac{P_{s,\max }}{1+\left[\frac{P_{s,\max }}{P_0}-1\right]e^{-k_{s}t}}$

for the parameters $P_{u,\max }=75000,P_{u,\min }=100000,k_u=0.045,k_s=0.08,P_{S,\max }=300000$, and $P_0=10000$ where the suburbs are 20% larger than the city at time t.

Calculation:

Substitute 75000 for $P_{u,\max }$, 100000 for $P_{u,\min }$, and $0.045$ for $k_u$ in the formula for the urban population to obtain,

$P_u\left(t\right)=75000e^{-0.045t}+100000$ …… (1)

Substitute 300000 for $P_{s,\max }$, 10000 for $P_0$ and 0.08 for $k_s$ in the formula for the suburban population to obtain,

$P_s\left(t\right)=\frac{300000}{1+\left[\frac{300000}{10000}-1\right]e^{-0.08t}}$

$P_s\left(t\right)=\frac{300000}{1+29e^{-0.08t}}$ …… (2)

It has been provided that at time t, the suburban population is 20% larger than the urban population, that is, 1.2 times the urban population. Thus, from equation (1) and equation (2),

$1.2\left(75000e^{-0.045t}+100000\right)=\frac{300000}{1+29e^{-0.08t}}$

This equation can be rewritten in the form of a following function whose zero corresponds with the root of the equation,

$f\left(t\right)=1.2\left(75000e^{-0.045t}+100000\right)-\frac{300000}{1+29e^{-0.08t}}$

The desired value of t can be found by plotting the function f with respect to t and then computing the value at which the function crosses the x-axis.

Use the following MATLAB code to plot the function $f\left(t\right)$ with respect to t.

clear;clc;

% Create a discrete space for t

t=linspace(0, 100);

% Enter the function

f=1.2*(75000*exp(-0.045*t)+100000)-(300000./(1+29*exp(-0.08*t)));

% Plot the function w.r.t t and locate the value of y where t=0.

plot(t, f);

xlabel('t');ylabel('f(t)');grid;

Execute the above code to obtain the plot as,

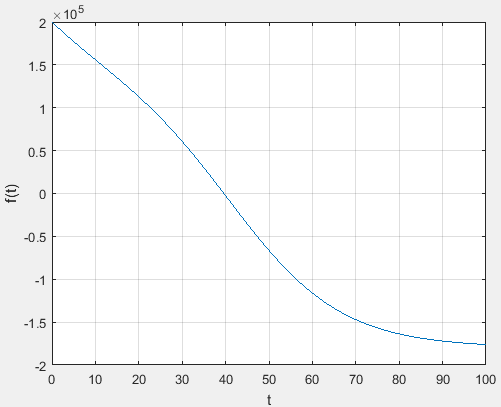
From the graph, the curve crosses horizontal axis through the origin at approximately $40$; thus, it can be concluded that after 40 years, the suburban population is 1.2 times the urban population.

Substitute 40 for t in the formula for the urban population to get,

$\begin{array}{c}{P}_u\left(t\right)=75000e^{-0.045\left(40\right)}+100000\\ \approx 112397\end{array}$

Hence, the urban population after 40 years is 112397.

Substitute 40 for t in the formula for the suburban population to get,

$\begin{array}{c}{P}_s\left(t\right)=\frac{300000}{1+29e^{-0.08\left(40\right)}}\\ \approx 137482\end{array}$

Hence, the suburban population after 40 years is 137482.

To determine

To calculate: The values of the urban and sub-urban population and the time where the urban population is given by the formula $P_u\left(t\right)=P_{u,\max }{e}^{-k_{u}t}+P_{u,\min }$ and the sub-urban population is given by the formula $P_s\left(t\right)=\frac{P_{s,\max }}{1+\left[\frac{P_{s,\max }}{P_0}-1\right]e^{-k_{s}t}}$ for the parameters, $P_{u,\max }=75000$, $P_{u,\min }=100000,k_u=0.045,k_s=0.08,P_{S,\max }=300000$, and $P_0=10000$ using the false-position method with the additional information that at time t, the suburbs are 20% larger than the city.

Answer to Problem 23P

Solution: After 39.6068 years, the suburban population would be 1.2 times the urban population with the populations of the suburban and urban areas being 13 5142.5 and 112 618.7, respectively.

Explanation of Solution

Given Information:

The expressions, $P_u\left(t\right)=P_{u,\max }{e}^{-k_{u}t}+P_{u,\min }$ and $P_s\left(t\right)=\frac{P_{s,\max }}{1+\left[\frac{P_{s,\max }}{P_0}-1\right]e^{-k_{s}t}}$ for the parameters $P_{u,\max }=75000$, $P_{u,\min }=100000$, $k_u=0.045,k_s=0.08,P_{S,\max }=300000$, and $P_0=10000$ where the suburbs are 20% larger than the city at time t.

Formula used:

An equation $f\left(x\right)=0$ can be solved by the false position method over the interval $\left[a,b\right]$ as follows,

Step 1- Compute $x_1$ from the formula $x_1=f\left(a\right)-\frac{\left(b-a\right)f\left(a\right)}{f\left(b\right)-f\left(a\right)}$.

Step 2- If $f\left(a\right)f\left(x_1\right)<0$, replace b by $x_1$ or else, replace a by $x_1$.

Step 3- Proceed with the same procedure till ${\epsilon }_a<{\epsilon }_s$.

Calculation:

Substitute 75000 for $P_{u,\max }$, 100000 for $P_{u,\min }$, and $0.045$ for $k_u$ in the formula for the urban population to obtain,

$P_u\left(t\right)=75000e^{-0.045t}+100000$

Substitute 300000 for $P_{s,\max }$, 10000 for $P_0$, and 0.08 for $k_s$ in the formula for the suburban population to obtain,

$\begin{array}{c}{P}_s\left(t\right)=\frac{300000}{1+\left[\frac{300000}{10000}-1\right]e^{-0.08t}}\\ P_s\left(t\right)=\frac{300000}{1+29e^{-0.08t}}\end{array}$

It has been provided that at time t, the suburban population is 20% larger than the urban population or 1.2 times the urban population. Thus,

$1.2\left(75000e^{-0.045t}+100000\right)=\frac{300000}{1+29e^{-0.08t}}$

The above equation can be rewritten in the form of a following function whose zero corresponds with the root of the equation,

$f\left(t\right)=1.2\left(75000e^{-0.045t}+100000\right)-\frac{300000}{1+29e^{-0.08t}}$

The desired value of t can be found using the false position method.

Let the initial interval be $\left[0,100\right]$.

Then,

$\begin{array}{c}f\left(0\right)=1.2\left(75000e^{-0.045\left(0\right)}+100000\right)-\frac{300000}{1+29e^{-0.08\left(0\right)}}\\ =200000\\ f\left(100\right)=1.2\left(75000e^{-0.045\left(100\right)}+100000\right)-\frac{300000}{1+29e^{-0.08\left(100\right)}}\\ =-176110\end{array}$

As $f\left(0\right)f\left(100\right)<0$, the root lies in the interval.

Now proceed with the first iteration as follows,

$\begin{array}{c}{x}_1=f\left(0\right)-\frac{\left(100-0\right)f\left(100\right)}{f\left(100\right)-f\left(0\right)}\\ =53.1760\end{array}$

Further,

$\begin{array}{c}f\left(53.1760\right)=1.2\left(75000e^{-0.045\left(53.1760\right)}+100000\right)-\frac{300000}{1+29e^{-0.08\left(53.1760\right)}}\\ =-84245\end{array}$

As $f\left(0\right)f\left(53.1760\right)<0$, the root lies in the interval.

Now proceed with the second iteration as follows,

$\begin{array}{c}{x}_2=f\left(0\right)-\frac{\left(53.1760-0\right)f\left(53.1760\right)}{f\left(53.1760\right)-f\left(0\right)}\\ =37.4156\end{array}$

The relative approximate percentage error is,

$\begin{array}{c}{\epsilon }_a=\left(\frac{\left|x_2-x_1\right|}{x_2}\times 100\right)\%\\ =42.123\%\end{array}$

Continue with the same process till the relative approximate percentage error is less that 0.1%.

Use the following MATLAB code to implement false-position method and solve for the roots iteratively as,

% Q 8-23P part (b)

functionfalse_posn()

% Upper bound

t1=100;

f1=myfunc(t1);

% Lower bound

t2=0;

f2=myfunc(t2);

% Starting error could be anything

err=1;

% Introduce the tolerace provided as 0.01%

tol=1e-4;

while err>tol

fori=1:5

% The formula for the secant rule

tr(i)=t2-f2*(t1-t2)/(f1-f2);

fr(i)=myfunc(tr(i));

% Changing interval

if sign(fr(i))==sign(f1)

t1=tr(i);

f1=fr(i);

else t2=tr(i);

f2=fr(i);

end

end

fori=1:4

% Error bound

err(i)=abs((tr(i+1)-tr(i))/tr(i+1));

end

end

tr

err

t1

t2

end

function out=myfunc(t)

out=1.2*(75000*exp(-0.045*t)+100000)-300000/(1+29*exp(-0.08*t));

end

Execute the above code to obtain the solutions tabulated as,

$\begin{array}{ccccc}i& a& b& x_i& {\epsilon }_a\\ 1& 0& 100& 53.176& -\\ 2& 0& 53.176& 37.4156& 42.123\%\\ 3& 37.4156& 53.176& 39.7221& 5.807\%\\ 4& 37.4156& 39.7221& 39.6063& 0.292\%\\ 5& 39.6063& 39.7221& 39.6068& 0.001\%\end{array}$

The process is stopped at the fifth iteration where the relative approximate percentage error is less than 0.1%. This gives the value of t as 39.6068 years.

Substitute 39.6068 for t in the formula for the urban population to get,

$\begin{array}{c}{P}_u\left(t\right)=75000e^{-0.045\left(39.6068\right)}+100000\\ \approx 112,618.7\end{array}$

Hence, the urban population after 39.6068 years is $112618.7$.

Substitute 39.6068 for t in the formula for the suburban population to get,

$\begin{array}{c}{P}_s\left(t\right)=\frac{300000}{1+29e^{-0.08\left(39.6068\right)}}\\ \approx 135142.5\end{array}$

Hence, the suburban population after 39.6068 years is $135142.5$.

To determine

To calculate: The values of the urban and sub-urban population and the time where the urban population is given by the formula $P_u\left(t\right)=P_{u,\max }{e}^{-k_{u}t}+P_{u,\min }$ and the sub-urban population is given by the formula $P_s\left(t\right)=\frac{P_{s,\max }}{1+\left[\frac{P_{s,\max }}{P_0}-1\right]e^{-k_{s}t}}$ for the parameters $P_{u,\max }=75000$, $P_{u,\min }=100000$, $k_u=0.045,k_s=0.08,P_{S,\max }=300000$, and $P_0=10000$ using the modified secant method with the additional information that at time t, the suburbs are 20% larger than the city.

Answer to Problem 23P

Solution: After 39.6068 years, the suburban population would be 1.2 times the urban population with the populations of the suburban and urban areas being 13 5142.5 and 112 618.7, respectively.

Explanation of Solution

Given Information:

The expression, $P_u\left(t\right)=P_{u,\max }{e}^{-k_{u}t}+P_{u,\min }$ and $P_s\left(t\right)=\frac{P_{s,\max }}{1+\left[\frac{P_{s,\max }}{P_0}-1\right]e^{-k_{s}t}}$ for the parameters $P_{u,\max }=75000$, $P_{u,\min }=100000$, $k_u=0.045,k_s=0.08,P_{S,\max }=300000$, and $P_0=10000$ where the suburbs are 20% larger than the city at time t.

Formula used:

An equation $f\left(x\right)=0$ can be solved by the modified scant method over the interval $\left[a,b\right]$ using the iterative formula,

Step 1: Let $x_0=\frac{a+b}{2}$.

Step 2: Compute $x_{i+1}=x_i-\frac{f\left(x_i\right)}{f\text{'}\left(x_i\right)}$ where $f\text{'}\left(x_i\right)=\frac{f\left(x_i+x_{i}h\right)-f\left(x_i\right)}{x_{i}h}$.

Step 3: Proceed with the same process till ${\epsilon }_a<{\epsilon }_s$.

Calculation:

Substitute 75000 for $P_{u,\max }$, 100000 for $P_{u,\min }$, and $0.045$ for $k_u$ in the formula for the urban population to obtain,

$P_u\left(t\right)=75000e^{-0.045t}+100000$

Substitute 300000 for $P_{s,\max }$, 10000 for $P_0$, and 0.08 for $k_s$ in the formula for the suburban population to obtain,

$\begin{array}{c}{P}_s\left(t\right)=\frac{300000}{1+\left[\frac{300000}{10000}-1\right]e^{-0.08t}}\\ P_s\left(t\right)=\frac{300000}{1+29e^{-0.08t}}\end{array}$

It has been provided that at time t, the suburban population is 20% larger than the urban population, that is, 1.2 times the urban population. Thus,

$1.2\left(75000e^{-0.045t}+100000\right)=\frac{300000}{1+29e^{-0.08t}}$

The above equation can be rewritten in the form of a following function whose zero corresponds with the root of the equation.

$f\left(t\right)=1.2\left(75000e^{-0.045t}+100000\right)-\frac{300000}{1+29e^{-0.08t}}$

The desired value of t can be found using the modified secant method.

Let the initial guess be 50 and the value of h be 0.01.

Then,

$\begin{array}{c}f\left(50\right)=1.2\left(75000e^{-0.045\left(50\right)}+100000\right)-\frac{300000}{1+29e^{-0.08\left(50\right)}}\\ =-66444.8\\ f\left(50+0.01\cdot 50\right)=1.2\left(75000e^{-0.045\left(50.5\right)}+100000\right)-\frac{300000}{1+29e^{-0.08\left(50.5\right)}}\\ f\left(50.5\right)=-69357.6\end{array}$

And,

$\begin{array}{c}f\text{'}\left(50\right)=\frac{f\left(50.5\right)-f\left(50\right)}{0.5}\\ =-5825.72\end{array}$

Now proceed with the first iteration as follows:

$\begin{array}{c}{x}_1=50-\frac{f\left(50\right)}{f\text{'}\left(50\right)}\\ =38.5946\end{array}$

Further,

$\begin{array}{c}f\left(38.5946\right)=1.2\left(75000e^{-0.045\left(38.5946\right)}+100000\right)-\frac{300000}{1+29e^{-0.08\left(38.5946\right)}}\\ =6692.132\\ f\left(38.5946+0.01\cdot 38.5946\right)=1.2\left(75000e^{-0.045\left(38.98053\right)}+100000\right)-\frac{300000}{1+29e^{-0.08\left(38.98053\right)}}\\ f\left(38.98053\right)=4143.604\end{array}$

And,

$\begin{array}{c}f\text{'}\left(38.5946\right)=\frac{f\left(38.98053\right)-f\left(3835946\right)}{0.38595}\\ =-6603.33\end{array}$

Now proceed with the second iteration as follows:

$\begin{array}{c}{x}_2=38.5946-\frac{f\left(38.5946\right)}{f\text{'}\left(38.5946\right)}\\ =39.6080\end{array}$

The relative approximate percentage error is,

$\begin{array}{c}{\epsilon }_a=\left(\frac{\left|x_2-x_1\right|}{x_2}\times 100\right)\%\\ =29.552\%\end{array}$

Continue with the same process till the relative approximate percentage error is less that 0.1%.

Use the following MATLAB code to implement modified secant method and solve for the roots iteratively as,

% Q 8-23P (c)

function[xr, approx_err]=secant(xr, tol, h, maxit)

% Set the values

ifnargin<5, maxit=50;end

ifnargin<4, tol=0.001;end

iteration=0;

while (1)

% Formula for modified secant method

xrnew=xr-h*xr*g(xr)/((g(xr+h*xr)-g(xr)));

iteration=iteration+1;

ifxrnew~=0

% Calculate the error

ea=abs((xrnew-xr)/xrnew)*100;

end

approx_err(iteration)=ea;

% Break the program if error exceeds tolerance or maximum iterations

% are reached

ifea<=tol||iteration>=maxit

break;

end

xrold=xr;

xr=xrnew;

end

end

% Define the equation

function out=g(t)

out=1.2*(75000*exp(-0.045*t)+100000)-300000/(1+29*exp(-0.08*t));

end

Execute the above code to obtain the solutions tabulated as,

$\begin{array}{ccc}i& t_i& {\epsilon }_a\\ 0& 50& -\\ 1& 38.5946& 29.552\%\\ 2& 39.6080& 2.559\%\\ 3& 39.6068& 0.003\%\end{array}$

The process is stopped at the third iteration where the relative approximate percentage error is less that 0.1%. This gives the value of t as 39.6068 years.

Substitute 39.6068 for t in the formula for the urban population to get,

$\begin{array}{c}{P}_u\left(t\right)=75000e^{-0.045\left(39.6068\right)}+100000\\ \approx 112,618.7\end{array}$

Hence, the urban population after 39.6068 years is $112618.7$.

Substitute 39.6068 for t in the formula for the suburban population to get:

$\begin{array}{c}{P}_s\left(t\right)=\frac{300000}{1+29e^{-0.08\left(39.6068\right)}}\\ \approx 135142.5\end{array}$

Hence, the suburban population after 39.6068 years is $135142.5$.