1 Introduction, Measurement, Estimating 2 Describing Motion: Kinematics In One Dimension 3 Kinematics In Two Or Three Dimensions; Vectors 4 Dynamics: Newton's Laws Of Motion 5 Using Newton's Laws: Friction, Circular Motion, Drag Forces 6 Gravitation And Newton's Synthesis 7 Work And Energy 8 Conservation Of Energy 9 Linear Momentum 10 Rotationalmotion 11 Angular Momentum; General Rotation 12 Static Equilibrium; Elasticity And Fracture 13 Fluids 14 Oscillations 15 Wave Motion 16 Sound 17 Temperature, Thermal Expansion And The Ideal Gas Law 18 Kinetic Theory Of Gases 19 Heat And The First Law Of Thermodynamics 20 Second Law Of Thermodynamics 21 Electric Charge And Electric Field 22 Gauss's Law 23 Electric Potential 24 Capacitance, Dielectrics, Electric Energy Storage 25 Electric Currents And Resistance 26 Dc Circuits 27 Magnetism 28 Sources Of Magnetic Field 29 Electromagnetic Induction And Faraday's Law 30 Inductance, Electromagnetic Oscillations, And Ac Circuits 31 Maxwell's Equation And Electromagnetic Waves 32 Light: Reflection And Refraction 33 Lenses And Optical Instruments 34 The Wave Nature Of Light: Interference 35 Diffraction And Polarization 36 Special Theory Of Relativity 37 Early Quantum Theory And Models Of The Atom 38 Quantum Mechanics 39 Quantum Mechanics Of Atoms 40 Molecules And Solids 41 Nuclear Physics And Radioactivity 42 Nuclear Energy; Effects And Uses Of Radiation 43 Elementary Particles 44 Astrophysics And Cosmology expand_more
7.1 Work Done By A Constant Force 7.2 Scalar Product Of Two Vectors 7.3 Work Done By A Varying Force 7.4 Kinetic Energy And The Work-energy Principle Chapter Questions expand_more
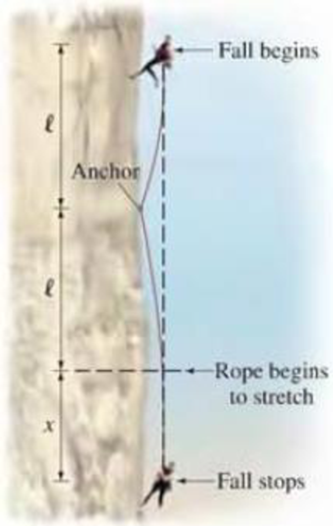
Problem 1Q: In what ways is the word work as used in everyday language the same as defined in physics? In what... Problem 2Q: A woman swimming upstream is not moving with respect to the shore. Is she doing any work? If she... Problem 3Q: Can a centripetal force ever do work on an object? Explain. Problem 4Q: Why is it tiring to push hard against a solid wall even though you are doing no work? Problem 5Q: Does the scalar product of two vectors depend on the choice of coordinate system? Problem 6Q: Can a dot product ever he negative? If yes, under what conditions? Problem 7Q Problem 8Q: Does the dot product of two vectors have direction as well as magnitude? Problem 9Q: Can the normal force on an object ever do work? Explain. Problem 10Q: You have two springs that are identical except that spring 1 is stiffer than spring 2 (k1 k2). On... Problem 11Q Problem 12Q: In Example 710, it was stated that the block separates from the compressed spring when the spring... Problem 13Q: Two bullets are fired at the same time with the same kinetic energy. If one bullet has twice the... Problem 14Q: Does the net work done on a particle depend on the choice of reference frame? How does this affect... Problem 15Q: A hand exerts a constant horizontal force on a block that is free to slide on a frictionless surface... Problem 1P: (I) How much work is done by the gravitational force when a 280-kg pile driver falls 2.80 m? Problem 2P: (I) How high will a 1.85-kg rock go if thrown straight up by someone who does 80.0 J of work on it?... Problem 3P: (I) A 75.0-kg firefighter climbs a flight of stairs 20.0 m high. How much work is required? Problem 4P: (I) A hammerhead with a mass of 2.0 kg is allowed to fall onto a nail from a height of 0.50 m. What... Problem 5P: (II) Estimate the work you do to mow a lawn 10 m by 20 m with a 50-cm wide mower. Assume you push... Problem 6P: (II) A lever such as that shown in Fig. 720 can be used to lift objects we might not otherwise be... Problem 7P: (II) What is the minimum work needed to push a 950-kg car 1310 m up along a 9.0 incline? Ignore... Problem 8P: (II) Eight books, each 4.0cm thick with mass 1.8 kg, lie flat on a table. How much work is required... Problem 9P: (II) A box of mass 6.0 kg is accelerated from rest by a force across a floor at a rate of 2.0 m/s2... Problem 10P: (II) (a) What magnitude force is required to give a helicopter of mass M an acceleration of 0.10 g... Problem 11P: (II) A 380-kg piano slides 3.9m down a 27 incline and is kept from accelerating by a man who is... Problem 12P: (II) A gondola can carry 20 skiers, with a total mass of up to 2250 kg. The gondola ascends at a... Problem 13P: (II) A 17,000-kg jet takes off from an aircraft carrier via a catapult (Fig. 722a). The gases thrust... Problem 14P: (II) A 2200-N crate rests on the floor. How much work is required to move it at constant speed (a)... Problem 15P: (II) A grocery cart with mass of 16 kg is being pushed at constant speed up a flat 12 ramp by a... Problem 16P: (I) What is the dot product of A=2.0x2i4.0xj+5.0kandB=11.0i+2.5xj? Problem 17P: (I) For any vector V=Vxi+Vyj+Vzk show that Vx=iV,Vy=jV,Vz=kV. Problem 18P: (I) Calculate the angle between the vectors: A=6.8i3.4j6.2k and B=8.2i+2.3j7.0k. Problem 19P Problem 20P: (I) Vector V1 points along the z axis and has magnitude V1 = 75. Vector V2 lies in the xz plane, has... Problem 21P: (II) Given the vector A=3.0i+1.5j, find a vector Bthat is perpendicular to A Problem 22P: (II) A constant force F=(2.0i+4.0j)N acts on an object as it moves along a straight-line path. If... Problem 23P: (II) If A=9.0i8.5j,B=8.0i+7.1j+4.2k,and C=6.8i9.2j,determine (a) A(B+C); (b) (A+C)B; (c) (B+A)C. Problem 24P: (II) Prove that AB=AxBx+AyBy+AzBz, starting from Eq. 72 and using the distributive property (p.... Problem 25P: (II) Given vectors A=4.8i+6.8jandB=9.6i+6.7j, determine the vector C that lies in the xy plane... Problem 26P: (II) Show that if two nonparallel vectors have the same magnitude, their sum must he perpendicular... Problem 27P: (II) Let V=20.0i+22.0j14.0k. What angles does this vector make with the x, y, and z axes? Problem 28P: (II) Use the scalar product to prove the law of cosines for a triangle: c2=a2+b22abcos. where a, b,... Problem 29P: (II) Vectors A and B are in the xy plane and their scalar product is 20.0 units. If A makes a 27.4... Problem 30P: (II) A and B are two vectors in the xy plane that make angles and with the x axis respectively.... Problem 31P: (II) Suppose A=1.0i+1.0j2.0k and B=1.0i+1.0j+2.0k, (a) what is the angle between these two vectors?... Problem 32P: (II) Find a vector of unit length in the xy plane that is perpendicular to 3.0i + 4.0j. Problem 33P: (III) Show that the scalar product of two vectors is distributive: A(B+C)=AB+AC. [Hint: Use a... Problem 34P: (I) In pedaling a bicycle uphill, a cyclist exerts a downward force of 450 N during each stroke. If... Problem 35P: (II) A spring has k = 65N/m. Draw a graph like that inFig. 711 and use it to determine the work... Problem 36P: (II) If the hill in Example 72 (Fig. 74) was not an evenslope hut rather an irregular curve as in... Problem 37P: (II) The net force exerted on a particle acts in the positivex direction. Its magnitude increases... Problem 38P: (II) If it requires 5.0 J of work to stretch a particular spring by 2.0 cm from its equilibrium... Problem 39P: (II) In Fig. 79 assume the distance axis is the x axis and that a = 10.0 m and b = 30.0 m. Estimate... Problem 40P: (II) The force on a particle, acting along the x axis, varies as shown in Fig. 724. Determine the... Problem 41P: (II) A child is pulling a wagon down the sidewalk. For 9.0 m the wagon stays on the sidewalk and the... Problem 42P: (II) The resistance of a packing material to a sharp object penetrating it is a force proportional... Problem 43P: (II) The force needed to hold a particular spring compressed an amount x from its normal length is... Problem 44P: (II) At the top of a pole vault, and athlete actually can do work pushing on the pole before... Problem 45P: (II) Consider a force F1=A/xwhich acts on an object during its journey along the x axis from x = 0.0... Problem 46P: (II) Assume that a force acting on an object is given by F=axi+byj, where the constants a = 3.0 Nm1... Problem 47P: (II) An object, moving along the circumference of a circle with radius R, is acted upon by a force... Problem 48P: (III) A 2800-kg space vehicle, initially at rest, falls vertically from a height of 3300 km above... Problem 49P: (III) A 3.0-m-long steel chain is stretched out along the top level of a horizontal scaffold at a... Problem 50P: (I) At room temperature, an oxygen molecule, with mass of 5.31 10-26 kg, typically has a kinetic... Problem 51P: (I) (a) If the kinetic energy of a particle is tripled, by what factor has its speed increased? (b)... Problem 52P: (I) How much work is required to stop an electron (m = 9.11 1031 kg) which is moving with a speed... Problem 53P: (I) How much work must be done to stop a 1300-kg car traveling at 95 km/h? Problem 54P: (II) Spiderman uses his spider webs to save a runaway train, Fig. 727. His web stretches a few city... Problem 55P: (II) A baseball (m=145g) traveling 32mA moves a fielder's glove backward 25 cm when the ball is... Problem 56P: (II) An 85-g arrow is fired from a bow whose string exerts an average force of 105 N on the arrow... Problem 57P: (II) A mass m is attached to a spring which is held stretched a distance x by a force F (Fig. 728),... Problem 58P: (II) If the speed of a car is increased by 50%, by what factor will its minimum braking distance be... Problem 59P: (II) A 1200-kg car rolling on a horizontal surface has speed v = 66 km/h when it strikes a... Problem 60P: (II) One car has twice the mass of a second car, but only half as much kinetic energy. When both... Problem 61P: (II) A 4.5-kg object moving in two dimensions initially has avelocity v1=(10.0i+20.0j)m/s. A net... Problem 62P: (II) A 265-kg load is lifted 23.0m vertically with an acceleration a = 0.150 g by a single cable.... Problem 63P: (II) (a) How much work is done by the horizontal force Fp=150N on the 18-kg block of Fig. 729 when... Problem 64P: (II) (a) How much work is done by the horizontal force Fp = 150 N on the 18-kg block of Fig. 729... Problem 65P: (II) At an accident scene on a level road, investigators measure a cars skid mark to be 98 m long.... Problem 66P: (II) A 46.0-kg crate, starting from rest, is pulled across a floor with a constant horizontal force... Problem 67P: (II) A train is moving along a track with constant speed 1 relative to the ground. A person on the... Problem 68P: (III) We usually neglect the mass of a spring if it is small compared to the truss attached to it.... Problem 69P: (III) An elevator cable breaks when a 925-kg elevator is 22.5 m above the top of a huge spring (k =... Problem 70GP: (a) A 3.0-g locust reaches a speed of 3.0m/s during its jump. What is its kinetic energy at this... Problem 71GP: In a certain library the first shelf is 12.0 cm off the ground, and the remaining 4 shelves are each... Problem 72GP: A 75-kg meteorite buries itself 5.0 m into soft mud. The force between the meteorite and the mud is... Problem 73GP: A 6.10-kg block is pushed 9.25 m up a smooth 37.0 inclined plane by a horizontal force of 75.0 N. If... Problem 74GP Problem 75GP: Two forces, F1=(1.50i0.80j+0.70k)Nand F2=(0.70i+1.20j)N, are applied on a moving object of mass0.20... Problem 76GP: The barrels of the 16-in, guns (bore diameter = 16 in. = 41cm) on the World War II battleship U.S.S.... Problem 77GP: A varying force is given by F = Aekx, where x is the position: A and k are constants that have units... Problem 78GP: The force required to compress an imperfect horizontal spring an amount x is given by F = 150x +... Problem 79GP: A force F=(10.0i+9.0j+12.0k)kNacts on a small object of mass 95 g. If the displacement of the object... Problem 80GP: In the game of paintball, players use guns powered by pressurized gas to propel 33-g gel capsules... Problem 81GP: A softball having a mass of 0.25 kg is pitched horizontally at 110 km/h. By the time it reaches the... Problem 82GP: An airplane pilot fell 370 m after jumping from an aircraft without his parachute opening. He landed... Problem 83GP: Many cars have 5 mi/h (8 km/h) bumpers that are designed to compress and rebound elastically without... Problem 84GP: What should be the spring constant k of a spring designed to bring a 1300-kg car to rest from a... Problem 85GP: Assume a cyclist of weight mg can exert a force on the pedals equal to 0.90 mg on the average. If... Problem 86GP: A simple pendulum consists of a small object of mass m (the bob) suspended by a cord of length ... Problem 87GP: A car passenger buckles himself in with a seat belt and holds his 18-kg toddler on his lap. Use the... Problem 88GP: As an object moves along the x axis from x = 0.0 m to x = 20.0 m it is acted upon by a force given... Problem 89GP: A cyclist starts from rest and coasts down a 4.0 hill.The mass of the cyclist plus bicycle is 85 kg.... Problem 90GP: Stretchable ropes ate used to safely arrest the fall of rock climbers. Suppose one end of a rope... Problem 91GP: A small mass m hangs at rest from a vertical rope of length that is fixed to the ceiling. A force... Problem 92GP: (II) The net force along the linear path of a panicle of mass 480 g has been measured at 10.0-cm... Problem 93GP: (II) When different masses are suspended from a spring the spring stretches by different amounts as... format_list_bulleted


 Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning




