MYLAB MATH FOR EXCURSIONS IN MATHEMATIC
9th Edition
ISBN: 9780136415893
Author: Tannenbaum
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 7, Problem 7E
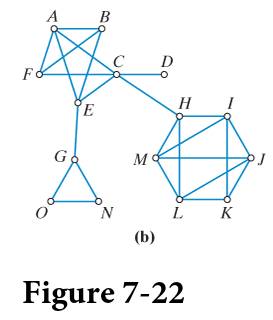
Consider the network shown in.
a. In addition to the pair
b. If you can, find two vertices in the network having seven degrees of separation between them. If you can’t, then briefly explain why you don’t think there are any.
c. What is the diameter of the network?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The following are suggested designs for group sequential studies. Using PROCSEQDESIGN, provide the following for the design O’Brien Fleming and Pocock.• The critical boundary values for each analysis of the data• The expected sample sizes at each interim analysisAssume the standardized Z score method for calculating boundaries.Investigators are evaluating the success rate of a novel drug for treating a certain type ofbacterial wound infection. Since no existing treatment exists, they have planned a one-armstudy. They wish to test whether the success rate of the drug is better than 50%, whichthey have defined as the null success rate. Preliminary testing has estimated the successrate of the drug at 55%. The investigators are eager to get the drug into production andwould like to plan for 9 interim analyses (10 analyzes in total) of the data. Assume thesignificance level is 5% and power is 90%.Besides, draw a combined boundary plot (OBF, POC, and HP)
4. Solve the system of equations and express your solution using vectors.
2x1 +5x2+x3 + 3x4 = 9
-x2+x3 + x4 = 1
-x1-6x2+3x3 + 2x4
= -1
3. Simplify the matrix expression
A(A-B) - (A+B)B-2(A - B)2 + (A + B) 2
Chapter 7 Solutions
MYLAB MATH FOR EXCURSIONS IN MATHEMATIC
Ch. 7 - A computer lab has seven computers labeled A...Ch. 7 - The following is a list of the electrical power...Ch. 7 - Consider the network shown in Fig.720_. a. How...Ch. 7 - Consider the network shown in Fig.721_. a. How...Ch. 7 - Consider once again the network shown in. Fig720_....Ch. 7 - Consider once again the network shown in. Fig721_....Ch. 7 - Consider the network shown in. Fig722. This is the...Ch. 7 - Consider the network shown in. Fig723_. This is...Ch. 7 - Consider the tree shown in. Fig724_. a. How many...Ch. 7 - Consider the tree shown in. Fig725. a. How many...
Ch. 7 - In Exercises 11 through 24 you are given...Ch. 7 - Prob. 12ECh. 7 - Prob. 13ECh. 7 - Prob. 14ECh. 7 - In Exercises 11 through 24 you are given...Ch. 7 - Prob. 16ECh. 7 - Prob. 17ECh. 7 - Prob. 18ECh. 7 - Prob. 19ECh. 7 - In Exercises 11 through 24 you are given...Ch. 7 - Prob. 21ECh. 7 - Prob. 22ECh. 7 - Prob. 23ECh. 7 - Prob. 24ECh. 7 - Prob. 25ECh. 7 - Consider the network shown in Fig.727_. a. Find a...Ch. 7 - Prob. 27ECh. 7 - Consider the network shown in Fig.729_. a. Find a...Ch. 7 - Prob. 29ECh. 7 - Prob. 30ECh. 7 - Prob. 31ECh. 7 - Prob. 32ECh. 7 - Prob. 33ECh. 7 - Prob. 34ECh. 7 - Prob. 35ECh. 7 - The 4 by 5 grid shown in Fig. 7-37 represents a...Ch. 7 - Prob. 37ECh. 7 - Find the MST of the network shown in Fig. 7-39...Ch. 7 - Find the MST of the network shown in Fig. 7-40...Ch. 7 - Find the MST of the network shown in Fig. 7-41...Ch. 7 - Prob. 41ECh. 7 - Find the MaxST of the network shown in Fig. 7-39...Ch. 7 - Find the MaxST of the network shown in Fig. 7-40...Ch. 7 - Prob. 44ECh. 7 - The mileage chart in Fig. 742 shows the distances...Ch. 7 - Figure 7-43a shows a network of roads connecting...Ch. 7 - Prob. 47ECh. 7 - Prob. 48ECh. 7 - Prob. 49ECh. 7 - This exercise refers to weighted networks where...Ch. 7 - Prob. 51ECh. 7 - Prob. 52ECh. 7 - Prob. 53ECh. 7 - Prob. 54ECh. 7 - Prob. 55ECh. 7 - Prob. 56ECh. 7 - A bipartite graph is a graph with the property...Ch. 7 - Prob. 58ECh. 7 - Prob. 59E
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 10 5 Obtain by multiplying matrices the composite coordinate transformation of two transformations, first x' = (x + y√√2+2)/2 y' = z' (x√√2-2√2)/2 z = (-x+y√√2-2)/2 followed by x" = (x'√√2+z'√√2)/2 y" = (-x'y'√√2+2')/2 z" = (x'y'√√2-2')/2.arrow_forwardNot use ai pleasearrow_forward4 The plane 2x+3y+ 6z = 6 intersects the coordinate axes at P, Q, and R, forming a triangle. Draw a figure and identify the three points on it. Also find vectors PQ and PR. Write a vector formula for the area of the triangle PQR and find its value.arrow_forward
- 3.1 Limits 1. If lim f(x)=-6 and lim f(x)=5, then lim f(x). Explain your choice. x+3° x+3* x+3 (a) Is 5 (c) Does not exist (b) is 6 (d) is infinitearrow_forward1 pts Let F and G be vector fields such that ▼ × F(0, 0, 0) = (0.76, -9.78, 3.29), G(0, 0, 0) = (−3.99, 6.15, 2.94), and G is irrotational. Then sin(5V (F × G)) at (0, 0, 0) is Question 1 -0.246 0.072 -0.934 0.478 -0.914 -0.855 0.710 0.262 .arrow_forwardAnswer the number questions with the following answers +/- 2 sqrt(2) +/- i sqrt(6) (-3 +/-3 i sqrt(3))/4 +/-1 +/- sqrt(6) +/- 2/3 sqrt(3) 4 -3 +/- 3 i sqrt(3)arrow_forward
- 2. Answer the following questions. (A) [50%] Given the vector field F(x, y, z) = (x²y, e", yz²), verify the differential identity Vx (VF) V(V •F) - V²F (B) [50%] Remark. You are confined to use the differential identities. Let u and v be scalar fields, and F be a vector field given by F = (Vu) x (Vv) (i) Show that F is solenoidal (or incompressible). (ii) Show that G = (uvv – vVu) is a vector potential for F.arrow_forwardA driver is traveling along a straight road when a buffalo runs into the street. This driver has a reaction time of 0.75 seconds. When the driver sees the buffalo he is traveling at 44 ft/s, his car can decelerate at 2 ft/s^2 when the brakes are applied. What is the stopping distance between when the driver first saw the buffalo, to when the car stops.arrow_forwardTopic 2 Evaluate S x dx, using u-substitution. Then find the integral using 1-x2 trigonometric substitution. Discuss the results! Topic 3 Explain what an elementary anti-derivative is. Then consider the following ex integrals: fed dx x 1 Sdx In x Joseph Liouville proved that the first integral does not have an elementary anti- derivative Use this fact to prove that the second integral does not have an elementary anti-derivative. (hint: use an appropriate u-substitution!)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Minimum cuts and maximum flow rate; Author: Juddy Productions;https://www.youtube.com/watch?v=ylxhl1ipWss;License: Standard YouTube License, CC-BY