Concept explainers
Videos
A computer lab has seven computers labeled A through G. The connections between computers are as follows:
•
•
•
•
•
•
•
Is the lab set-up a computer network? Explain why or why not.
To check:
Whether the lab set-up is a computer network or not.
Answer to Problem 1E
Solution:
The lab set-up is not a computer network.
Explanation of Solution
Given:
A computer lab has seven computers labeled A through G. The connections between computers are as follows:
•
•
•
•
•
•
•
Approach:
A network is a connected graph in which there is a path going from one vertex to any other vertex.
Calculation:
Draw a graph of the connections between the computers. Connect computer
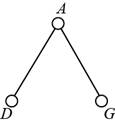
Figure (1)
Connect computer
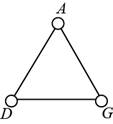
Figure (2)
Draw nodes for computers
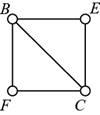
Figure (3)
By combining both, the following graph is obtained.
Figure (4)
From figure (4), there are two separate components in the graph and there is no path from one component to the other. Therefore the lab set-up is not a computer network.
Conclusion:
Thus, the lab set-up is not a computer network.
Want to see more full solutions like this?
Chapter 7 Solutions
MYLAB MATH FOR EXCURSIONS IN MATHEMATIC
Additional Math Textbook Solutions
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
Pathways To Math Literacy (looseleaf)
Precalculus: Mathematics for Calculus (Standalone Book)
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Precalculus
College Algebra (7th Edition)
- ANBNC ND B こ Ꭰarrow_forward1 Matching 10 points Factor and Solve 1)x3-216 0, x = {6,[B]} 2) 16x3 = 54 x-[3/2,[D]] 3)x4x2-42 0 x= [ +/-isqrt(7), [F] } 4)x+3-13-9x x=[+/-1.[H]] 5)x38x2+16x=0, x = {0,[K}} 6) 2x6-10x-48x2-0 x-[0, [M], +/-isqrt(3)) 7) 3x+2x²-8 x = {+/-i sqrt(2), {Q}} 8) 5x³-3x²+32x=2x+18 x = {3/5, [S]} [B] [D] [F] [H] [K] [M] [Q] +/-2 sqrt(2) +/- i sqrt(6) (-3+/-3 i sqrt(3))/4 +/- 1 +/-sqrt(6) +/- 2/3 sqrt(3) 4 -3 +/- 3 i sqrt(3) [S]arrow_forwardD U(AUBUC) B Darrow_forward
- helparrow_forwardAnswer question 2.28 please.arrow_forwardQuestion 2 Let F be a solenoidal vector field, suppose V × F = (-8xy + 12z², −9x² + 4y² + 9z², 6y²), and let (P,Q,R) = V²F(.725, —.283, 1.73). Then the value of sin(2P) + sin(3Q) + sin(4R) is -2.024 1.391 0.186 -0.994 -2.053 -0.647 -0.588 -1.851 1 ptsarrow_forward
- I just need b,c,darrow_forward1 pts Let F and G be vector fields such that ▼ × F(0, 0, 0) = (0.76, -9.78, 3.29), G(0, 0, 0) = (−3.99, 6.15, 2.94), and G is irrotational. Then sin(5V (F × G)) at (0, 0, 0) is Question 1 -0.246 0.072 -0.934 0.478 -0.914 -0.855 0.710 0.262 .arrow_forward8. In the following check to see if the set S is a vector subspace of the corresponding Rn. If it is not, explain why not. If it is, then find a basis and the dimension. X1 (a) S = X2 {[2], n ≤ n } c X1 X2 CR² X1 (b) S X2 = X3 X4 x1 + x2 x3 = 0arrow_forward
- Par quel quadrilatère est-elle représentée sur ce besoin en perspective cavalièrearrow_forwardPlease provide the solution for the attached image in detailed.arrow_forward5 Obtain by multiplying matrices the composite coordinate transformation of two transformations, first x' = (x + y√2+ z)/2 followed by y' = (x√√2-2√2)/2 z' = (-x+y√2-2)/2 x" = y" 2" = (x'√√2+2'√√2)/2 (-x'y'√√2+)/2 (x'y' √√2-z)/2.arrow_forward
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt