Chapter 7, Problem 7.4P

To determine

(a)

Value of H on the z -axis.

Answer to Problem 7.4P

   $H_{Total}=\frac{I{a}^2}{2}\left(\frac{1}{{\left(a^2+{\left(z-h\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(a^2+{\left(z+h\right)}^2\right)}^{\frac{3}{2}}}\right)a_z$

Explanation of Solution

Given:

The given configuration is

I = $1\text{A}$

Range is $-h<z<h$.

Calculation:

The figure for the loop structures carrying current can be drawn as below:

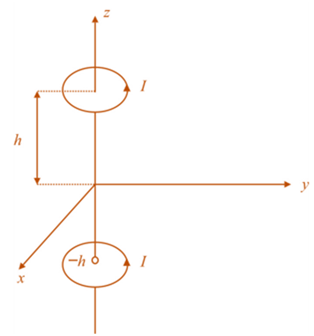
The equation for H because of small current element 'Idl' will be

   $dH=\frac{Idl\left(a_{\varphi }\right)\times a_{R1P}}{4\pi R_{1p}^2}$

The vector starting from current loop to the concerned point at a height 'h' will be

   $a_{R1P}=\frac{-a{a}_{\rho }-\left(h-z\right)a_z}{\sqrt{a^2+{\left(z-h\right)}^2}}$

The differential expression for magnetic field intensity will be

   $\begin{array}{l}d{H}_1=\frac{Idl\times \frac{\left(-a{a}_{\rho }-\left(z-h\right)a_z\right)}{\sqrt{a^2+{\left(z-h\right)}^2}}}{4\pi {\left(\sqrt{a^2+{\left(z-h\right)}^2}\right)}^2}\\ d{H}_1=\frac{Iad\varphi a_{\varphi }\times \left(-a{a}_{\rho }-\left(z-h\right)a_z\right)}{4\pi {\left(a^2+{\left(z-h\right)}^2\right)}^{\frac{3}{2}}}\\ d{H}_1=\frac{Iad\varphi \times \left(a{a}_z-\left(z-h\right)a_{\rho }\right)}{4\pi {\left(a^2+{\left(z-h\right)}^2\right)}^{\frac{3}{2}}}\end{array}$

The vector starting from current loop to the concerned point at a height 'h' will be

   $a_{R2P}=\frac{-a{a}_{\rho }-\left(z+h\right)a_z}{\sqrt{a^2+{\left(z+h\right)}^2}}$

The equation for H because of small current element 'Idl' will be

   $dH=\frac{Idl\left(a_{\varphi }\right)\times a_{R2P}}{4\pi R_{2p}^2}$

The differential expression for magnetic field intensity will be

   $\begin{array}{l}d{H}_2=\frac{Idl\times \frac{\left(-a{a}_{\rho }-\left(z+h\right)a_z\right)}{\sqrt{a^2+{\left(z+h\right)}^2}}}{4\pi {\left(\sqrt{a^2+{\left(z+h\right)}^2}\right)}^2}\\ d{H}_2=\frac{Iad\varphi a_{\varphi }\times \left(-a{a}_{\rho }+\left(z+h\right)a_z\right)}{4\pi {\left(a^2+{\left(z+h\right)}^2\right)}^{\frac{3}{2}}}\\ d{H}_2=\frac{Iad\varphi \times \left(a{a}_z+\left(z+h\right)a_{\rho }\right)}{4\pi {\left(a^2+{\left(z+h\right)}^2\right)}^{\frac{3}{2}}}\end{array}$

Because of symmetry, the magnetic field is there only in the direction of $a_z$ . That is why, $a_{\rho }$ components are neglected. The resultant expressions will be

   $\begin{array}{l}d{H}_1=\frac{Iad\varphi \left(\rho a_z\right)}{4\pi {\left(a^2+z^2\right)}^{\frac{3}{2}}}\\ d{H}_2=\frac{Iad\varphi \left(a{a}_z\right)}{4\pi {\left(a^2+{\left(z+h\right)}^2\right)}^{\frac{3}{2}}}\end{array}$

Integrating over an azimuthal angle $2\pi$

   ${\displaystyle \underset{0}{\overset{2\pi }{\int }}dH}={\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{I\rho d\varphi \left(a{a}_z-z{a}_{\rho }\right)}{4\pi {\left(a^2+z^2\right)}^{\frac{3}{2}}}}$

The total magnetic field due to upper ring will be

   $\begin{array}{l}{H}_1={\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{Iad\varphi \left(a{a}_z\right)}{4\pi {\left(a^2+{\left(z-h\right)}^2\right)}^{\frac{3}{2}}}}\\ H_1=\frac{Ia\left(a{a}_z\right)}{4\pi {\left(a^2+{\left(z-h\right)}^2\right)}^{\frac{3}{2}}}{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\varphi }\\ H_1=\frac{Ia\left(a{a}_z\right)}{4\pi {\left(a^2+{\left(z-h\right)}^2\right)}^{\frac{3}{2}}}\left[2\pi \right]\\ H_1=\frac{I{a}^2{a}_z}{2{\left(a^2+{\left(z-h\right)}^2\right)}^{\frac{3}{2}}}\end{array}$

The total magnetic field due to lower ring will be

   $\begin{array}{l}{H}_2={\displaystyle \underset{0}{\overset{2\pi }{\int }}\frac{Iad\varphi \left(a{a}_z\right)}{4\pi {\left(a^2+{\left(z+h\right)}^2\right)}^{\frac{3}{2}}}}\\ H_2=\frac{Ia\left(a{a}_z\right)}{4\pi {\left(a^2+{\left(z+h\right)}^2\right)}^{\frac{3}{2}}}{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\varphi }\\ H_2=\frac{Ia\left(a{a}_z\right)}{4\pi {\left(a^2+{\left(z+h\right)}^2\right)}^{\frac{3}{2}}}\left[2\pi \right]\\ H_2=\frac{I{a}^2}{2{\left(a^2+{\left(z+h\right)}^2\right)}^{\frac{3}{2}}}{a}_z\end{array}$

As the magnetic fields are linear, therefore, the magnetic field at point P will be the sum of both.

That is,

   $\begin{array}{l}{H}_{Total}=H_1+H_2\\ H_{Total}=\frac{I{a}^2{a}_z}{2{\left(a^2+{\left(z-h\right)}^2\right)}^{\frac{3}{2}}}+\frac{I{a}^2}{2{\left(a^2+{\left(z+h\right)}^2\right)}^{\frac{3}{2}}}{a}_z\\ H_{Total}=\frac{I{a}^2}{2}\left(\frac{1}{{\left(a^2+{\left(z-h\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(a^2+{\left(z+h\right)}^2\right)}^{\frac{3}{2}}}\right)a_z\\ \text{As,}I=1\text{A}\\ H_{Total}=\frac{a^2}{2}\left(\frac{1}{{\left(a^2+{\left(z-h\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(a^2+{\left(z+h\right)}^2\right)}^{\frac{3}{2}}}\right)a_z\end{array}$

The above expression is the value of magnetic field on the positive side of the z axis.

The total magnetic field an any point on the z axis between the range $-h<z<h$ will be

   $H_{Total}=\frac{I{a}^2}{2}\left(\frac{1}{{\left(a^2+{\left(z-h\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(a^2+{\left(z+h\right)}^2\right)}^{\frac{3}{2}}}\right)a_z$

To determine

(b)

To plot:

The graph of $\left|H\right|$ for $h=\frac{a}{4}$.

Explanation of Solution

Given:

The given configuration is

I = $1\text{A}$

   $h=\frac{a}{4}$

Calculation:

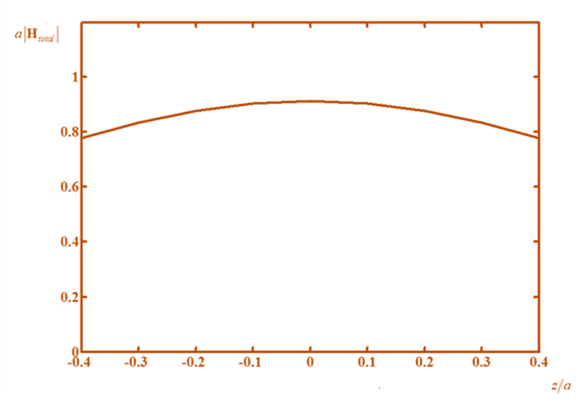
Substituting I = 1A and manipulating the equation for z/a, the modulus of total field will be

   $\left|H_{Total}\right|=\frac{a^2}{2}\left(\frac{1}{{\left(a^2+{\left(z-h\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(a^2+{\left(z+h\right)}^2\right)}^{\frac{3}{2}}}\right)$

   $\left|H_{Total}\right|=\frac{a^2}{2}\left(\frac{1}{{\left(a^2\right)}^{\frac{3}{2}}{\left(1+{\left(\frac{z-h}{a}\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(a^2\right)}^{\frac{3}{2}}{\left(1+{\left(\frac{z+h}{a}\right)}^2\right)}^{\frac{3}{2}}}\right)$

   $\left|H_{Total}\right|=\frac{1}{2a}\left(\frac{1}{{\left(1+{\left(z^{\prime }-h^{\prime }\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(1+{\left(z^{\prime }+h^{\prime }\right)}^2\right)}^{\frac{3}{2}}}\right)$

   $a\left|H_{Total}\right|=\frac{1}{2}\left(\frac{1}{{\left(1+{\left(z^{\prime }-h^{\prime }\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(1+{\left(z^{\prime }+h^{\prime }\right)}^2\right)}^{\frac{3}{2}}}\right)\mathrm{.............}\left(1\right)$

Put $h=\frac{a}{4}$ in equation 1,

   $\begin{array}{l}\left|H_{Total}\right|=\frac{1}{2a}\left(\frac{1}{{\left(1+{\left(z^{\prime }-\frac{\frac{a}{4}}{a}\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(1+{\left(z^{\prime }+\frac{\frac{a}{4}}{a}\right)}^2\right)}^{\frac{3}{2}}}\right)\\ \left|H_{Total}\right|=\frac{1}{2a}\left(\frac{1}{{\left(1+{\left(z^{\prime }-\frac{1}{4}\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(1+{\left(z^{\prime }+\frac{1}{4}\right)}^2\right)}^{\frac{3}{2}}}\right)\\ a\left|H_{Total}\right|=\frac{1}{2}\left(\frac{1}{{\left(1+{\left(z^{\prime }-\frac{1}{4}\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(1+{\left(z^{\prime }+\frac{1}{4}\right)}^2\right)}^{\frac{3}{2}}}\right)\end{array}$

Therefore, the plot will be

To determine

(c)

To plot:

The graph of $\left|H\right|$ for $h=\frac{a}{2}$.

Explanation of Solution

Given:

The given configuration is

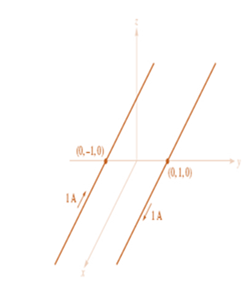
I = $1\text{A}$

   $h=\frac{a}{2}$

Calculation:

Substituting I = 1A and manipulating the equation for z / a, the modulus of total field will be

   $\left|H_{Total}\right|=\frac{a^2}{2}\left(\frac{1}{{\left(a^2+{\left(z-h\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(a^2+{\left(z+h\right)}^2\right)}^{\frac{3}{2}}}\right)$

   $\left|H_{Total}\right|=\frac{a^2}{2}\left(\frac{1}{{\left(a^2\right)}^{\frac{3}{2}}{\left(1+{\left(\frac{z-h}{a}\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(a^2\right)}^{\frac{3}{2}}{\left(1+{\left(\frac{z+h}{a}\right)}^2\right)}^{\frac{3}{2}}}\right)$

   $\left|H_{Total}\right|=\frac{1}{2a}\left(\frac{1}{{\left(1+{\left(z^{\prime }-h^{\prime }\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(1+{\left(z^{\prime }+h^{\prime }\right)}^2\right)}^{\frac{3}{2}}}\right)$

   $a\left|H_{Total}\right|=\frac{1}{2}\left(\frac{1}{{\left(1+{\left(z^{\prime }-h^{\prime }\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(1+{\left(z^{\prime }+h^{\prime }\right)}^2\right)}^{\frac{3}{2}}}\right)\mathrm{.............}\left(1\right)$

Put $h=\frac{a}{2}$ in equation 1,

   $\begin{array}{l}\left|H_{Total}\right|=\frac{1}{2a}\left(\frac{1}{{\left(1+{\left(z^{\prime }-\frac{\frac{a}{2}}{a}\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(1+{\left(z^{\prime }+\frac{\frac{a}{2}}{a}\right)}^2\right)}^{\frac{3}{2}}}\right)\\ \left|H_{Total}\right|=\frac{1}{2a}\left(\frac{1}{{\left(1+{\left(z^{\prime }-\frac{1}{2}\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(1+{\left(z^{\prime }+\frac{1}{2}\right)}^2\right)}^{\frac{3}{2}}}\right)\\ a\left|H_{Total}\right|=\frac{1}{2}\left(\frac{1}{{\left(1+{\left(z^{\prime }-\frac{1}{2}\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(1+{\left(z^{\prime }+\frac{1}{2}\right)}^2\right)}^{\frac{3}{2}}}\right)\end{array}$

Therefore, the plot will look li

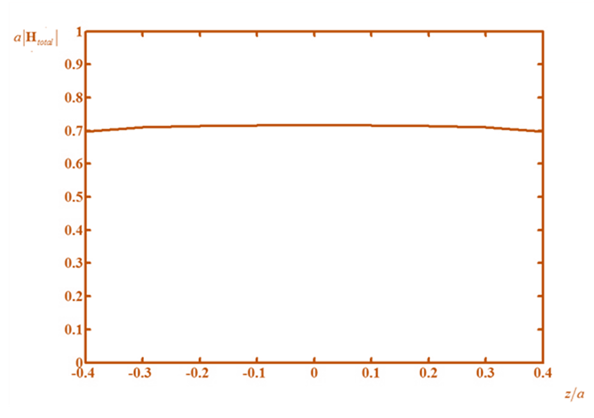
The most uniform field is obtained when $h=\frac{a}{2}$.

To determine

(d)

To plot:

The graph of $\left|H\right|$ for $h=a$ . Also, state the value of 'h' which will give the most uniform field as observed from part (b), (c) and (d).

Answer to Problem 7.4P

The most uniform field is obtained when $h=\frac{a}{2}$.

Explanation of Solution

Given:

The given configuration is

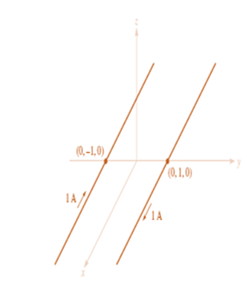
I = $1\text{A}$

   $h=a$

Calculation:

Substituting I = 1A and manipulating the equation for z/a, the modulus of total field will be

   $\left|H_{Total}\right|=\frac{a^2}{2}\left(\frac{1}{{\left(a^2+{\left(z-h\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(a^2+{\left(z+h\right)}^2\right)}^{\frac{3}{2}}}\right)$

   $\left|H_{Total}\right|=\frac{a^2}{2}\left(\frac{1}{{\left(a^2\right)}^{\frac{3}{2}}{\left(1+{\left(\frac{z-h}{a}\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(a^2\right)}^{\frac{3}{2}}{\left(1+{\left(\frac{z+h}{a}\right)}^2\right)}^{\frac{3}{2}}}\right)$

   $\left|H_{Total}\right|=\frac{1}{2a}\left(\frac{1}{{\left(1+{\left(z^{\prime }-h^{\prime }\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(1+{\left(z^{\prime }+h^{\prime }\right)}^2\right)}^{\frac{3}{2}}}\right)$

   $a\left|H_{Total}\right|=\frac{1}{2}\left(\frac{1}{{\left(1+{\left(z^{\prime }-h^{\prime }\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(1+{\left(z^{\prime }+h^{\prime }\right)}^2\right)}^{\frac{3}{2}}}\right)\mathrm{.............}\left(1\right)$

Put $h=a$ in equation 1,

   $\begin{array}{l}\left|H_{Total}\right|=\frac{1}{2a}\left(\frac{1}{{\left(1+{\left(z^{\prime }-1\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(1+{\left(z^{\prime }+1\right)}^2\right)}^{\frac{3}{2}}}\right)\\ \left|H_{Total}\right|=\frac{1}{2a}\left(\frac{1}{{\left(1+{\left(z^{\prime }-1\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(1+{\left(z^{\prime }+1\right)}^2\right)}^{\frac{3}{2}}}\right)\\ a\left|H_{Total}\right|=\frac{1}{2}\left(\frac{1}{{\left(1+{\left(z^{\prime }-1\right)}^2\right)}^{\frac{3}{2}}}+\frac{1}{{\left(1+{\left(z^{\prime }+1\right)}^2\right)}^{\frac{3}{2}}}\right)\end{array}$

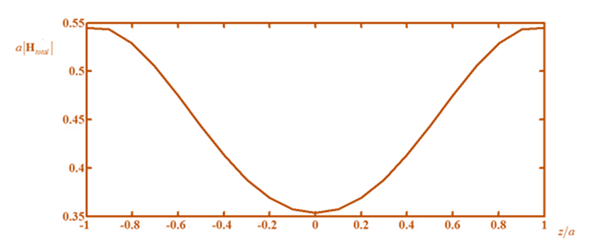
Therefore, the plot will look like