
The state of plane stress shown occurs in a machine component made of a steel with σy = 30 ksi. Using the maximum- distortion-energy criterion, determine whether yield will occur when (a) τXV = 6 ksi, (b) τXV = 12 ksi, (c) τXV = 14 ksi. If yield does not occur, determine the corresponding factor of safety.
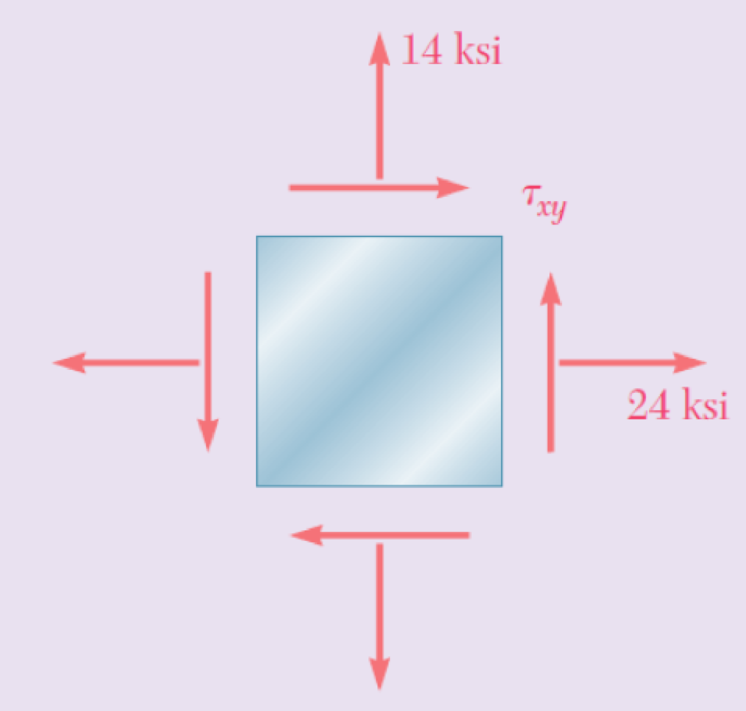
Fig. P7.164
(a)
Check the yield will occur for the given condition or not?.
Find the corresponding factor of safety for not occurring the yield.
Answer to Problem 164RP
The yielding will
Explanation of Solution
Given information:
The normal stress in x-axis is
The normal stress in y-axis is
The shearing stress in xy-plane is
The allowable yield strength of the steel is
Use maximum distortion-energy theory.
Calculation:
Consider the normal stress in z-axis is
The minimum principal stress is
Find the average normal stress
Substitute 24 ksi for
Find the radius of the Mohr circle (R) using the equation.
Substitute 24 ksi for
Find the maximum principal stress
Substitute 19 ksi for
Find the minimum principal stress
Substitute 19 ksi for
Check the yielding condition using the Maximum-distortion-energy criteria as follows;
Substitute 26.81 ksi for
The yielding will not occur.
Find the factor of safety (FOS) using the relation.
Substitute 30 ksi for
Therefore, the yielding will
(b)
Check the yield will occur for the given condition or not?.
Find the corresponding factor of safety for not occurring the yield.
Answer to Problem 164RP
The yielding will
Explanation of Solution
Given information:
The normal stress in x-axis is
The normal stress in y-axis is
The shearing stress in xy-plane is
The allowable yield strength of the steel is
Use maximum distortion-energy theory.
Calculation:
Consider the normal stress in z-axis is
The minimum principal stress is
Find the average normal stress
Substitute 24 ksi for
Find the radius of the Mohr circle (R) using the equation.
Substitute 24 ksi for
Find the maximum principal stress
Substitute 19 ksi for
Find the minimum principal stress
Substitute 19 ksi for
Check the yielding condition using the Maximum-distortion-energy criteria as follows;
Substitute 32 ksi for
The yielding will not occur.
Find the factor of safety (FOS) using the relation.
Substitute 30 ksi for
Therefore, the yielding will
(c)
Check the yield will occur for the given condition or not?.
Find the corresponding factor of safety for not occurring the yield.
Answer to Problem 164RP
The yielding will occur.
Explanation of Solution
Given information:
The normal stress in x-axis is
The normal stress in y-axis is
The shearing stress in xy-plane is
The allowable yield strength of the steel is
Use maximum distortion-energy theory.
Calculation:
Consider the normal stress in z-axis is
The minimum principal stress is
Find the average normal stress
Substitute 24 ksi for
Find the radius of the Mohr circle (R) using the equation.
Substitute 24 ksi for
Find the maximum principal stress
Substitute 19 ksi for
Find the minimum principal stress
Substitute 19 ksi for
Check the yielding condition using the Maximum-distortion-energy criteria as follows;
Substitute 33.866 ksi for
The yielding will occur.
Therefore, the yielding will occur.
Want to see more full solutions like this?
Chapter 7 Solutions
EBK MECHANICS OF MATERIALS
- Note: Please provide a clear, step-by-step simplified handwritten working out (no explanations!), ensuring it is done without any AI involvement. I require an expert-level answer, and I will assess and rate based on the quality and accuracy of your work and refer to the provided image for more clarity. Make sure to double-check everything for correctness before submitting appreciate your time and effort!. Question: If the flow rate through the system below is 0.04m3s-1, find the difference in elevation H of the two reservoirs.arrow_forwardNote: Please provide a clear, step-by-step simplified handwritten working out (no explanations!), ensuring it is done without any AI involvement. I require an expert-level answer, and I will assess and rate based on the quality and accuracy of your work and refer to the provided image for more clarity. Make sure to double-check everything for correctness before submitting thanks!. Question: (In the image as provided)arrow_forwardNote: Please provide a clear, step-by-step simplified handwritten working out (no explanations!), ensuring it is done without any AI involvement. I require an expert-level answer, and I will assess and rate based on the quality and accuracy of your work and refer to the provided image for more clarity. Make sure to double-check everything for correctness before submitting thanks!. Question: The rectangular gate shown below is 3 m wide. Compute the force P needed to hold the gate in the position shown.arrow_forward
- Note: Please provide a clear, step-by-step simplified handwritten working out (no explanations!), ensuring it is done without any AI involvement. I require an expert-level answer, and I will assess and rate based on the quality and accuracy of your work and refer to the provided image for more clarity. Make sure to double-check everything for correctness before submitting thanks!. Question1: If the following container is 0.6m high, 1.2m wide and half full with water, determine the pressure acting at points A, B, and C if ax=2.6ms^-2.arrow_forwardPlease read the imagearrow_forwardChapter 12 - Lecture Notes.pptx: (MAE 272-01) (SP25) DY... Scoresarrow_forwardConsider a large 6-cm-thick stainless steel plate (k = 15.1 W/m-K) in which heat is generated uniformly at a rate of 5 × 105 W/m³. Both sides of the plate are exposed to an environment at 30°C with a heat transfer coefficient of 60 W/m²K. Determine the value of the highest and lowest temperature. The highest temperature is The lowest temperature is °C. °C.arrow_forwardSketch and explain a PV Diagram and a Temperature Entropy Diagram for a 4 stroke diesel engine please, please explain into detail the difference bewteen the two and referance the a diagram. Please include a sketch or an image of each diagramarrow_forwardDraw left view of the first orthographic projectionarrow_forwardSketch and Describe a timing diagram for a 2 stroke diesel engine emphasis on the 2 stroke as my last answer explained 4 stroke please include a diagram or sketch.arrow_forwardA 4 ft 200 Ib 1000 Ib.ft C 2 ft 350 Ib - за в 2.5 ft 150 Ib 250 Ib 375 300 Ib Replace the force system acting on the frame. shown in the figure by a resultant force (magnitude and direction), and specify where its line of action intersects member (AB), measured from point (A).arrow_forwardA continuous flow calorimeter was used to obtain the calorific value of a sample of fuel and the following data collected: Mass of fuel: 2.25 kgInlet water temperature: 11 ° COutlet water temperature 60 ° CQuantity of water: 360 Liters Calorimeter efficiency: 85%Calculate the calorific value of the sample ( kJ / kg ). ive submitted this question twice and have gotten two way different answers. looking for some help thanksarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





