Chapter 6.P2, Problem 1P

Derive the system of equations (1) by applying Newton’s second law, $ma=F$, to each of the masses. Assume that the springs follow Hooke’s law: the force exerted by a spring on a mass is proportional to the length of its departure from its equilibrium length.

$m\frac{d^2{x}_1}{d{t}^2}=-2k{x}_1+k{x}_2+\widehat{u_1}\left(t\right),$

$m\frac{d^2{x}_2}{d{t}^2}=k{x}_1-2k{x}_2+k{x}_3+\widehat{u_2}\left(t\right),$ (1)

$m\frac{d^2{x}_3}{d{t}^2}=k{x}_2-2k{x}_3+\widehat{u_3}\left(t\right).$

To determine

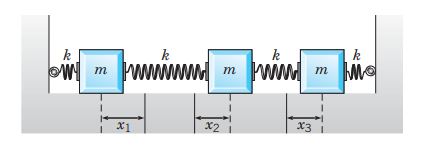
The system of equations describing motions of a three mass and four spring system by applying Newton’s second law $F=ma$ where $x_j\left(t\right),j=1,2,\mathrm{3..}$ represents the displacement of the masses $m$ from equilibrium positions at time $t$ and ${\widehat{u}}_j\left(t\right),j=1,2,\mathrm{3..}$ represents the external forces acting on the mass and assuming that springs follow Hooke’s Law.

Answer to Problem 1P

Solution:

The system of equations describing motions of a three mass and four spring system are $m\frac{d^2{x}_1}{d{t}^2}=-2k{x}_1+k{x}_2+{\widehat{u}}_1(t)$, $m\frac{d^2{x}_2}{d{t}^2}=k{x}_1-2k{x}_2+k{x}_3+{\widehat{u}}_2\left(t\right)$ and, $m\frac{d^2{x}_3}{d{t}^2}=k{x}_2-2k{x}_3+{\widehat{u}}_3\left(t\right)$.

Explanation of Solution

Given information:

Three masses $m$ are placed between two walls and attached to the wall and with each other by four springs of spring constant $k$.

$x_j\left(t\right),j=1,2,\mathrm{3..}$ represents the displacement of the masses $m$ from equilibrium positions at time $t$

${\widehat{u}}_j\left(t\right),j=1,2,\mathrm{3..}$ represents the external forces acting on the mass.

Newton’s second law is $F=ma$.

The springs follow Hooke’s Law: The force exerted by a spring on a mass is directly proportional to the length of its departure from its equilibrium length.

Explanation:

The first mass’s one side is attached to the wall with the spring and the other side is attached to the second body with another spring of spring constant $k$ and its displacement is $x_1\left(t\right)$ from its equilibrium position.

Then the velocity of the mass is $\frac{changeindisplacement}{changeintime}=\frac{d{x}_1}{dt}$

Then the acceleration of the mass is $\frac{changeinvelocity}{changeintime}=\frac{d}{dt}\left(\frac{d{x}_1}{dt}\right)=\frac{d^2{x}_1}{d{t}^2}$

By Newton’s law, the forces acting on the mass is $F=ma=m\frac{d^2{x}_1}{d{t}^2}$

By Hooke’s law, the forces acting on the mass is $-k{x}_1$ on the wall side and $k\left(x_2-x_1\right)$ on the other side.

Also, a force ${\widehat{u}}_1\left(t\right)$ is acting on the body externally.

Then the equation of motion of the first body is $m\frac{d^2{x}_1}{d{t}^2}=-k{x}_1+k\left(x_2-x_1\right)+{\widehat{u}}_1\left(t\right)$

$\Rightarrow m\frac{d^2{x}_1}{d{t}^2}=-2k{x}_1+k{x}_2+{\widehat{u}}_1(t)$

In the second case, the second body is attached to the first body with the spring and the other side is attached to the third body with another spring of spring constant $k$ and its displacement is $x_2\left(t\right)$ from its equilibrium position.

Then the velocity of the mass is $\frac{changeindisplacement}{changeintime}=\frac{d{x}_2}{dt}$

Then the acceleration of the mass is $\frac{changeinvelocity}{changeintime}=\frac{d}{dt}\left(\frac{d{x}_1}{dt}\right)=\frac{d^2{x}_2}{d{t}^2}$

By Newton’s law, the forces acting on the mass is $F=ma=m\frac{d^2{x}_2}{d{t}^2}$

By Hooke’s law, the forces acting on the mass is $-k\left(x_2-x_1\right)$ on the first body side and $k\left(x_3-x_2\right)$ on the other side.

Also, a force ${\widehat{u}}_2\left(t\right)$ is acting on the body externally.

Then the equation of motion of the second body is $m\frac{d^2{x}_2}{d{t}^2}=-k\left(x_2-x_1\right)+k\left(x_3-x_2\right)+{\widehat{u}}_2\left(t\right)$

$\Rightarrow m\frac{d^2{x}_2}{d{t}^2}=-k{x}_2+k{x}_1+k{x}_3-k{x}_2+{\widehat{u}}_2(t)$

$\Rightarrow m\frac{d^2{x}_2}{d{t}^2}=-2k{x}_2+k{x}_1+k{x}_3+{\widehat{u}}_2(t)$

Similarly, in the third case, the third mass is attached to the wall with the spring and in the other side, it is attached to the second body with another spring of spring constant $k$ and its displacement is $x_3\left(t\right)$ from its equilibrium position.

Then the velocity of the mass is $\frac{changeindisplacement}{changeintime}=\frac{d{x}_3}{dt}$

Then the acceleration of the mass is $\frac{changeinvelocity}{changeintime}=\frac{d}{dt}\left(\frac{d{x}_3}{dt}\right)=\frac{d^2{x}_3}{d{t}^2}$

By Newton’s law, the forces acting on the mass is $F=ma=m\frac{d^2{x}_3}{d{t}^2}$

By Hooke’s law, the forces acting on the mass is $-k\left(x_3-x_2\right)$ on the wall side and $-k{x}_3$ on the other side.

Also, a force ${\widehat{u}}_3\left(t\right)$ is acting on the body externally.

Then the equation of motion of the third body is $m\frac{d^2{x}_3}{d{t}^2}=-k{x}_3-k\left(x_3-x_2\right)+{\widehat{u}}_3\left(t\right)$

$\Rightarrow m\frac{d^2{x}_3}{d{t}^2}=-2k{x}_3+k{x}_2+{\widehat{u}}_3\left(t\right)$

Thus, the system of equations describing the motions of a three mass and four spring system are $m\frac{d^2{x}_1}{d{t}^2}=-2k{x}_1+k{x}_2+{\widehat{u}}_1(t)$, $m\frac{d^2{x}_2}{d{t}^2}=k{x}_1-2k{x}_2+k{x}_3+{\widehat{u}}_2\left(t\right)$, $m\frac{d^2{x}_3}{d{t}^2}=k{x}_2-2k{x}_3+{\widehat{u}}_3\left(t\right)$.