
Diffusion on a One-dimensional Lattice with an Absorbing Boundary. Consider a one-dimensional lattice consisting of
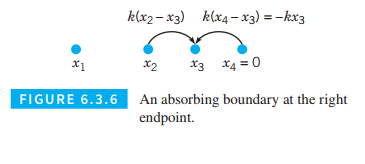
Assume that the left endpoint is a reflecting boundary so that the rate equation for the number of particles
(a) Find the system of differential equations that describe the rate equation for
(b) Site
and explain the meaning of this equation.
(c) Find the eigenvalues and eigenvectors for the matrix
(d) Find the general solution of the system of equations found in part (a).Explain the asymptotic behavior of
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
DIFFERENTIAL EQUATIONS-NEXTGEN WILEYPLUS
Additional Math Textbook Solutions
Pre-Algebra Student Edition
Calculus: Early Transcendentals (2nd Edition)
Introductory Statistics
University Calculus: Early Transcendentals (4th Edition)
Thinking Mathematically (6th Edition)
STATISTICS F/BUSINESS+ECONOMICS-TEXT
- 30.1. Show that z = 0 is a removable singularity of the following functions. Furthermore, define f(0) such that these functions are analytic at z = 0. (a). f(z) = 2 sin z- z 1-12² - cos z (b). f(z) = (c). f(z) = sin 22arrow_forward3. Consider the polynomial equation 6-iz+7z² -iz³ +z = 0 for which the roots are 3i, -2i, -i, and i. (a) Verify the relations between this roots and the coefficients of the polynomial. (b) Find the annulus region in which the roots lie.arrow_forward30.3. Find and classify the isolated singularities of the following func- tions: (a). 23+1 22(2-1) (b). ²e¹/, (c). sin 3z (d). COS 2arrow_forward
- 3. Consider the polynomial equation 6-iz+7z2-iz³ +z = 0 for which the roots are 3i, -2i, -i, and i. (a) Verify the relations between this roots and the coefficients of the polynomial. (b) Find the annulus region in which the roots lie.arrow_forwardDetermine the set of odd primes p for which 23 is a quadratic residue.arrow_forwardPatterns in Floor Tiling A square floor is to be tiled with square tiles as shown. There are blue tiles on the main diagonals and red tiles everywhere else. In all cases, both blue and red tiles must be used. and the two diagonals must have a common blue tile at the center of the floor. If 81 blue tiles will be used, how many red tiles will be needed? For what numbers in place of 81 would this problem still be solvable? Find an expression in k giving the number of red tiles required in general.arrow_forward
- Solve questionsarrow_forwardQ/ Find and classify the singularities of the functions- = 52+3 (1-2) sin² Z a fcz) b f(z) = tanz Z © f(2)= [z (e²-1)]arrow_forwardThe managing director of a consulting group has the accompanying monthly data on total overhead costs and professional labor hours to bill to clients. Complete parts a through c Overhead Costs Billable Hours345000 3000385000 4000410000 5000462000 6000530000 7000545000 8000arrow_forward
- Using the accompanying Home Market Value data and associated regression line, Market ValueMarket Valueequals=$28,416plus+$37.066×Square Feet, compute the errors associated with each observation using the formula e Subscript ieiequals=Upper Y Subscript iYiminus−ModifyingAbove Upper Y with caret Subscript iYi and construct a frequency distribution and histogram. Square Feet Market Value1813 911001916 1043001842 934001814 909001836 1020002030 1085001731 877001852 960001793 893001665 884001852 1009001619 967001690 876002370 1139002373 1131001666 875002122 1161001619 946001729 863001667 871001522 833001484 798001589 814001600 871001484 825001483 787001522 877001703 942001485 820001468 881001519 882001518 885001483 765001522 844001668 909001587 810001782 912001483 812001519 1007001522 872001684 966001581 86200arrow_forwardPatterns in Floor Tiling A square floor is to be tiled with square tiles as shown. There are blue tiles on the main diagonals and red tiles everywhere else. In all cases, both blue and red tiles must be used. and the two diagonals must have a common blue tile at the center of the floor. If 81 blue tiles will be used, how many red tiles will be needed?arrow_forwardAt a BBQ, you can choose to eat a burger, hotdog or pizza. you can choose to drink water, juice or pop. If you choose your meal at random, what is the probability that you will choose juice and a hot dog? What is the probability that you will not choose a burger and choose either water or pop?arrow_forward
 Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
 Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning, Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education





