Chapter 6.4, Problem 56E

(a)

To determine

To prove : The statement is $\underset{x\to \infty }{\lim }{\left(1+\frac{1}{x}\right)}^x=e$

Explanation of Solution

Given information:

The statement is $\underset{x\to \infty }{\lim }{\left(1+\frac{1}{x}\right)}^x=e$

Calculation:

  $e\approx 2.718$

And the table is:

$x$	$y$
1	2
10	2.5937
100	2.7048
1000	2.7169
10000	2.7181
100000	2.7183

The graph is shown below:

  

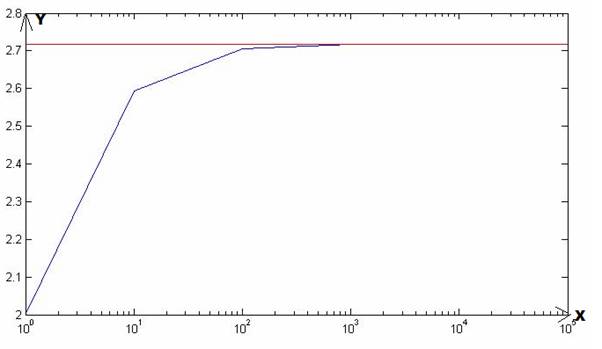
Therefore, the required given statement $\underset{x\to \infty }{\lim }{\left(1+\frac{1}{x}\right)}^x=e$ is $($ proved $)$ .

(b)

To determine

To prove: The given statement.

Explanation of Solution

Given information:

The statement is $\underset{x\to \infty }{\lim }{\left(1+\frac{r}{x}\right)}^x=e^r$

Calculation:

If $r=2$

Then ,

  $\begin{array}{c}\underset{x\to \infty }{\lim }{\left(1+\frac{2}{x}\right)}^x=e^2\\ \approx \mathrm{7.3891.}\end{array}$

Input,

  $Y_1={\left(1+\frac{2}{x}\right)}^x$ into the calculator then use the table to find values for large values for $\text{x}$ to verify numerically that the limit is ${\text{e}}^2$ .

$\text{x}$	${\text{Y}}_1$
10	6.1917
100	7.2446
1,000	7.3743
10,000	7.3876
100,000	7.389
${\text{10}}^6$	7.3891
${\text{10}}^7$	7.3891

The graph is shown below:

  

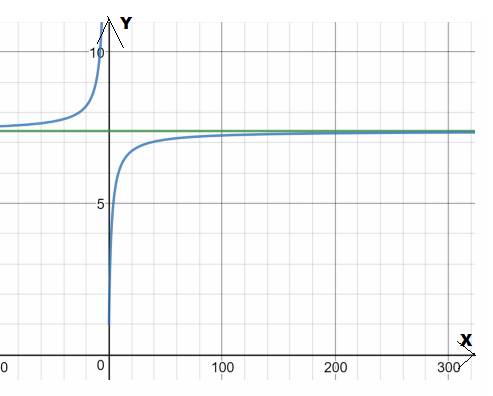
If $r=3$ ,

Then ,

  $\begin{array}{c}\underset{x\to \infty }{\lim }{\left(1+\frac{3}{x}\right)}^x=e^3\\ \approx 20.086\end{array}$

Input $Y_1={\left(1+\frac{3}{x}\right)}^x$

  $Y_1={\left(1+\frac{2}{x}\right)}^x$ into the calculator then use the table to find values for large values for $\text{x}$ to verify numerically that the limit is ${\text{e}}^3$ .

$\text{x}$	${\text{Y}}_1$
10	13.786
100	19.219
1,000	19.996
10,000	20.077
100,000	20.085
${\text{10}}^6$	20.086
${\text{10}}^7$	20.086

The graph is shown below:

  

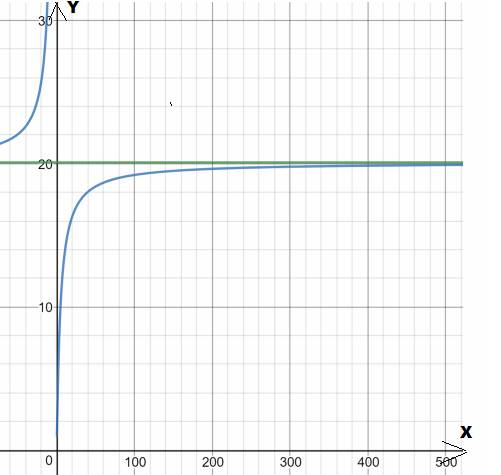
Therefore, , the required given statement $\underset{x\to \infty }{\lim }{\left(1+\frac{r}{x}\right)}^x=e^r$ is $($ proved $)$ .

(c)

To determine

To explain: The given statement.

Answer to Problem 56E

  $n$ gets larger and larger, then,

  $\begin{array}{c}A=P{\left[{\left(1+\frac{r}{n}\right)}^n\right]}^t\\ \to P{\left(e^r\right)}^t=P{e}^{rt}\end{array}$

which is the formula for interest compounded continuously.

Explanation of Solution

Given information:

The idea of interest compounded continuously results from the compounding of interest over ever-shorter time periods.

Calculation:

The compound interest value is $A=P{\left(1+\frac{r}{n}\right)}^{nt}$ .

Compounding interest over smaller and smaller periods means nn gets larger and larger. From part $(b)$ , $\underset{n\to \infty }{\lim }{\left(1+\frac{r}{n}\right)}^n=e^r$ .

So, $n$ gets larger and larger, then,

  $\begin{array}{c}A=P{\left[{\left(1+\frac{r}{n}\right)}^n\right]}^t\\ \to P{\left(e^r\right)}^t=P{e}^{rt}\end{array}$

which is the formula for interest compounded continuously.