Chapter 6.1, Problem 6.35P

To determine

The force in each of the members of the truss for the given loading.

Answer to Problem 6.35P

The force in member AC is $1040\text{ lb}$ and the member AC is in tension, the force in members $BC\text{ and }CD$ is $500\text{ lb}$ and these members are in compression, the force in members $AB\text{ and }AD$ is $244\text{ lb}$ and these members are in compression, the force in member $BD$ is $280\text{ lb}$ and it is in tension.

Explanation of Solution

The free-body diagram of the entire truss is shown in figure 1.

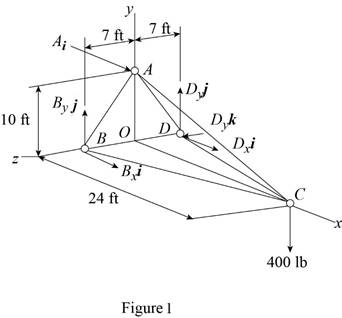
Refer to figure 1 and use symmetry.

$\begin{array}{c}{D}_x=B_x\\ D_y=B_y\end{array}$ (I)

Here, $D_x$ is the $x$ component of the reaction at the point D, $D_y$ is the $y$ component of the reaction at the point D, $B_x$ is the $x$ component of the reaction at the point B and $B_y$ is the $y$ component of the reaction at the point B.

Write the equilibrium equations taking the moments about $z$ axis.

$\Sigma M_z=0$ (II)

Here, $\Sigma M_z$ is the sum of the moments about $z$ axis.

Write the equation for $\Sigma M_z$ .

$\Sigma M_z=-A\left(10\text{ ft}\right)-\left(400\text{ lb}\right)\left(24\text{ ft}\right)$

Here, $A$ is the reaction at the point A.

Put the above equation in equation (II).

$\begin{array}{c}-A\left(10\text{ ft}\right)-\left(400\text{ lb}\right)\left(24\text{ ft}\right)=0\\ A=-960\text{ lb}\end{array}$

The $x$ component of the net force must be equal to zero.

$\Sigma {\overrightarrow{F}}_x=0$ (III)

Here, $\Sigma {\overrightarrow{F}}_x$ is the $x$ component of the net force.

Write the expression for $\Sigma {\overrightarrow{F}}_x$ .

$\Sigma {\overrightarrow{F}}_x=B_x+D_x+A$

Put the above equation in equation (III).

$B_x+D_x+A=0$

Put equation (I) in the above equation.

$\begin{array}{c}{B}_x+B_x+A=0\\ 2B_x+A=0\\ B_x=\frac{-A}{2}\end{array}$

Substitute $-960\text{ lb}$ for $A$ in the above equation to find $B_x$ .

$\begin{array}{c}{B}_x=\frac{-\left(-960\text{ lb}\right)}{2}\\ =480\text{ lb}\end{array}$

The $y$ component of the net force must be equal to zero.

$\Sigma {\overrightarrow{F}}_y=0$ (IV)

Here, $\Sigma {\overrightarrow{F}}_y$ is the $y$ component of the net force.

Write the expression for $\Sigma {\overrightarrow{F}}_y$ .

$\Sigma F_y=B_y+D_y-400\text{ lb}$

Put the above equation in equation (IV).

$B_y+D_y-400\text{ lb=0}$

Put equation (I) in the above equation.

$\begin{array}{c}{B}_y+B_y-400\text{ lb}=0\\ 2B_y-400\text{ lb}=0\\ B_y=200\text{ lb}\end{array}$

Write the expression for the reaction at the point B.

$\overrightarrow{B}=B_x\widehat{i}+B_y\widehat{j}$

Here $\overrightarrow{B}$ is the reaction at the point B.

Substitute $480\text{ lb}$ for $B_x$ and $200\text{ lb}$ for $B_y$ in the above equation to find $\overrightarrow{B}$ .

$\overrightarrow{B}=\left(480\text{ lb}\right)\widehat{i}+\left(200\text{ lb}\right)\widehat{j}$

Consider the free-body joint C. The free-body diagram of joint C is shown in figure 2.

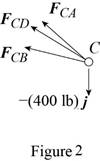
Refer to figure (2) and write the expression for the forces.

${\overrightarrow{F}}_{CA}=F_{AC}\frac{\overrightarrow{CA}}{CA}$ (V)

Here, ${\overrightarrow{F}}_{CA}$ is the force exerted by member CA and $CA$ is the magnitude of the vector $\overrightarrow{CA}$ .

Write the expression for $\overrightarrow{CA}$ .

$\overrightarrow{CA}=-24\widehat{i}+10\widehat{j}$

Find the magnitude of $\overrightarrow{CA}$ .

$\begin{array}{c}CA=\sqrt{{\left(-24\right)}^2+{10}^2}\\ =26\end{array}$

Substitute $-24\widehat{i}+10\widehat{j}$ for $\overrightarrow{CA}$ and $26$ for $CA$ in equation (V) to find the expression for ${\overrightarrow{F}}_{CA}$ .

${\overrightarrow{F}}_{CA}=F_{AC}\frac{\left(-24\widehat{i}+10\widehat{j}\right)}{26}$ (VI)

Write the expression for ${\overrightarrow{F}}_{CB}$ .

${\overrightarrow{F}}_{CB}=F_{BC}\frac{\overrightarrow{CB}}{CB}$

Here, ${\overrightarrow{F}}_{CB}$ is the force exerted by member CB and $CB$ is the magnitude of the vector $\overrightarrow{CB}$ .

Substitute $-24\widehat{i}+7\widehat{k}$ for $\overrightarrow{CB}$ and $25$ for $CB$ in the above equation to find the expression for ${\overrightarrow{F}}_{CB}$ .

${\overrightarrow{F}}_{CB}=F_{BC}\frac{\left(-24\widehat{i}+7\widehat{k}\right)}{25}$ (VII)

Write the expression for ${\overrightarrow{F}}_{CD}$ .

${\overrightarrow{F}}_{CD}=F_{CD}\frac{\overrightarrow{CD}}{CD}$

Here, ${\overrightarrow{F}}_{CD}$ is the force exerted by member CD and $CD$ is the magnitude of the vector $\overrightarrow{CD}$ .

Substitute $-24\widehat{i}-7\widehat{k}$ for $\overrightarrow{CD}$ and $25$ for $CD$ in the above equation to find the expression for ${\overrightarrow{F}}_{CD}$ .

${\overrightarrow{F}}_{CD}=F_{CD}\frac{\left(-24\widehat{i}-7\widehat{k}\right)}{25}$ (VIII)

The net force must be equal to zero.

$\Sigma \overrightarrow{F}=0$ (IX)

Here, $\Sigma \overrightarrow{F}$ is the net force.

Write the expression for $\Sigma \overrightarrow{F}$ .

$\Sigma \overrightarrow{F}={\overrightarrow{F}}_{CA}+{\overrightarrow{F}}_{CB}+{\overrightarrow{F}}_{CD}-\left(400\text{ lb}\right)\widehat{j}$

Put the above equation in equation (IX).

${\overrightarrow{F}}_{CA}+{\overrightarrow{F}}_{CB}+{\overrightarrow{F}}_{CD}-\left(400\text{ lb}\right)\widehat{j}=0$

Put equations (VI), (VII) and (VIII) in the above equation.

$F_{AC}\frac{\left(-24\widehat{i}+10\widehat{j}\right)}{26}+F_{BC}\frac{\left(-24\widehat{i}+7\widehat{k}\right)}{25}+F_{CD}\frac{\left(-24\widehat{i}-7\widehat{k}\right)}{25}-\left(400\text{ lb}\right)\widehat{j}=0$ (X)

Equate the coefficient of $\widehat{i}$ in equation (X) to zero.

$-\frac{24}{26}{F}_{AC}-\frac{24}{25}\left(F_{BC}+F_{CD}\right)=0$ (XI)

Equate the coefficient of $\widehat{j}$ in equation (X) to zero.

$\begin{array}{c}\frac{10}{26}{F}_{AC}-400\text{ lb}=0\\ F_{AC}=1040\text{ lb, tension}\end{array}$

Equate the coefficient of $\widehat{k}$ in equation (X) to zero.

$\begin{array}{c}\frac{7}{25}\left(F_{BC}-F_{CD}\right)=0\\ F_{CD}=F_{BC}\end{array}$ (XII)

Put the above equation in equation (XI).

$\begin{array}{c}-\frac{24}{26}{F}_{AC}-\frac{24}{25}\left(F_{BC}+F_{BC}\right)=0\\ -\frac{24}{26}{F}_{AC}-\frac{24}{25}\left(2F_{BC}\right)=0\end{array}$

Substitute $1040\text{ lb}$ for $F_{AC}$ in the above equation.

$\begin{array}{c}-\frac{24}{26}\left(1040\text{ lb}\right)-\frac{24}{25}\left(2F_{BC}\right)=0\\ F_{BC}=-500\text{ lb}\\ F_{BC}=500\text{ lb, compression}\end{array}$

Consider the free-body joint B. The free-body diagram of joint B is shown in figure 3.

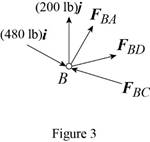
Refer to figure (3) and write the expression for the forces.

${\overrightarrow{F}}_{BC}=F_{BC}\frac{\overrightarrow{CB}}{CB}$ (XIII)

Here, ${\overrightarrow{F}}_{BC}$ is the force exerted by member BC

Substitute $500\text{ lb}$ for $F_{BC}$ , $-24\widehat{i}+7\widehat{k}$ for $\overrightarrow{CB}$ and $25$ for $CB$ in equation (XIII) to find the expression for ${\overrightarrow{F}}_{BC}$ .

$\begin{array}{c}{\overrightarrow{F}}_{BC}=\left(500\text{ lb}\right)\frac{\left(-24\widehat{i}+7\widehat{k}\right)}{25}\\ =-\left(480\text{ lb}\right)\widehat{i}+\left(140\text{ lb}\right)\widehat{k}\end{array}$ (XIV)

Write the expression for ${\overrightarrow{F}}_{BA}$ .

${\overrightarrow{F}}_{BA}=F_{AB}\frac{\overrightarrow{BA}}{BA}$

Here, ${\overrightarrow{F}}_{BA}$ is the force exerted by member BA and $BA$ is the magnitude of the vector $\overrightarrow{BA}$ .

Substitute $10\widehat{j}-7\widehat{k}$ for $\overrightarrow{BA}$ and $12.21$ for $BA$ in the above equation to find the expression for ${\overrightarrow{F}}_{BA}$ .

${\overrightarrow{F}}_{BA}=F_{AB}\frac{\left(10\widehat{j}-7\widehat{k}\right)}{12.21}$ (XV)

Write the expression for ${\overrightarrow{F}}_{BD}$ .

${\overrightarrow{F}}_{BD}=-F_{BD}\widehat{k}$ (XVI)

Here, ${\overrightarrow{F}}_{BD}$ is the force exerted by member BD

Write the expression for $\Sigma \overrightarrow{F}$ .

$\Sigma \overrightarrow{F}={\overrightarrow{F}}_{BA}+{\overrightarrow{F}}_{BD}+{\overrightarrow{F}}_{BC}+\overrightarrow{B}$

Put the above equation in equation (IX).

${\overrightarrow{F}}_{BA}+{\overrightarrow{F}}_{BD}+{\overrightarrow{F}}_{BC}+\overrightarrow{B}=0$

Put equations (XIV), (XV) and (XVI) in the above equation.

$-\left(480\text{ lb}\right)\widehat{i}+\left(140\text{ lb}\right)\widehat{k}+F_{AB}\frac{\left(10\widehat{j}-7\widehat{k}\right)}{12.21}-F_{BD}\widehat{k}+\overrightarrow{B}=0$

Substitute $\left(480\text{ lb}\right)\widehat{i}+\left(200\text{ lb}\right)\widehat{j}$ for $\overrightarrow{B}$ in the above equation.

$-\left(480\text{ lb}\right)\widehat{i}+\left(140\text{ lb}\right)\widehat{k}+F_{AB}\frac{\left(10\widehat{j}-7\widehat{k}\right)}{12.21}-F_{BD}\widehat{k}+\left(480\text{ lb}\right)\widehat{i}+\left(200\text{ lb}\right)\widehat{j}=0$ (XVII)

Equate the coefficient of $\widehat{j}$ in equation (XVII) to zero.

$\begin{array}{c}\frac{10}{12.21}{F}_{AB}+200\text{ lb}=0\\ F_{AB}=-244.2\text{ lb}\\ =244\text{ lb, compression}\end{array}$

Equate the coefficient of $\widehat{k}$ in equation (XVII) to zero.

$\begin{array}{c}-\frac{7}{12.21}{F}_{AB}-F_{BD}+140\text{ lb}=0\\ F_{BD}=-\frac{7}{12.21}{F}_{AB}+140\text{ lb}\end{array}$

Substitute $-244.2\text{ lb}$ for $F_{AB}$ in the above equation.

$\begin{array}{c}{F}_{BD}=-\frac{7}{12.21}\left(-244.2\text{ lb}\right)+140\text{ lb}\\ =280\text{ lb, tension}\end{array}$

From symmetry,

$F_{AD}=F_{AB}$

Here, $F_{AD}$ is the force exerted by AD.

Substitute $244\text{ lb, compression}$ for $F_{AB}$ in the above equation to find $F_{AD}$ .

$F_{AD}=244\text{ lb, compression}$

Conclusion:

Thus, the force in member AC is $1040\text{ lb}$ and the member AC is in tension, the force in members $BC\text{ and }CD$ is $500\text{ lb}$ and these members are in compression, the force in members $AB\text{ and }AD$ is $244\text{ lb}$ and these members are in compression, the force in member $BD$ is $280\text{ lb}$ and it is in tension.