
Concept explainers
School days: The following table presents the numbers of students enrolled in grades 1 through 8 in public schools in the United States.
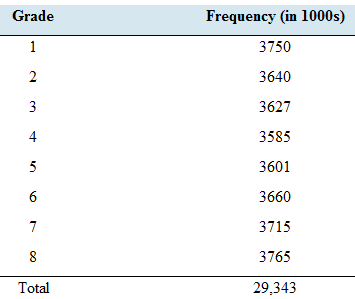
Consider these students to be a population. Let X be the grade of a student randomly chosen from this population.
Construct the
Find the probability that the student is in fourth grade.
Find the probability that the student is seventh or eighth grade.
Compute the
Compute the standard
a.
To construct: The probability distribution of the given random variable.
Explanation of Solution
The enrollment of students from grade
Calculation:
The random variable
To calculate the probability of each value of the random variable, the frequency should be divided by the total number of individuals according to the formula,
As an example,
The all calculation can be expressed in a table as follows. Because both values in the numerator and the denominator is in thousands, in the division those are cancelled out.
The probability distribution can be constructed by the first and third columns of the above table.
b.
To find: The probability to a selected student is from grade four.
Answer to Problem 49E
The probability that the student is in fourth grade is found to be
Explanation of Solution
The probability distribution for the grade of
Calculation:
When a student is fin grade four, the random variable
The relevant probability is calculated in a precious part as,
Conclusion:
The probability of
c.
To find: The probability to a selected student is in grade seven or eight.
Answer to Problem 49E
The probability that the student is seventh or eighth grade is found to be
Explanation of Solution
The probability distribution for the grade of
Calculation:
Same student cannot enroll to two different grades. Hence, being a grade seven student and being a grade eight student are two mutually exclusive events.
Therefore, the probability for this combination can be written as,
By the addition rule, this probability should be equal to
The total probability can be determined as,
Conclusion:
The probability of
d.
To find: The mean of grade of the student.
Answer to Problem 49E
The mean is found to be,
Explanation of Solution
The probability distribution for the grade of
Calculation:
The mean of a random variable, or equivalently the expected value is given by the sum of the product of the values and the corresponding probabilities.
Here, for each value of
Conclusion:
The mean is found to be
e.
To find: The standard deviation of
Answer to Problem 49E
The standard deviation is found to be,
Explanation of Solution
The probability distribution for the grade of
Calculation:
The variance of a random variable
By constructing a table we can do the calculations clearly using the mean of
The sum of right-most column gives the variation of
The standard deviation
Conclusion:
The standard deviation is found to be
Want to see more full solutions like this?
Chapter 6 Solutions
ELEMENTARY STATISTICS-ALEKS ACCESS CODE
- (c) Utilize Fubini's Theorem to demonstrate that E(X)= = (1- F(x))dx.arrow_forward(c) Describe the positive and negative parts of a random variable. How is the integral defined for a general random variable using these components?arrow_forward26. (a) Provide an example where X, X but E(X,) does not converge to E(X).arrow_forward
- (b) Demonstrate that if X and Y are independent, then it follows that E(XY) E(X)E(Y);arrow_forward(d) Under what conditions do we say that a random variable X is integrable, specifically when (i) X is a non-negative random variable and (ii) when X is a general random variable?arrow_forward29. State the Borel-Cantelli Lemmas without proof. What is the primary distinction between Lemma 1 and Lemma 2?arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
