
Concept explainers
Relax! The General Social Survey asked 1676 people how many hours per day they were able to relax. The results are presented in the following table.
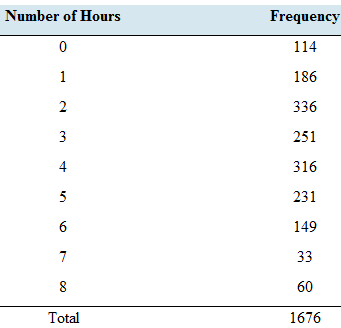
Consider these 1676 people to be a population. Let X be the number of hours of relaxation for a person sampled at random from this population.
Construct the
Find the probability that a person relaxes more than 4 hours per day.
Find the probability that a person doesn’t relax at all.
Compute the
Compute the standard deviation

a.
To construct:The probability distribution of the given random variable.
Explanation of Solution
The relaxing time of
Calculation:
The random variable
To calculate the probability of each value of the random variable, the frequency should be divided by the total number of individuals according to the formula,
As an example,
The all calculation can be expressed in a table as follows.
The probability distribution can be constructed by the first and third columns of the above table.
b.
To find:The probability to the relaxation time to be more than four hours.
Answer to Problem 47E
The probability to that a person relaxes more than four hours is
Explanation of Solution
The probability distribution for relaxing time of
Calculation:
Having relaxation for more than four hours means the random variable
The probability can be expressed in the notation as,
Since
Conclusion:
The probability of relaxation hours
c.
To find:The probability to the relaxation time is zero.
Answer to Problem 47E
The probability to that a person does not take any relax is found to be
Explanation of Solution
The probability distribution for relaxing time of
When a person does not relax at all, the relaxation time is equal to zero. Hence, the random variable should be
The relevant probability is calculated in a precious part as,
Conclusion:
The probability of
d.
To find: The mean relaxation time.
Answer to Problem 47E
The mean is found to be,
Explanation of Solution
The probability distribution for relaxing time of
The mean of a random variable, or equivalently the expected value is given by the sum of the product of the values and the corresponding probabilities.
Here, for each value of
Conclusion:
The mean number of relaxation time is found to be
e.
To find:The standard deviation of
Answer to Problem 47E
The standard deviation is found to be,
Explanation of Solution
The probability distribution for relaxing time of
The variance of a random variable
By constructing a table we can do the calculations clearly using the mean of
The sum of right-most column gives the variation of
The standard deviation
Conclusion:
The standard deviation is found to be
Want to see more full solutions like this?
Chapter 6 Solutions
ELEMENTARY STATISTICS-ALEKS ACCESS CODE
- (b) Demonstrate that if X and Y are independent, then it follows that E(XY) E(X)E(Y);arrow_forward(d) Under what conditions do we say that a random variable X is integrable, specifically when (i) X is a non-negative random variable and (ii) when X is a general random variable?arrow_forward29. State the Borel-Cantelli Lemmas without proof. What is the primary distinction between Lemma 1 and Lemma 2?arrow_forward
- The masses measured on a population of 100 animals were grouped in the following table, after being recorded to the nearest gram Mass 89 90-109 110-129 130-149 150-169 170-189 > 190 Frequency 3 7 34 43 10 2 1 You are given that the sample mean of the data is 131.5 and the sample standard deviation is 20.0. Test the hypothesis that the distribution of masses follows a normal distribution at the 5% significance level.arrow_forwardstate without proof the uniqueness theorm of probability functionarrow_forward(a+b) R2L 2+2*0=? Ma state without proof the uniqueness theorm of probability function suppose thatPandQ are probability measures defined on the same probability space (Q, F)and that Fis generated by a π-system if P(A)=Q(A) tax for all A EthenP=Q i. e. P(A)=Q(A) for alla g // معدلة 2:23 صarrow_forward
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill


