Chapter 6.1, Problem 19E

(a)

To determine

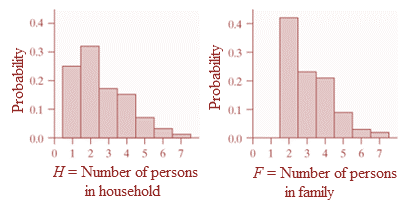
Differences, if any, while comparing the probability distributions of H and F using histogram.

Answer to Problem 19E

Both distributions are skewed to right with two persons and household having greater spread.

Neither distribution shows outliers.

Explanation of Solution

Given information:

H : the number of people in randomly selected U.S. household

F : the number of people in randomly selected U.S. family

Distributions of household size and family size in U.S:

  

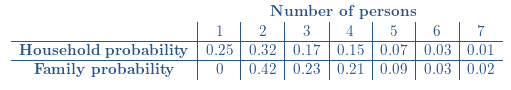
Histograms for F and H :

  

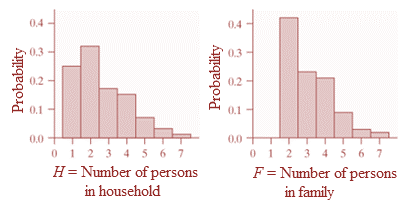
Shape: In the histograms, the highest bars are to the left, whereas a tail of smaller bars is to the right. Thus, both distributions are skewed to the right.

Center: Since the highest bar in both histograms is centered at 2, the most typical number of person in a family as well as in a household is 2.

Spread: Since the histogram of families is narrower than the histogram of households, the spread of number of persons in a household is greater than the spread of number of persons in a family.

Unusual features: Since there are no gaps in the histogram, neither distribution shows outliers.

(b)

To determine

Expected value of each random variable and relevance for this difference.

Answer to Problem 19E

Expected values (mean),

For H :

  ${\mu }_H=2.6$

For F :

  ${\mu }_F=3.14$

Explanation of Solution

Given information:

H : the number of people in randomly selected U.S. household

F : the number of people in randomly selected U.S. family

Distributions of household size and family size in U.S:

  

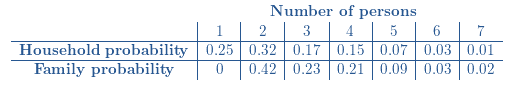
Histograms for F and H :

  

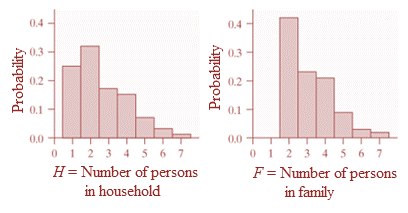
The expected mean is the sum of the product of each possibility x with its probability $P\left(X=x\right)$ .

For Household:

  $\begin{array}{l}{\mu }_H={\displaystyle \sum xP\left(X=x\right)}\\ =1\times 0.25+2\times 0.32+3\times 0.17\\ +4\times 0.15+5\times 0.07+6\times 0.03\\ +7\times 0.01\\ =2.6\end{array}$

For Family:

  $\begin{array}{l}{\mu }_F={\displaystyle \sum xP\left(X=x\right)}\\ =1\times 0+2\times 0.42+3\times 0.23\\ +4\times 0.21+5\times 0.09+6\times 0.03\\ +7\times 0.02\\ =3.14\end{array}$

Now,

Note that

The mean number of people in a family is greater than the mean number of people in a household.

Since the household can be smaller than families.

Thus,

It makes sense that all families have at least 2 people and all households have at least 1 person.

(c)

To determine

Relevance for the difference in standard deviation of two random variables.

Answer to Problem 19E

There can be one individual in a household, but in a family there should be more than one individual.

Explanation of Solution

Given information:

H : the number of people in randomly selected U.S. household

F : the number of people in randomly selected U.S. family

Distributions of household size and family size in U.S:

  

Histograms for F and H :

  

Standard deviation of two random variables,

For H :

  ${\sigma }_H=1.421$

For F :

  ${\sigma }_F=1.249$

From Part (a),

We conclude that

The spread of the household distribution was greater than the spread of the family distribution due to wider histogram of the household distribution.

According to the statement,

The standard deviation of household is greater than the standard deviation of family.

Thus,

The standard deviation confirms the conclusion.

Moreover,

A household can contain one individual but a family should always contain more than one individual.

Thus,

There are more possible values for the number of individuals in a household which makes its standard deviation greater.