
Concept explainers
A single bead can slide with negligible friction on a stiff wire that has been bent into a circular loop of radius 15.0 cm as shown in Figure P6.48. The circle is always in a vertical plane and rotates steadily about its vertical diameter with a period of 0.450 s. The position of the bead is described by the angle θ that the radial line, from the center of the loop to the bead, makes with the vertical. (a) At what angle up from the bottom of the circle can the bead slay motionless relative to the turning circle? (b) What If? Repeat the problem, this time taking the period of the circle’s rotation as 0.850 s. (c) Describe how the solution to part (b) is different from the solution to part (a). (d) For any period or loop size, is there always an angle at which the bead can stand still relative to the loop? (e) Are there ever more than two angles? Arnold Arons suggested the idea for this problem.
Figure P6.48
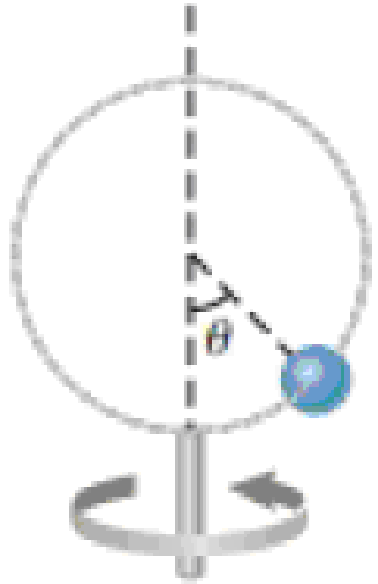
(a)
The angle from the bottom of the circle for which the bead can stay motionless.
Answer to Problem 68CP
The angles from the bottom of the circle for which the bead can stay motionless are
Explanation of Solution
Given info: The radius of the circular loop is
The acceleration due to gravity is
The rough sketch of the force body diagram of the situation is shown below,
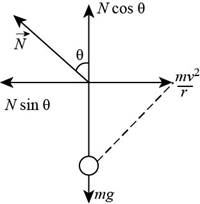
Figure (1)
The bead moves in a circle,
Here,
The speed of the bead is,
Here,
From the figure (1) the net force in
Here,
The net force in
Substitute
Substitute
The two possible solutions are,
and,
Substitute
Conclusion:
Therefore, the angles from the bottom of the circle for which the bead can stay motionless are
(b)
The angles from the bottom of the circle for which the bead can stay motionless for the time period as
Answer to Problem 68CP
The only one possible angle from the bottom of the circle for which the bead can stay motionless for time period
Explanation of Solution
Given info: The radius of the circular loop is
The acceleration due to gravity is
Form the part (a) equation (1).
The possible solutions are,
and,
Substitute
The above value is not possible.
Conclusion:
Therefore, the only one possible angle from the bottom of the circle for which the bead can stay motionless at time period
(c)
The difference between the solution of the part (a) and part (b).
Answer to Problem 68CP
The part (b) has only one solution as the time period is very large.
Explanation of Solution
Given info: The radius of the circular loop is
Form equation (1)
The possible solutions are,
and,
As the second solution depends directly on the square of the amplitude of the time period so, as the time period increases the value of
Conclusion:
Therefore, the part (b) has only one solution as the time period is very large.
(d)
The angle at which the bead can stand still relative to the loop.
Answer to Problem 68CP
The angle for which condition
Explanation of Solution
Given info: The radius of the circular loop is
Form equation (1)
The possible solutions are,
and,
As the range of the cosine function is
So, the value of the cosine of the angle is always less than
Conclusion:
Therefore, for the condition
(e)
Whether there are more than two angles.
Answer to Problem 68CP
The number of possible angles are
Explanation of Solution
Given info: The radius of the circular loop is
Form equation (1)
The possible solutions are,
and,
Form the above expression the second solution depends on time period, acceleration due to gravity and the radius of the hoop and for a given case the parameters has only one value so the second solution has only one answer.
Conclusion:
Therefore, the number of possible angles are
Want to see more full solutions like this?
Chapter 6 Solutions
Physics for Scientists and Engineers with Modern Physics, Technology Update
Additional Science Textbook Solutions
College Physics: A Strategic Approach (3rd Edition)
Campbell Biology (11th Edition)
Human Biology: Concepts and Current Issues (8th Edition)
Introductory Chemistry (6th Edition)
Fundamentals Of Thermodynamics
- What is the force (in N) on the 2.0 μC charge placed at the center of the square shown below? (Express your answer in vector form.) 5.0 με 4.0 με 2.0 με + 1.0 m 1.0 m -40 με 2.0 μCarrow_forwardWhat is the force (in N) on the 5.4 µC charge shown below? (Express your answer in vector form.) −3.1 µC5.4 µC9.2 µC6.4 µCarrow_forwardAn ideal gas in a sealed container starts out at a pressure of 8900 N/m2 and a volume of 5.7 m3. If the gas expands to a volume of 6.3 m3 while the pressure is held constant (still at 8900 N/m2), how much work is done by the gas? Give your answer as the number of Joules.arrow_forward
- The outside temperature is 25 °C. A heat engine operates in the environment (Tc = 25 °C) at 50% efficiency. How hot does it need to get the high temperature up to in Celsius?arrow_forwardGas is compressed in a cylinder creating 31 Joules of work on the gas during the isothermal process. How much heat flows from the gas into the cylinder in Joules?arrow_forwardThe heat engine gives 1100 Joules of energy of high temperature from the burning gasoline by exhausting 750 Joules to low-temperature . What is the efficiency of this heat engine in a percentage?arrow_forward
- L₁ D₁ L₂ D2 Aluminum has a resistivity of p = 2.65 × 10 8 2. m. An aluminum wire is L = 2.00 m long and has a circular cross section that is not constant. The diameter of the wire is D₁ = 0.17 mm for a length of L₁ = 0.500 m and a diameter of D2 = 0.24 mm for the rest of the length. a) What is the resistance of this wire? R = Hint A potential difference of AV = 1.40 V is applied across the wire. b) What is the magnitude of the current density in the thin part of the wire? Hint J1 = c) What is the magnitude of the current density in the thick part of the wire? J₂ = d) What is the magnitude of the electric field in the thin part of the wire? E1 = Hint e) What is the magnitude of the electric field in the thick part of the wire? E2 =arrow_forwardplease helparrow_forwardA cheetah spots a gazelle in the distance and begins to sprint from rest, accelerating uniformly at a rate of 8.00 m/s^2 for 5 seconds. After 5 seconds, the cheetah sees that the gazelle has escaped to safety, so it begins to decelerate uniformly at 6.00 m/s^2 until it comes to a stop.arrow_forward
- A projectile is fired with an initial speed of 40.2 m/s at an angle of 35.0 degree above the horizontal on a long flat firing range. Determine. please help and show work for them so i can understand.arrow_forwardpls helparrow_forwardJ K L The graph in the figure shows the position of an object as a function of time. The letters H-L represent particular moments of time. At which moments shown (H, I, etc.) is the speed of the object the greatest? + Position H I K Timearrow_forward
 Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University





