University Physics with Modern Physics (14th Edition)
14th Edition
ISBN: 9780321973610
Author: Hugh D. Young, Roger A. Freedman
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 6, Problem 6.35E
Three identical 8.50-kg masses are hung by three identical springs (Fig. E6.35). Each spring has a force constant of 7.80 kN/m and was 12.0 cm long before any masses were attached to it (a) Draw a free-body diagram of each mass. (b) How long is each spring when hanging as shown? (Hint: First isolate only the bottom mass. Then treat the bottom two masses as a system. Finally, treat all three masses as a system.)
Figure E6.35
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A 6.50 ✕ 105 kg subway train is brought to a stop from a speed of 0.500 m/s in 0.600 m by a large spring bumper at the end of its track. What is the force constant k of the spring (in N/m)?
In the vault event, the gymnast begins her routine by jumping on a springboard, a platform with springs underneath. In one vault, a 45 kg gymnast jumps 0.60 m above the springboard’s surface. She then lands on the springboard, which compresses it. What is the maximum compression of the springboard? How much time does it take for the board to fully compress? The spring constant of the board is 50,000 N/m.
A 5.00 ✕ 105 kg subway train is brought to a stop from a speed of 0.500 m/s in 0.300 m by a large spring bumper at the end of its track. What is the force constant k of the spring (in N/m)?
N/m
Chapter 6 Solutions
University Physics with Modern Physics (14th Edition)
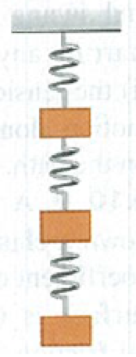
Ch. 6.1 - An electron moves in a straight line toward the...Ch. 6.2 - Rank the following bodies in order of their...Ch. 6.3 - In Example 5.20 (Section 5.4) we examined a...Ch. 6.4 - The air surrounding an airplane in flight exerts a...Ch. 6 - The sign of many physical quantities depends on...Ch. 6 - An elevator is hoisted by its cables at constant...Ch. 6 - A rope tied to a body is pulled, causing the body...Ch. 6 - If it takes total work W to give an object a speed...Ch. 6 - If there is a net nonzero force on a moving...Ch. 6 - In Example 5.5 (Section 5.1), how does the work...
Ch. 6 - In the conical pendulum of Example 5.20 (Section...Ch. 6 - For the cases shown in Fig. Q6.8, the object is...Ch. 6 - A force F is in the x-direction and has a...Ch. 6 - Does a cars kinetic energy change more when the...Ch. 6 - A falling brick has a mass of 1.5 kg and is moving...Ch. 6 - Can the total work done on an object during a...Ch. 6 - A net force acts on an object and accelerates it...Ch. 6 - A truck speeding down the highway has a lot of...Ch. 6 - You are holding a briefcase by the handle, with...Ch. 6 - When a book slides along a tabletop. the force of...Ch. 6 - Time yourself while running up a flight of steps,...Ch. 6 - Fractured Physics. Many terms from physics are...Ch. 6 - An advertisement for a portable electrical...Ch. 6 - A car speeds up while the engine delivers constant...Ch. 6 - Consider a graph of instantaneous power versus...Ch. 6 - A nonzero net force acts on an object. Is it...Ch. 6 - When a certain force is applied to an ideal...Ch. 6 - If work W is required to stretch a spring a...Ch. 6 - You push your physics book 1.50 m along a...Ch. 6 - Using a cable with a tension of 1350 N, a tow...Ch. 6 - A factory worker pushes a 30.0-kg crate a distance...Ch. 6 - Suppose the worker in Exercise 6.3 pushes downward...Ch. 6 - A 75.0-kg painter climbs a ladder that is 2.75 m...Ch. 6 - Two tugboats pull a disabled supertanker. Each tug...Ch. 6 - Two blocks are connected by a very light string...Ch. 6 - A loaded grocery cart is rolling across a parking...Ch. 6 - A 0.800-kg ball is tied to the end of a string...Ch. 6 - A 12.0-kg package in a mail-sorting room slides...Ch. 6 - A 128.0-N carton is pulled up a frictionless...Ch. 6 - A boxed 10.0-kg computer monitor is drugged by...Ch. 6 - A large crate sits on the floor of a warehouse....Ch. 6 - You apply a constant force F=(68.0N)i+(36.0N)j to...Ch. 6 - You are holding a briefcase by the handle, with...Ch. 6 - When a book slides along a tabletop, the force of...Ch. 6 - Time yourself while running up a flight of steps,...Ch. 6 - Fractured Physics. Many terms from physics are...Ch. 6 - Meteor Crater. About 50,000 years ago, a meteor...Ch. 6 - A 4.80-kg watermelon is dropped from rest from the...Ch. 6 - Use the work-energy theorem to solve each of these...Ch. 6 - Use the work-energy theorem to solve each of these...Ch. 6 - You are a member of an Alpine Rescue Team. You...Ch. 6 - You throw a 3.00-N rock vertically into the air...Ch. 6 - A sled with mass 12.00 kg moves in a straight line...Ch. 6 - A mass m slides down a smooth inclined plane from...Ch. 6 - A 12-pack of Omni-Cola (mass 4.30 kg) is initially...Ch. 6 - A soccer ball with mass 0.420 kg is initially...Ch. 6 - A little red wagon with mass 7.00 kg moves in a...Ch. 6 - A block of ice with mass 2.00 kg slides 1.35 m...Ch. 6 - Stopping Distance. A car is traveling on a level...Ch. 6 - A 30.0-kg crate is initially moving with a...Ch. 6 - BIO Heart Repair. A surgeon is using material from...Ch. 6 - To stretch a spring 3.00 cm from its unstretched...Ch. 6 - Three identical 8.50-kg masses are hung by three...Ch. 6 - A child applies a force F parallel to the x-axis...Ch. 6 - Suppose the sled in Exercise 6.36 is initially at...Ch. 6 - A spring of force constant 300.0 N/m and...Ch. 6 - A 6.0-kg box moving at 3.0 m/s on a horizontal,...Ch. 6 - Leg Presses. As part of your daily workout, you...Ch. 6 - (a) In Example 6.7 (Section 6.3) it was calculated...Ch. 6 - A 4.00-kg block of ice is placed against a...Ch. 6 - A force F is applied to a 2.0-kg, radio-controlled...Ch. 6 - Suppose the 2.0-kg model car in Exercise 6.43 is...Ch. 6 - Prob. 6.45ECh. 6 - Half or a Spring. (a) Suppose you cut a massless...Ch. 6 - A small glider is placed against a compressed...Ch. 6 - An ingenious bricklayer builds a device for...Ch. 6 - CALC A force in the +x-direction with magnitude...Ch. 6 - A crate on a motorized cart starts from rest and...Ch. 6 - How many joules of energy does a 100-watt light...Ch. 6 - BIO Should You Walk or Run? It is 5.0 km from your...Ch. 6 - Magnetar. Oil December 27, 2004, astronomers...Ch. 6 - A 20.0-kg rock is sliding on a rough, horizontal...Ch. 6 - A tandem (two-person) bicycle team must overcome a...Ch. 6 - When its 75-kW (100-hp) engine is generating full...Ch. 6 - Working Like a Horse. Your job is to lift 30-kg...Ch. 6 - An elevator has mass 600 kg, not including...Ch. 6 - A ski tow operates on a 15.0 slope of length 300...Ch. 6 - You are applying a constant horizontal force F =...Ch. 6 - BIO While hovering, a typical flying insect...Ch. 6 - CALC A balky cow is leaving the barn as you try...Ch. 6 - A luggage handler pulls a 20.0-kg suitcase up a...Ch. 6 - Chin-ups. While doing a chin-up, a man lifts his...Ch. 6 - Consider the blocks in Exercise 6.7 as they move...Ch. 6 - A 5.00-kg package slides 2.80 m down a long ramp...Ch. 6 - CP BIO Whiplash Injuries. When a car is hit from...Ch. 6 - CALC A net force along the x-axis that has...Ch. 6 - CALC Varying Coefficient of Friction. A box is...Ch. 6 - CALC Consider a spring that does not obey Hookes...Ch. 6 - CP A small block with Figure P6.71 a mass of...Ch. 6 - CALC Proton Bombardment. A proton with mass 1.67 ...Ch. 6 - You are asked to design spring bumpers for the...Ch. 6 - You and your bicycle have combined mass 80.0 kg....Ch. 6 - A 2.50-kg textbook is forced against a horizontal...Ch. 6 - The spring of a spring gun has force constant k =...Ch. 6 - One end of a horizontal spring with force constant...Ch. 6 - One end of a horizontal spring with force constant...Ch. 6 - A 5.00-kg block is moving at 0 = 6.00 m/s along a...Ch. 6 - A physics professor is pushed up a ramp inclined...Ch. 6 - Consider the system shown in Fig. P6.81. The rope...Ch. 6 - Consider the system shown in Fig. P6.81. The rope...Ch. 6 - On an essentially frictionless, horizontal ice...Ch. 6 - BIO All birds, independent of their size, must...Ch. 6 - A pump is required to lift 800 kg of water (about...Ch. 6 - The Grand Coulee Dam is 1270 m long and 170 m...Ch. 6 - A physics student spends part of her day walking...Ch. 6 - CALC An object has several forces acting on it....Ch. 6 - BIO Power of the Human Heart. The human heart is a...Ch. 6 - DATA Figure P6.90 shows the results of measuring...Ch. 6 - DATA In a physics lab experiment, one end of a...Ch. 6 - DATA For a physics lab experiment, four classmates...Ch. 6 - CALC A Spring with Mass. We usually ignore the...Ch. 6 - CALC An airplane in flight is subject to an air...Ch. 6 - BIO ENERGY OF LOCOMOTION. On flat ground, a 70-kg...Ch. 6 - BIO ENERGY OF LOCOMOTION. On flat ground, a 70-kg...Ch. 6 - BIO ENERGY OF LOCOMOTION. On flat ground, a 70-kg...
Additional Science Textbook Solutions
Find more solutions based on key concepts
What were the major microbiological interests of Martinus Beijerinck and Sergei Winogradsky? It can be said tha...
Brock Biology of Microorganisms (15th Edition)
Modified True/False 3. __________ Aquatic microorganisms are more prevalent near the surface than at the bottom...
Microbiology with Diseases by Body System (5th Edition)
42. Two of the emission wavelengths in the hydrogen emission spectrum are 656 nm and 486 nm. One of these is du...
Introductory Chemistry (6th Edition)
Choose the best answer to each of the following. Explain your reasoning. What do we conclude if a planet has fe...
Cosmic Perspective Fundamentals
15. A good scientific hypothesis is based on existing evidence and leads to testable predictions. What hypothes...
Campbell Biology: Concepts & Connections (9th Edition)
Why are the top predators in food chains most severely affected by pesticides such as DDT?
Campbell Essential Biology with Physiology (5th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Why is the following situation impossible? In a new casino, a supersized pinball machine is introduced. Casino advertising boasts that a professional basketball player can lie on top of the machine and his head and feet will not hang off the edge! The hall launcher in the machine sends metal halls up one side of the machine and then into play. The spring in the launcher (Fig. P7.44) has a force constant of 1.20 N/cm. The surface on which the ball moves is inclined = 10.0 with respect to the horizontal. The spring is initially compressed its maximum distance d = 5.00 cm. A ball of mass 100 g is projected into play by releasing the plunger. Casino visitors find the play of the giant machine quite exciting. Figure P7.44arrow_forwardWhy is the following situation impossible? In a new casino, a supersized pinball machine is introduced. Casino advertising boasts that a professional basketball player can lie on top of the machine and his head and feet will not hang off the edge! The ball launcher in the machine sends metal balls up one side of the machine and then into play. The spring in the launcher (Fig. P6.60) has a force constant of 1.20 N/cm. The surface on which the ball moves is inclined = 10.0 with respect to the horizontal. The spring is initially compressed its maximum distance d = 5.00 cm. A ball of mass 100 g is projected into play by releasing the plunger. Casino visitors find the play of the giant machine quite exciting.arrow_forwardAn inclined plane of angle = 20.0 has a spring of force constant k = 500 N/m fastened securely at the bottom so that the spring is parallel to the surface as shown in Figure P6.61. A block of mass m = 2.50 kg is placed on the plane at a distance d = 0.300 m from the spring. From this position, the block is projected downward toward the spring with speed v = 0.750 m/s. By what distance is the spring compressed when the block momentarily comes to rest?arrow_forward
- A 6 000-kg freight car rolls along rails with negligible friction. The car is brought to rest by a combination of two coiled springs as illustrated in Figure P6.27 (page 188). Both springs are described by Hookes law and have spring constants k1 = 1 600 N/m and k2, = 3 400 N/m. After the first spring compresses a distance of 30.0 cm, the second spring acts with the first to increase the force as additional compression occurs as shown in the graph. The car comes to rest 50.0 cm after first contacting the two-spring system. Find the cars initial speed.arrow_forwardA block of mass 0.250 kg is placed on top of a light, vertical spring of force constant 5 000 N/m and pushed downward so that the spring is compressed by 0.100 m. After the block is released from rest, it travels upward and then leaves the spring. To what maximum height above the point of release does it rise?arrow_forwardAssume that the force of a bow on an arrow behaves like the spring force. In aiming the arrow, an archer pulls the bow back 50 cm and holds it in position with a force of 150 N. If the mass of the arrow is 50 g and the “spring” is massless, what is the speed of the arrow immediately after it leaves the bow?arrow_forward
- A small 0.65-kg box is launched from rest by a horizontal spring as shown in Figure P9.50. The block slides on a track down a hill and comes to rest at a distance d from the base of the hill. The coefficient of kinetic friction between the box and the track is 0.35 along the entire track. The spring has a spring constant of 34.5 N/m, and is compressed 30.0 cm with the box attached. The block remains on the track at all times. a. What would you include in the system? Explain your choice. b. Calculate d. c. Compare your answer with your answer to Problem 50 if you did that problem.arrow_forwardAt 220 m, the bungee jump at the Verzasca Dam in Locarno, Switzerland, is one of the highest jumps on record. The length of the elastic cord, which can be modeled as having negligible mass and obeying Hookes law, has to be precisely tailored to each jumper because the margin of error at the bottom of the dam is less than 10.0 m. Kristin prepares for her jump by first hanging at rest from a 10.0-m length of the cord and is observed to stretch the rope to a total length of 12.5 m. a. What length of cord should Kristin use for her jump to be exactly 220 m? b. What is the maximum acceleration she will experience during her jump?arrow_forwardA light spring with spring constant 1 200 N/m is hung from an elevated support. From its lower end hangs a second light spring, which has spring constant 1 800 N/m. An object of mass 1.50 kg is hung at rest from the lower end of the second spring. (a) Find the total extension distance of the pair of springs. (b) Find the effective spring constant of the pair of springs as a system. We describe these springs as in series.arrow_forward
- A 1.00-kg object slides to the right on a surface having a coefficient of kinetic friction 0.250 (Fig. P8.62a). The object has a speed of vi = 3.00 m/s when it makes contact with a light spring (Fig. P8.62b) that has a force constant of 50.0 N/m. The object comes to rest after the spring has been compressed a distance d (Fig. P8.62c). The object is then forced toward the left by the spring (Fig. P8.62d) and continues to move in that direction beyond the spring's unstretched position. Finally, the object comes to rest a distance D to the left of the unstretched spring (Fig. P8.62e). Find (a) the distance of compression d, (b) the speed vat the unstretched posi-tion when the object is moving to the left (Fig. P8.624), and (c) the distance D where the abject comes to rest. Figure P8.62arrow_forwardYou are lying in your bedroom, resting after doing your physics homework. As you stare at your ceiling, you come up with the idea for a new game. You grab a dart with a sticky nose and a mass of 19.0 g. You also grab a spring that has been lying on your desk from some previous project. You paint a target pattern on your ceiling. Your new game is to place the spring vertically on the floor, place the sticky-nose dart facing upward on the spring, and push the spring downward until the coils all press together, as on the right in Figure P7.26. You will then release the spring, firing the dart up toward the target on your ceiling, where its sticky nose will make it hang from the ceiling. The spring has an uncompressed end-to-end length of 5.00 cm, as shown on the left in Figure P7.26, and can be compressed to an end-to-end length of 1.00 cm when the coils are all pressed together. Before trying the game, you hold the upper end of the spring in one hand and hang a bundle of ten identical darts from the lower end of the spring. The spring extends by 1.00 cm due to the weight of the darts. You are so excited about the new game that, before doing a test of the game, you run out to gather your friends to show them. When your friends are in your room watching and you show them the first firing of your new game, why are you embarrassed?arrow_forwardConsider the data for a block of mass m = 0.250 kg given in Table P16.59. Friction is negligible. a. What is the mechanical energy of the blockspring system? b. Write expressions for the kinetic and potential energies as functions of time. c. Plot the kinetic energy, potential energy, and mechanical energy as functions of time on the same set of axes. Problems 5965 are grouped. 59. G Table P16.59 gives the position of a block connected to a horizontal spring at several times. Sketch a motion diagram for the block. Table P16.59arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
8.01x - Lect 11 - Work, Kinetic & Potential Energy, Gravitation, Conservative Forces; Author: Lectures by Walter Lewin. They will make you ♥ Physics.;https://www.youtube.com/watch?v=9gUdDM6LZGo;License: Standard YouTube License, CC-BY