
(a)
Interpretation:
Poles and zeros of the given transfer function are to be plotted on a complex plane.
Concept introduction:
For any transfer function
For any transfer function
Answer to Problem 6.1E
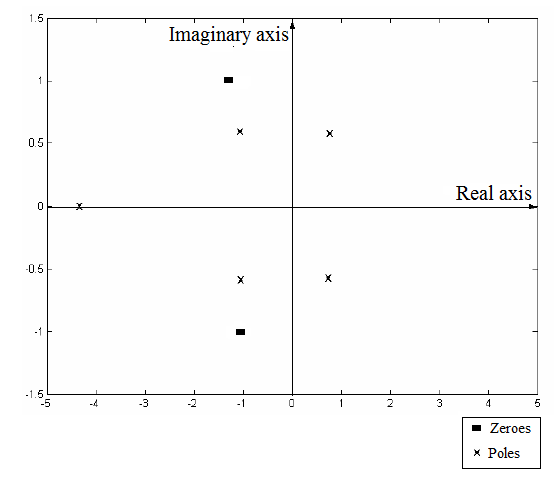
The plot of the poles and zeros of the given transfer function on the complex plane as:
Explanation of Solution
Given information:
The given transfer function is:
For the given transfer function, the numerator polynomial is:
To calculate the zeros of the given transfer function, equation this polynomial to zero and calculate its roots using MATLAB commands as shown below:
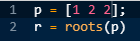
The compiler will generate its roots as:
These are the zeros of the given transfer function.
For the given transfer function, the denominator polynomial is:
To calculate the poles of the given transfer function, equation this polynomial to zero and calculate its roots using MATLAB commands as shown below:
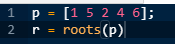
The compiler will generate its roots as:
These are the poles of the given transfer function.
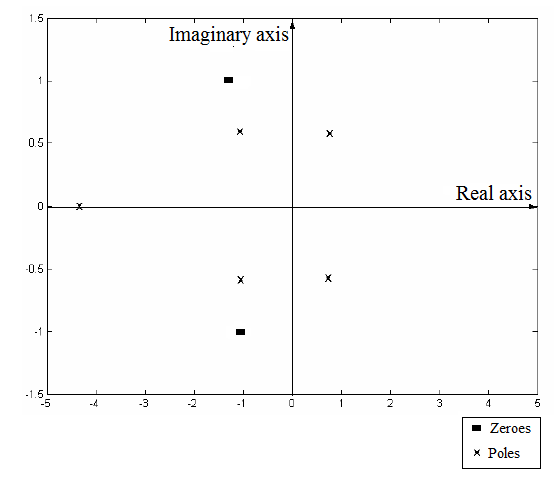
Now, plot these poles and zeros on the complex plane as:
(b)
Interpretation:
The conclusion regarding the output modes for any input changes is to be determined from the location of poles in the complex plane.
Concept introduction:
For any transfer function
For any transfer function
The complex plane is divided into two halves: Left Half Plane and Right Half Plane. The Left Half Plane represents the stable region and the Right Half Plane represents the unstable region.
Answer to Problem 6.1E
Any change in the input of the process will lead to the unbounded and unstable output as two of the poles of the given transfer function lie in the Right Half Plane.
Explanation of Solution
Given information:
The given transfer function is:
From part (a), the plot of poles and zeros of the given polynomial is:
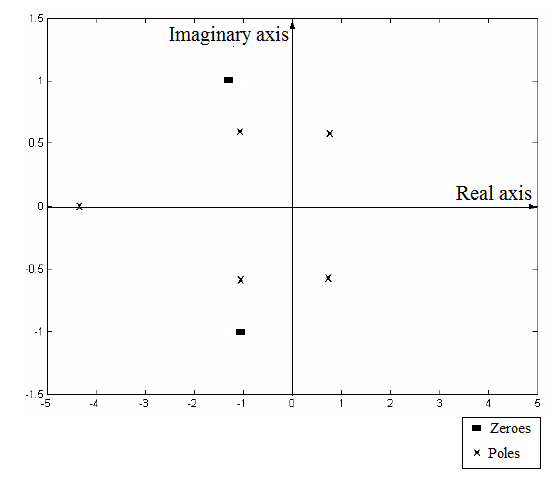
From this plot, two of the poles lie in the Right Half Plane of the complex plane. This makes the process output unstable. Therefore, any change in the input of the process will lead to unbounded and unstable output.
(c)
Interpretation:
The output response for the unit step change in the input for the given transfer function is to be plotted and its correctness to the analysis of the output mode made in part (b) is to be done.
Concept introduction:
For any transfer function
For any transfer function
The complex plane is divided into two halves: Left Half Plane and Right Half Plane. The Left Half Plane represents the stable region and the Right Half Plane represents the unstable region.
Answer to Problem 6.1E
The response of the given transfer function for a unit step change in the input is:
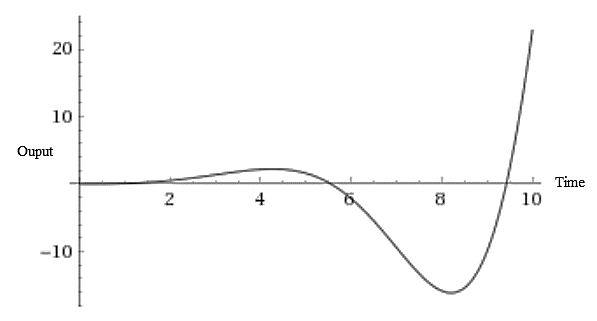
The output response of the process is unstable and unbounded for the step-change in the input which agrees with the analysis done in part (b).
Explanation of Solution
Given information:
The given transfer function is:
For a unit step change in the input, the value of
Substitute this value of
The plot of the response of this transfer function using the online tool will be:
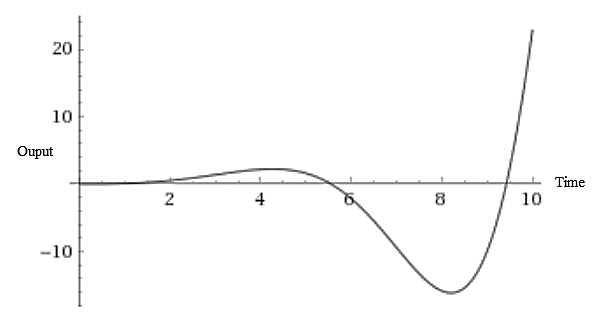
In part (b), it was analyzed that the poles pair in the Right Half Plane makes the system output unbounded and stable. From the response plot shown above, this analysis is correct as the output response of the process is unstable and unbounded for the step-change in the input.
Want to see more full solutions like this?
Chapter 6 Solutions
Process Dynamics and Control, 4e
- Creep compliance J(t) An amorphous polymer has Tg = 100 °C. A creep modulus of 1/J = 1 GPa was measured after t₁ = 1 h at T₁ = 90 °C. Suppose that log 10 a (T) = 17.5(T-Tg) 52+(T-Tg) 1 for this material. What is the shift factor a at T = T₁ relative to the reference Tg? What is the time t₂ required to reach a modulus of 1 GPa at T2 = 80 °C? TR = T = 100 °C |J(t) = 1 GPa-1 + log a(T₁) T₁ = 75 °C T₂ = 50 °C log tr log t₁ log t log t₂ = ?arrow_forwardA 0.45 mol/kg aqueous solution of 3-(methylamino)propylamine and 1-methylpiperazine (1:1 molar) flows at 0.5 g/s through a 2.5 m horizontal stainless steel coil (inner diameter 1.2 mm), entering at 358.15 K and 22 MPa and exiting at 20 MPa. A constant wall heat flux of 28 W is applied. Local density and isobaric heat capacity are obtained through from the Benedict–Webb–Rubin equation of state, with a 3% increase in heat capacity to account for wall sorption. Dynamic viscosity is obtained using the Green-Kubo relation with a given integral value of 2.1 × 10⁻¹⁰ Pa².s, and thermal conductivity is assumed constant. The local Nusselt number is corrected for thermal development using Nu(x) = 3.66 + (0.065 · Gz(x)^0.7) / (1 + 0.04 · Gz(x)^0.7), where Gz(x) = D · Re(x) · Pr(x) / x. Through a spatially resolved numerical integration of the 1D steady-state energy equation and determine the outlet temperature (K).arrow_forwardA pilot process is being planned to produce antibiotic P. Antibiotic P is a compound secreted by microorganism A during the stationary phase. To produce P, substrate S is required. The growth of microorganism A follows the Monod equation, with a maximum specific growth rate $\mu_m = 1 h^{-1}$ and a half-saturation constant $K_s = 700\ mg/L$.The pilot process uses a chemostat with a working volume of $1000\ L$. In this chemostat, the outflow is processed to separate microorganisms, which are then concentrated tenfold and recycled. A sterile medium containing $15\ g/L$ of substrate is supplied at a flow rate of $100\ L/h$, while the recycled flow (concentrated) contains $5\ g/L$ and is also fed into the chemostat.Microorganism A yields $0.5\ g$ of biomass per $1\ g$ of substrate consumed $(Y^M_{X/S} = 0.5\ g\ A/g\ S)$, and its death rate $(k_d)$ is negligible. Additionally, $1\ g$ of microorganism A produces $0.05\ g$ of antibiotic P per hour $(q_P = 0.05 g\ P/h\cdot g\ A)$, and $1\ g$…arrow_forward
- In the production of ethyl acetate via reactive distillation, the column operates at 5 bar with an equimolar feed (ethanol + acetic acid) at 80°C. The reaction follows: \[CH_3COOH + C_2H_5OH \rightleftharpoons CH_3COOC_2H_5 + H_2O \quad (K_{eq} = 4.2 \text{ at } 80°C)\] Given: - NRTL parameters for all binary pairs - Tray efficiency = 65% - Vapor-liquid equilibrium exhibits positive azeotrope formation Calculate the exact minimum reflux ratio required to achieve 98% ethyl acetate purity in the distillate, assuming: 1) The reaction reaches equilibrium on each tray 2) The heavy key component is waterarrow_forwardIn a multi-stage distillation column designed to separate a binary mixture of ethanol and water, the mass flow rate of the feed entering the column is \( F \), and the distillate product flow rate is \( D \). The reflux ratio \( R \) is defined as the ratio of the liquid returned to the column to the distillate flow rate. For the ideal case, where the column operates at maximum efficiency, determine the **minimum reflux ratio** \( R_{\text{min}} \) when the relative volatility \( \alpha = 1.5 \).arrow_forwardQ2: Draw the layout of a basic asynchronous 32k * 8 SRAM.arrow_forward
- A distillation column with 100 kmol/h feed of 50% A and 50% B produces a distillate product with xD = 0.95 and a bottom stream with xbot = 0.04 of the more volatile species A. CMO is valid and the equilibrium data is given by y = 2.4x/1 + 1.4x a) If the feed is saturated liquid, determine the minimum reflux ratio b) If the feed is saturated vapor, determine the minimum reflux ratioarrow_forwardA distillation column with 100 kmol/h feed of 60% A and 40% B produces a distillate product with xD = 0.98 and a bottom stream with xbot = 0.02 of the more volatile species A. CMO is valid and the equilibrium data is given by y = 2.2x/1+1.2x a) If the reflux ratio R is 2, determine (numerically) the composition (y) of the vapor stream entering the top equilibrium plate.__________b) If R = 2 and q = 0.6, determine the liquid flow rate in the stripping section of the column__________c) If q = 0, the minimum reflux ratio isarrow_forwardNatural gas having a specific gravity relative to air of 0.60 and a viscosity of 0.011 cP is flowing through a 6-in. Schedule 40 pipe in which is installed a standard sharp-edged orifice equipped with flange taps. The gas is at 100°F and 20lb/in? abs at the upstream tap. The manometer reading is 46.3 in. of water at 60°F. The ratio of specific heats for natural gas is 1.30. The diameter of the orifice is 2.00 in. Calculate the rate of flow of gas through the line in cubic feet.arrow_forward
- صورة من s94850121arrow_forward11:01 ☑ canvas.ucsd.edu 口 : ... Page 1 > of 2 Q - ZOOM + 4. Consider the two separate sets of measured data for a silt-loam soil measured by Mualem (1976): (1) suction versus water content, and (2) suction versus relative permeability of unsaturated soil, k/ks. Assume that 0s 0.396, 0res = 0.131, and Ks=5.74×10-7 m/s. a. Using the method of least squares in Excel, compute the best-fit values for αNG (kPa¹) and nvg for the van Genuchten (1980) relationship for data set # 1 (assume m = 1-1/nvG). See the example spreadsheet in the homework folder under the files section of Canvas for help in performing this calculation. b. Repeat part (a) and estimate the λ and ac parameters for the Brooks and Corey (1964) SWRC for data set #1. Note that you may need to include an "if" statement at the air entry suction. c. Plot the data for the SWRC versus the fitted van Genuchten (1980) and Brooks and Corey (1964) curves. Which relationship matches the capillary pressure data better (BC or VG)? Explain…arrow_forwardSolve h.w 6arrow_forward
 Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education
Introduction to Chemical Engineering Thermodynami...Chemical EngineeringISBN:9781259696527Author:J.M. Smith Termodinamica en ingenieria quimica, Hendrick C Van Ness, Michael Abbott, Mark SwihartPublisher:McGraw-Hill Education Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...Chemical EngineeringISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
Elements of Chemical Reaction Engineering (5th Ed...Chemical EngineeringISBN:9780133887518Author:H. Scott FoglerPublisher:Prentice Hall
 Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning
Industrial Plastics: Theory and ApplicationsChemical EngineeringISBN:9781285061238Author:Lokensgard, ErikPublisher:Delmar Cengage Learning Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The
Unit Operations of Chemical EngineeringChemical EngineeringISBN:9780072848236Author:Warren McCabe, Julian C. Smith, Peter HarriottPublisher:McGraw-Hill Companies, The





