
Concept explainers
(a)
The tangent elastic modulus.
(a)
Answer to Problem 6.19P
The tangent elastic modulus at zero strain is
Explanation of Solution
Formula Used:
Write the expression for the tangent elastic modulus.
Here,
Calculation:
Refer Figure 6.16 “Tensile stress-strain diagram for four different type of materials” from the book “Material Science and Engineering Properties”.
The value of change is stress for PMMA is
Substitute
Conclusion:
Thus, the tangent elastic modulus at zero strain is
(b)
The yield stress of PMMA.
(b)
Answer to Problem 6.19P
The yield stress for PMMA is
Explanation of Solution
Calculation:
Refer Figure 6.16 “Tensile stress-strain diagram for four different type of materials” from the book “Material Science and Engineering Properties”.
The tensile stress diagram for PMMA is shown in figure below.
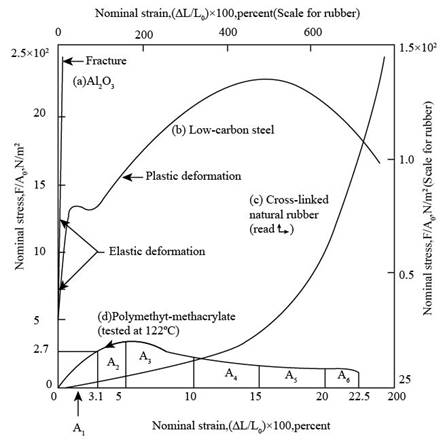
Figure (1)
The value of the yield stress for PMMA is
Conclusion:
Thus, the yield stress for PMMA is
(c)
The resilience of PMMA.
(c)
Answer to Problem 6.19P
The resilience of PMMA is
Explanation of Solution
Formula Used:
Write the expression for the resilience.
Here,
Calculation:
Substitute
Conclusion:
Thus, the resilience of PMMA is
(d)
The ultimate tensile strength of PMMA.
(d)
Answer to Problem 6.19P
The ultimate tensile strength for PMMA is
Explanation of Solution
Calculation:
The ultimate tensile strength in a stress-strain diagram is obtained by observation of the highest point that is reached by the curve after which the necking of curve starts.
Refer Figure 6.16 “Tensile stress-strain diagram for four different type of materials” from the book “Material Science and Engineering Properties”.
The value of the ultimate tensile strength for PMMA is
Conclusion:
Thus, the ultimate tensile strength for PMMA is
(e)
The toughness of PMMA.
(e)
Answer to Problem 6.19P
The toughness of PMMA is
Explanation of Solution
Formula Used:
Write the expression for the first area.
Here,
Write the expression for the second area.
Here,
Write the expression for the third area.
Here,
Write the expression for the fourth area.
Here,
Write the expression for the fifth area.
Here,
Write the expression for the sixth area.
Here,
Write the expression for the toughness of specimen.
Calculation:
Refer Figure 6.16 “Tensile stress-strain diagram for four different type of materials” from the book “Material Science and Engineering Properties”.
The stress strain diagram for PMMA with sub-divided area is shown below,
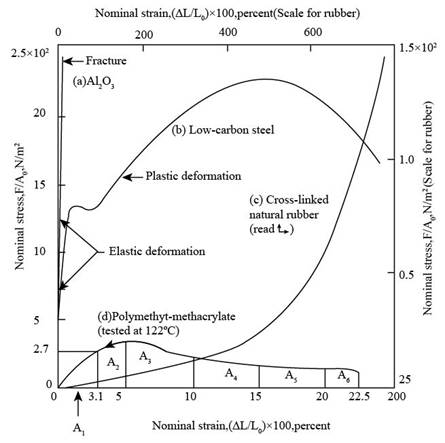
Figure (2)
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Conclusion:
Thus, the toughness of PMMA is
Want to see more full solutions like this?
Chapter 6 Solutions
Materials Science and Engineering Properties, SI Edition
- Give me a sample tension member problems with staggered bolt holes where I calculate net area using the staggered hole formula, with complete solution and answer.arrow_forwardGive me a block shear failure problem involving a bolted steel plate, and solve for nominal strength, with detailed solution and answer.arrow_forwardGive me a sample problems computing effective net area of a tension member with staggered holes, with full solution and answer. plsssarrow_forward
- Can u pls give me sample problems on steel tension member design involving gross and net area, with complete solution and final answer. Note: I just needed to reviewarrow_forward(a) Determine the Nataf model for the joint PDF fxx, (xx) of the basic (physical) random variables X₁ and X, with marginal PDF's fx(x)=e, 0≤x (Exponential distribution) fx₁ (x2)=x2e-0.5x, 0≤x (Rayleigh distribution) and correlation coefficient Pxx=0.50 Note: Use Table 6 of paper by Liu and Der Kiureghian, 1986. (b) Generate a 3D surface plot and contour plot of the joint PDF fxx, (x,x) using Matlab or any other software of your choice. (c) What is the standard deviation of X2? (d) Construct a transformation from the physical X space (defined by random variables X, and X,) to the standard normal U space (defined by the statistically independent standard normal random variables (U, and U₂), i.e., U=T(X). Also describe the inverse transform X=T(U) and the Jacobian matrices J = ди θα and Ju Ox ди (e) According to the inverse transformation X = T¹ (U) and using Matlab, generate 1,000 samples from the Nataf joint PDF fxx, (x1,x2) derived in part (a). Start by generating samples of U using a…arrow_forwardBased on the results obtained, comment on the relative importance of the body and the tails of thedistributions of R and S on the probability of failure with increasing central safety factor CSF .arrow_forward
- 1. The beam is supported by a roller constraint at B, which allows vertical displacement but resists axial load and moment. If the bar is subjected to the loading shown and constant El (L = 12 ft, E = 3100 ksi, I = 1728 in (rectangular section 12"x12"), w = 1 klf). Caution: pay attention to unit conversion between ft and in) x W B a. Sketch the deflected shape. L b. Determine the equations of the slope and the elastic curve using the coordinate x. First, solve this problem parametrically, and then substitute the numerical values for L, E, I, w at the end. There will be a significant penalty for solutions that do not calculate the slope and deflection as parametric functions. c. Specify the slope (in radians) at point A (parametrically and numerically). d. Specify the vertical displacement at point B (parametrically and numerically).arrow_forward4. EI is constant in the beam below (a = 12 ft, b = 5 ft, E = 29,000 ksi, I = 800 in¹ (W18x50), P = 2 kip): b Р C a. Sketch the deflected shape. b. Determine the equations of the slope and the elastic curve using the coordinates x1 and x2. c. For the AB segment, determine the maximum deflection and its location. Hint: at maximum deflection, the slope is zero. d. Specify the slope (in radians) and deflection at point C.arrow_forward3. EI is constant in the beam below (a = 10 ft, b = 5 ft, E = 29,000 ksi, I = 340 in (W14x34), Mo = 50 k. ft): Mo Mo a. Sketch the deflected shape. X2 b. Determine the equations of the slope and the elastic curve using the coordinates x1 and x2. Due to symmetry, only the left side is sufficient. Hint: symmetry requires the slope to be zero at mid span. c. Determine the maximum deflection. d. Specify the slope (in radians) at point A.arrow_forward
- 2. EI is constant in the beam below (L = 10 ft, E = 29,000 ksi, I = 350 in (W12x45), W = 500 lb/ft): a. Sketch the deflected shape. b. Determine the equations of the slope and the elastic curve using the coordinates x1 and X2. c. Specify the slope (in radians) and deflection at point C. d. Specify the slope (in radians) at point B. -x- L 2 W C X27 L 22 Barrow_forwardRead the paper of Khalili et al. (2004). Describe the issue raised by Jennings and Burland in using the single-value effective stress to quantify the problem of wetting-induced collapse. Use the discussion in Khalili et al. (2004) on the different ways that effective stress and yield stress change with suction to explain how wetting-induced collapse can be modeled with the single-valued effective stress. Comment on whether the soil tested by Jotisankasa (2003) would be collapsible based on the discussionarrow_forwardplease explain step by step and use the ACI codearrow_forward
 Materials Science And Engineering PropertiesCivil EngineeringISBN:9781111988609Author:Charles GilmorePublisher:Cengage Learning
Materials Science And Engineering PropertiesCivil EngineeringISBN:9781111988609Author:Charles GilmorePublisher:Cengage Learning Steel Design (Activate Learning with these NEW ti...Civil EngineeringISBN:9781337094740Author:Segui, William T.Publisher:Cengage Learning
Steel Design (Activate Learning with these NEW ti...Civil EngineeringISBN:9781337094740Author:Segui, William T.Publisher:Cengage Learning Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Construction Materials, Methods and Techniques (M...Civil EngineeringISBN:9781305086272Author:William P. Spence, Eva KultermannPublisher:Cengage Learning
Construction Materials, Methods and Techniques (M...Civil EngineeringISBN:9781305086272Author:William P. Spence, Eva KultermannPublisher:Cengage Learning



