Bundle: Physics For Scientists And Engineers With Modern Physics, Loose-leaf Version, 10th + Webassign Printed Access Card For Serway/jewett's Physics For Scientists And Engineers, 10th, Single-term
10th Edition
ISBN: 9781337888585
Author: Raymond A. Serway, John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 6, Problem 32AP
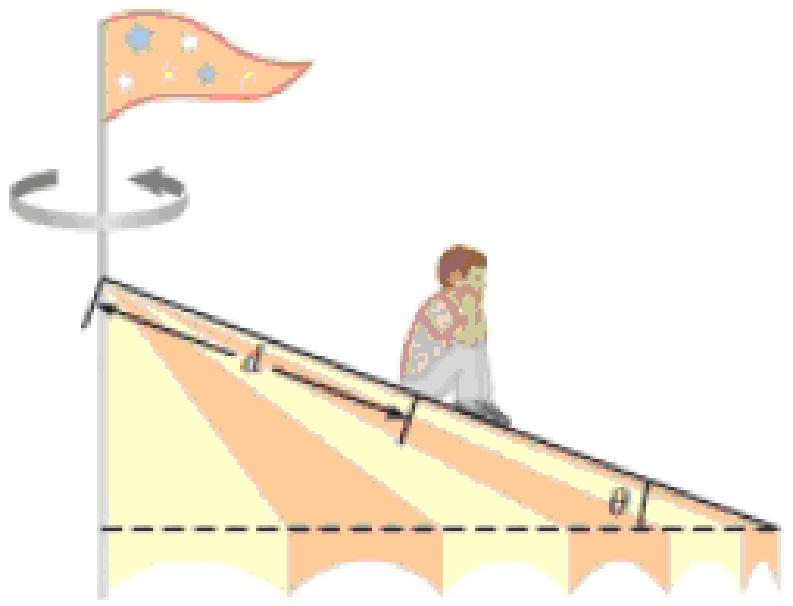
Why is the following situation impossible? A mischievous child goes to an amusement park with his family. On one ride, after a severe scolding from his mother, he slips out of his seat and climbs to the top of the ride’s structure, which is shaped like a cone with its axis vertical and its sloped sides making an angle of θ = 20.0° with the horizontal as shown in Figure P6.32. This part of the structure rotates about the vertical central axis when the ride operates. The child sits on the sloped surface at a point d = 5.32 m down the sloped side from the center of the cone and pouts. The coefficient of static friction between the boy and the cone is 0.700. The ride operator does not notice that the child has slipped away from his seat and so continues to operate the ride. As a result, the sitting, pouting boy rotates in a circular path at a speed of 3.75 m/s.
Figure P6.32
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A bicycle is turned upside
down while its owner repairs a flat
tire. A friend spins the other wheel
and observes that drops of water
fly off tangentially. She measures
the heights reached by drops mov-
ing vertically (Fig. P7.8). A drop
that breaks loose from the tire on
one turn rises vertically 54.0 cm
above the tangent point. A drop
that breaks loose on the next turn
Figure P7.8
rises 51.0 cm above the tangent
point. The radius of the wheel
is 0.381 m. (a) Why does the first drop rise higher than the
second drop? (b) Neglecting air friction and using only the
observed heights and the radius of the wheel, find the wheel's
angular acceleration (assuming it to be constant).
Problems 8 and 69.
In a home laundry dryer, a cylindrical tub containing wet clothes is rotated steadily about a horizontal axis, as shown in Figure P7.61. So that the clothes will dry uniformly, they are made to tumble. The rate of rotation of the smooth-walled tub is chosen so that a small piece of cloth will lose contact with the tub when the cloth is at an angle of0 = 68.0° above the horizontal. If the radius of the tub is r = 0.330 m, what rate of revolution is needed in revolutions per second?
Answer is 26. Please show me how to obtain it.
Chapter 6 Solutions
Bundle: Physics For Scientists And Engineers With Modern Physics, Loose-leaf Version, 10th + Webassign Printed Access Card For Serway/jewett's Physics For Scientists And Engineers, 10th, Single-term
Ch. 6.1 - You are riding on a Ferris wheel that is rotating...Ch. 6.2 - A bead slides at constant speed along a curved...Ch. 6.3 - Consider the passenger in the car making a left...Ch. 6.4 - A basketball and a 2-inch-diameter steel ball,...Ch. 6 - In the Bohr model of the hydrogen atom, an...Ch. 6 - Whenever two Apollo astronauts were on the surface...Ch. 6 - A car initially traveling eastward turns north by...Ch. 6 - A curve in a road forms part of a horizontal...Ch. 6 - In a cyclotron (one type of particle accelerator),...Ch. 6 - Why is the following situation impossible? The...
Ch. 6 - You are working during your summer break as an...Ch. 6 - Prob. 8PCh. 6 - Prob. 9PCh. 6 - A 40.0-kg child swings in a swing supported by two...Ch. 6 - Prob. 11PCh. 6 - One end of a cord is fixed and a small 0.500-kg...Ch. 6 - A roller coaster at the Six Flags Great America...Ch. 6 - An object of mass m = 5.00 kg, attached to a...Ch. 6 - A person stands on a scale in an elevator. As the...Ch. 6 - Review. A student, along with her backpack on the...Ch. 6 - A small container of water is placed on a...Ch. 6 - The mass of a sports car is 1 200 kg. The shape of...Ch. 6 - Review. A window washer pulls a rubber squeegee...Ch. 6 - A small piece of Styrofoam packing material is...Ch. 6 - Prob. 21PCh. 6 - Assume the resistive force acting on a speed...Ch. 6 - You can feel a force of air drag on your hand if...Ch. 6 - A car travels clockwise at constant speed around a...Ch. 6 - A string under a tension of 50.0 N is used to...Ch. 6 - Disturbed by speeding cars outside his workplace,...Ch. 6 - A car of mass m passes over a hump in a road that...Ch. 6 - A childs toy consists of a small wedge that has an...Ch. 6 - A seaplane of total mass m lands on a lake with...Ch. 6 - An object of mass m1 = 4.00 kg is tied to an...Ch. 6 - A ball of mass m = 0.275 kg swings in a vertical...Ch. 6 - Why is the following situation impossible? A...Ch. 6 - The pilot of an airplane executes a loop-the-loop...Ch. 6 - A basin surrounding a drain has the shape of a...Ch. 6 - Review. While learning to drive, you arc in a 1...Ch. 6 - A truck is moving with constant acceleration a up...Ch. 6 - Prob. 37APCh. 6 - A puck of mass m1 is tied to a string and allowed...Ch. 6 - Prob. 39APCh. 6 - Members of a skydiving club were given the...Ch. 6 - A car rounds a banked curve as discussed in...Ch. 6 - Prob. 42APCh. 6 - Review. A piece of putty is initially located at...Ch. 6 - A model airplane of mass 0.750 kg flies with a...Ch. 6 - A 9.00-kg object starting from rest falls through...Ch. 6 - For t 0, an object of mass m experiences no force...Ch. 6 - A golfer tees off from a location precisely at i =...Ch. 6 - A single bead can slide with negligible friction...Ch. 6 - Prob. 49CPCh. 6 - You have a great job working at a major league...
Additional Science Textbook Solutions
Find more solutions based on key concepts
2. Which of the following is the best example of the use of a referent? _
a. A red bicycle
b. Big as a dump tru...
Physical Science
The Rankine temperature scale (abbreviatedR) uses the same size degrees as Fahrenheit, but measured up from abs...
An Introduction to Thermal Physics
Check Your Understanding If the line spacing of a diffraction grating d is not precisely known, we can use a li...
University Physics Volume 3
1. What are the temperatures for freezing water on the Celsius and the Fahrenheit scales, respectively? For boi...
Conceptual Physical Science (6th Edition)
Given: W = 132 J t = 7.00 s p = ?
Applied Physics (11th Edition)
Choose the best answer to each of the following. Explain your reasoning. Which of these star clusters is oldest...
Cosmic Perspective Fundamentals
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Why is the following situation impossible? A space station shaped like a giant wheel has a radius of r = 100 m and a moment of inertia of 5.00 108 kg m2. A crew of 150 people of average mass 65.0 kg is living on the rim, and the stations rotation causes the crew to experience an apparent free-fall acceleration of g (Fig. P10.52). A research technician is assigned to perform an experiment in which a ball is dropped at the rim of the station every 15 minutes and the time interval for the ball to drop a given distance is measured as a test to make sure the apparent value of g is correctly maintained. One evening, 100 average people move to the center of the station for a union meeting. The research technician, who has already been performing his experiment for an hour before the meeting, is disappointed that he cannot attend the meeting, and his mood sours even further by his boring experiment in which every time interval for the dropped ball is identical for the entire evening.arrow_forwardA variation of the amusement park ride discussed in Problem 11 is the Gravitron, which consists of a rotating cylinder, where riders stand with their backs against the inner surface of the cylinder (see image). As the cylinder rotates faster, riders get stuck to the wall. The effect is great enough, that in some rides, the floor even drops away. Let’s model the Gravitron as a rotating cylinder with vertical walls. The radius of the cylinder is 5.5 m. At one point during the ride, the speed of the Gravitron is 24 rpm, at which point a rider slides down the wall at constant speed. What is the coefficient of kinetic friction between the rider and the wall?arrow_forwardTwo bugs, Buzz and Crunchy, are siting on a spinning disk on a horizontal plane. Buzz is sitting halfway and Crunchy is sitting at the outer edge as shown. The radius of the disk is 0.80 m and the disk is rotating with an angular speed of 38 rpm. The coefficient of friction between the bugs and the disk are us = 0.80 and uk= 0.60. What is Buzz's speed, in m/s? Your answer needs to have 2 significant figures, including the negative sign in your answer if needed. Do not include the positive sign if the answer is positive. No unit is needed in your answer, it is already given in the question statement. Buzz Crunchyarrow_forward
- There is a clever kitchen gadget for drying lettuce leaves after you wash them. It consists of a cylindrical container mounted so that it can be rotated about its axis by turning a hand crank. The outer wall of the cylinder is perforated with small holes. You put the wet leaves in the container and turn the crank to spin off the water. The radius of the container is 15.0 cm. When the cylinder is rotating at 1.64 revolutions per second, what is the magnitude of the centripetal acceleration at the outer wall?arrow_forwardDavid is getting ready to take down the mighty Goliath. David ties a 583 g rock to a rope that is 2.30 m in length. If David starts to swing the rope in a horizontal circle and is tilted down at a 5.94° angle, what is angular speed of the rock?arrow_forwardCasting of molten metal is important in many industrial processes. Centrifugal casting is used for manufacturing pipes, bearings, and many other structures. A cylindrical enclosure is rotated rapidly and steadily about a horizontal axis, as in Figure P7.64. Molten metal is poured into the rotating cylinder and then cooled, forming the finished product. Turning the cylinder at a high rotation rate forces the solidifying metal strongly to the outside. Any bubbles are displaced toward the axis so that unwanted voids will not be present in the casting. Suppose a copper sleeve of inner radius 2.10 cm and outer radius 2.20 cm is to be cast. To eliminate bubbles and give high structural integrity, the centripetal acceleration of each bit of metal should be 100g What rate of rotation is required? State the answer in revolutions per minute.arrow_forward
- Two bugs, Buzz and Crunchy, are siting on a spinning disk on a horizontal plane. Buzz is sitting halfway and Crunchy is sitting at the outer edge as shown. The radius of the disk is 0.80 m and the disk is rotating with an angular speed of 38 rpm. The coefficient of friction between the bugs and the disk are μs = 0.80 and μk= 0.60. What is Crunchy's speed, in m/s?arrow_forwardA common carnival ride, called a gravitron, is a large cylinder in which people stand against the wall of the ride as it rotates. At a certain point the floor of the cylinder lowers and the people are surprised that they don't slide down. Suppose the radius of the cylinder is r = 12 m, and the friction between the wall and their clothes is μ = 0.62. Consider the tangential speed v of the ride's occupants as the cylinder spins. a) What is the minimum speed, in meters per second, that the cylinder must make a person move at to ensure they will "stick" to the wall? Vmin = b) What is the frequency fin revolutions per minute of the carnival ride when it has reached the minimum speed to "stick" someone to the wall? f=arrow_forwardThe grand jeté is a classic ballet maneuver in which a dancer executes a horizontal leap while moving her arms and legs up and then down. At the center of the leap, the arms and legs are gracefully extended, as we see in P7.81a. The goal of the leap is to create the illusion of flight. As the dancer moves through the air, he or she is in free fall. But what part of the dancer follows the usual parabolic path? It won’t come as a surprise to learn that it’s the center of gravity. But when you watch a dancer leap through the air, you don’t watch her center of gravity, you watch her head. If the translational motion of her head is horizontal—not parabolic—this creates the illusion that she is flying through the air, held up by unseen forces.P7.81b illustrates how the dancer creates this illusion. While in the air, she changes the position of her center of gravity relative to her body by moving her arms and legs up, then down. Her center of gravity moves in a parabolic path, but her head…arrow_forward
- The grand jeté is a classic ballet maneuver in which a dancer executes a horizontal leap while moving her arms and legs up and then down. At the center of the leap, the arms and legs are gracefully extended, as we see in P7.81a. The goal of the leap is to create the illusion of flight. As the dancer moves through the air, he or she is in free fall. But what part of the dancer follows the usual parabolic path? It won’t come as a surprise to learn that it’s the center of gravity. But when you watch a dancer leap through the air, you don’t watch her center of gravity, you watch her head. If the translational motion of her head is horizontal—not parabolic—this creates the illusion that she is flying through the air, held up by unseen forces.P7.81b illustrates how the dancer creates this illusion. While in the air, she changes the position of her center of gravity relative to her body by moving her arms and legs up, then down. Her center of gravity moves in a parabolic path, but her head…arrow_forwardThe grand jeté is a classic ballet maneuver in which a dancer executes a horizontal leap while moving her arms and legs up and then down. At the center of the leap, the arms and legs are gracefully extended, as we see in P7.81a. The goal of the leap is to create the illusion of flight. As the dancer moves through the air, he or she is in free fall. But what part of the dancer follows the usual parabolic path? It won’t come as a surprise to learn that it’s the center of gravity. But when you watch a dancer leap through the air, you don’t watch her center of gravity, you watch her head. If the translational motion of her head is horizontal—not parabolic—this creates the illusion that she is flying through the air, held up by unseen forces.P7.81b illustrates how the dancer creates this illusion. While in the air, she changes the position of her center of gravity relative to her body by moving her arms and legs up, then down. Her center of gravity moves in a parabolic path, but her head…arrow_forwardThe grand jeté is a classic ballet maneuver in which a dancer executes a horizontal leap while moving her arms and legs up and then down. At the center of the leap, the arms and legs are gracefully extended, as we see in P7.81a. The goal of the leap is to create the illusion of flight. As the dancer moves through the air, he or she is in free fall. But what part of the dancer follows the usual parabolic path? It won’t come as a surprise to learn that it’s the center of gravity. But when you watch a dancer leap through the air, you don’t watch her center of gravity, you watch her head. If the translational motion of her head is horizontal—not parabolic—this creates the illusion that she is flying through the air, held up by unseen forces.P7.81b illustrates how the dancer creates this illusion. While in the air, she changes the position of her center of gravity relative to her body by moving her arms and legs up, then down. Her center of gravity moves in a parabolic path, but her head…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Moment of Inertia; Author: Physics with Professor Matt Anderson;https://www.youtube.com/watch?v=ZrGhUTeIlWs;License: Standard Youtube License