Chapter 6, Problem 48CP

A single bead can slide with negligible friction on a stiff wire that has been bent into a circular loop of radius 15.0 cm as shown in Figure P6.48. The circle is always in a vertical plane and rotates steadily about its vertical diameter with a period of 0.450 s. The position of the bead is described by the angle θ that the radial line, from the center of the loop to the bead, makes with the vertical. (a) At what angle up from the bottom of the circle can the bead slay motionless relative to the turning circle? (b) What If? Repeat the problem, this time taking the period of the circle’s rotation as 0.850 s. (c) Describe how the solution to part (b) is different from the solution to part (a). (d) For any period or loop size, is there always an angle at which the bead can stand still relative to the loop? (e) Are there ever more than two angles? Arnold Arons suggested the idea for this problem.

Figure P6.48

To determine

The angle from the bottom of the circle for which the bead can stay motionless.

Answer to Problem 48CP

The angles from the bottom of the circle for which the bead can stay motionless are $0.0°$ and $70.4°$.

Explanation of Solution

Given info: The radius of the circular loop is $15.0\text{cm}$, the period of the rotation is $0.450\text{s}$, the angle between the vertical and the radial line from the centre of the loop.

The acceleration due to gravity is $9.8{\text{m}/\text{s}}^2$.

The rough sketch of the force body diagram of the situation is shown below,

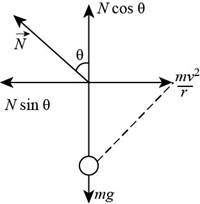
Figure (1)

The bead moves in a circle,

$r=R\sin \theta$

Here,

$R$ is the radius of the hoop.

$r$ is the radius of the circle in which the bead moves.

$\theta$ is the angle between the vertical and the radial line from the centre of the loop.

The speed of the bead is,

$v=\frac{2\pi r}{T}$

Here,

$T$ is the time period of the rotation.

From the figure (1) the net force in $y$ direction is,

$\begin{array}{c}N\cos \theta -mg=0\\ N=\frac{mg}{\cos \theta }\end{array}$

Here,

$N$ is the normal force acting on the bead.

$m$ is the amass of the bead.

$g$ is the acceleration due to gravity.

The net force in $x$ direction is,

$N\sin \theta =m\frac{v^2}{r}$

Substitute $\frac{2\pi r}{T}$ for $v$ in the above equation.

$N\sin \theta =m\left[\frac{{\left(\frac{2\pi r}{T}\right)}^2}{r}\right]$

Substitute $R\sin \theta$ for $r$ and $\frac{mg}{\cos \theta }$ for $N$ in the above equation.

$\begin{array}{c}\frac{mg}{\cos \theta }\sin \theta =m\left[\frac{{\left(\frac{2\pi R\sin \theta }{T}\right)}^2}{R\sin \theta }\right]\\ g\frac{\sin \theta }{\cos \theta }-\frac{4{\pi }^{2}R\sin \theta }{T^2}=0\\ \sin \theta \left(\frac{g}{\cos \theta }-\frac{4{\pi }^{2}R}{T^2}\right)=0\end{array}$ . (1)

The two possible solutions are,

$\begin{array}{c}\sin \theta =0\\ \theta =0°\end{array}$

and,

$\begin{array}{c}\frac{g}{\cos \theta }-\frac{4{\pi }^{2}R}{T^2}=0\\ \frac{g}{\cos \theta }=\frac{4{\pi }^{2}R}{T^2}\\ \cos \theta =\frac{g{T}^2}{4{\pi }^{2}R}\end{array}$

Substitute $15.0\text{cm}$ for $R$, $0.450\text{s}$ and $9.8{\text{m}/\text{s}}^2$ for $g$ in the above equation.

$\begin{array}{c}\cos \theta =\frac{\left(9.8{\text{m}/\text{s}}^2\right){\left(0.450\text{ s}\right)}^2}{4{\pi }^2\left(15\text{cm}\times \frac{\text{1}\text{m}}{100\text{cm}}\right)}\\ =0.335\\ \theta ={\text{cos}}^{\text{-1}}\left(0.335\right)\\ =70.42°\end{array}$

Conclusion:

Therefore, the angles from the bottom of the circle for which the bead can stay motionless are $0.0°$ and $70.4°$.

To determine

The angles from the bottom of the circle for which the bead can stay motionless for the time period as $0.850\text{s}$.

Answer to Problem 48CP

The only one possible angle from the bottom of the circle for which the bead can stay motionless for time period $0.850\text{s}$ is $0.0°$.

Explanation of Solution

Given info: The radius of the circular loop is $15.0\text{cm}$, the period of the rotation is $0.450\text{s}$, the angle between the vertical and the radial line from the centre of the loop.

The acceleration due to gravity is $9.8{\text{m}/\text{s}}^2$.

Form the part (a) equation (1).

$\sin \theta \left(\frac{g}{\cos \theta }-\frac{4{\pi }^{2}R}{T^2}\right)=0$

The possible solutions are,

$\begin{array}{c}\sin \theta =0\\ \theta =0°\end{array}$

and,

$\begin{array}{l}\frac{g}{\cos \theta }=\frac{4{\pi }^{2}R}{T^2}\\ \cos \theta =\frac{g{T}^2}{4{\pi }^{2}R}\end{array}$

Substitute $15.0\text{cm}$ for $R$, $0.850\text{s}$ and $9.8{\text{m}/\text{s}}^2$ for $g$ in the above equation.

$\begin{array}{c}\cos \theta =\frac{\left(9.8{\text{m}/\text{s}}^2\right){\left(0.850\text{ s}\right)}^2}{4{\pi }^2\left(15\text{cm}\times \frac{\text{1}\text{m}}{100\text{cm}}\right)}\\ =1.19\\ \theta ={\cos }^{-1}\left(1.19\right)\end{array}$

The above value is not possible.

Conclusion:

Therefore, the only one possible angle from the bottom of the circle for which the bead can stay motionless at time period $0.850\text{s}$ is $0.0°$.

To determine

The difference between the solution of the part (a) and part (b).

Answer to Problem 48CP

The part (b) has only one solution as the time period is very large.

Explanation of Solution

Given info: The radius of the circular loop is $15.0\text{cm}$, the period of the rotation is $0.450\text{s}$, the angle between the vertical and the radial line from the centre of the loop.

Form equation (1)

$\sin \theta \left(\frac{g}{\cos \theta }-\frac{4{\pi }^{2}R}{T^2}\right)=0$

The possible solutions are,

$\begin{array}{c}\sin \theta =0\\ \theta =0°\end{array}$

and,

$\begin{array}{c}\frac{g}{\cos \theta }=\frac{4{\pi }^{2}R}{T^2}\\ \cos \theta =\frac{g{T}^2}{4{\pi }^{2}R}\\ \cos \theta \propto T^2\end{array}$

As the second solution depends directly on the square of the amplitude of the time period so, as the time period increases the value of $\cos \theta$ increases to value greater than $1$ which is not possible as the range of the cosine function is $-1\le \cos \theta \le +1$.

Conclusion:

Therefore, the part (b) has only one solution as the time period is very large.

To determine

The angle at which the bead can stand still relative to the loop.

Answer to Problem 48CP

The angle for which condition $g{T}^2<4{\pi }^{2}R$ and $\theta =0°$ is followed the angles are possible for the beads to stand still.

Explanation of Solution

Given info: The radius of the circular loop is $15.0\text{cm}$, the period of the rotation is $0.450\text{s}$, the angle between the vertical and the radial line from the centre of the loop.

Form equation (1)

$\sin \theta \left(\frac{g}{\cos \theta }-\frac{4{\pi }^{2}R}{T^2}\right)=0$

The possible solutions are,

$\begin{array}{c}\sin \theta =0\\ \theta =0°\end{array}$

and,

$\begin{array}{c}\frac{g}{\cos \theta }=\frac{4{\pi }^{2}R}{T^2}\\ \cos \theta =\frac{g{T}^2}{4{\pi }^{2}R}\end{array}$

As the range of the cosine function is $-1\le \cos \theta \le +1$, the solution to occur the condition is to be followed is,

$\begin{array}{c}\frac{g{T}^2}{4{\pi }^{2}R}<1\\ g{T}^2<4{\pi }^{2}R\end{array}$

So, the value of the cosine of the angle is always less than $1$.

Conclusion:

Therefore, for the condition $g{T}^2<4{\pi }^{2}R$ and $\theta =0°$ the angles are possible for the beads to stand still.

To determine

Whether there are more than two angles.

Answer to Problem 48CP

The number of possible angles are $2$ for a given time period.

Explanation of Solution

Given info: The radius of the circular loop is $15.0\text{cm}$, the period of the rotation is $0.450\text{s}$, the angle between the vertical and the radial line from the centre of the loop.

Form equation (1)

$\sin \theta \left(\frac{g}{\cos \theta }-\frac{4{\pi }^{2}R}{T^2}\right)=0$

The possible solutions are,

$\begin{array}{c}\sin \theta =0\\ \theta =0°\end{array}$

and,

$\begin{array}{c}\frac{g}{\cos \theta }=\frac{4{\pi }^{2}R}{T^2}\\ \cos \theta =\frac{g{T}^2}{4{\pi }^{2}R}\end{array}$

Form the above expression the second solution depends on time period, acceleration due to gravity and the radius of the hoop and for a given case the parameters has only one value so the second solution has only one answer.

Conclusion:

Therefore, the number of possible angles are $2$ for a given time period.