
Concept explainers
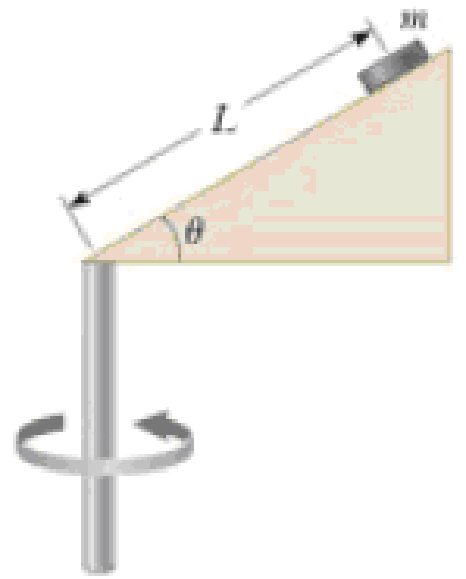
A child’s toy consists of a small wedge that has an acute angle θ (Fig. P6.28). The sloping side of the wedge is frictionless, and an object of mass m on it remains at constant height if the wedge is spun at a certain constant speed. The wedge is spun by rotating, as an axis, a vertical rod that is firmly attached to the wedge at the bottom end. Show that, when the object sits at rest at a point at distance L up along the wedge, the speed of the object must be v = (gL sin θ)1/2.
Figure P6.28
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
Bundle: Physics For Scientists And Engineers With Modern Physics, Loose-leaf Version, 10th + Webassign Printed Access Card For Serway/jewett's Physics For Scientists And Engineers, 10th, Single-term
Additional Science Textbook Solutions
College Physics: A Strategic Approach (3rd Edition)
Fundamentals Of Thermodynamics
Organic Chemistry
Cosmic Perspective Fundamentals
Chemistry: A Molecular Approach (4th Edition)
Biology: Life on Earth with Physiology (11th Edition)
- ་ The position of a particle is described by r = (300e 0.5t) mm and 0 = (0.3t²) rad, where t is in seconds. Part A Determine the magnitude of the particle's velocity at the instant t = 1.5 s. Express your answer to three significant figures and include the appropriate units. v = Value Submit Request Answer Part B ? Units Determine the magnitude of the particle's acceleration at the instant t = 1.5 s. Express your answer to three significant figures and include the appropriate units. a = Value A ? Unitsarrow_forwardSolve and answer the question correctly please. Thank you!!arrow_forwardSolve and answer the question correctly please. Thank you!!arrow_forward
- A spiral transition curve is used on railroads to connect a straight portion of the track with a curved portion. (Figure 1) Part A v = v₁ft/s 600 ft y = (106) x³ If the spiral is defined by the equation y = (106)³, where x and y are in feet, determine the magnitude of the acceleration of a train engine moving with a constant speed of v₁ = 30 ft/s when it is at point x = 600 ft. Express your answer to three significant figures and include the appropriate units. ? a = Value Unitsarrow_forwardsolve and answer the problem correctly please. Thank you!!arrow_forwardSolve and answer the question correctly please. Thank you!!arrow_forward
- Solve and answer the question correctly please. Thank you!!arrow_forwardWhen the motorcyclist is at A, he increases his speed along the vertical circular path at the rate of = (0.3t) ft/s², where t is in seconds. Take p = 360 ft. (Figure 1) Part A 60° Ρ B If he starts from rest at A, determine the magnitude of his velocity when he reaches B. Express your answer to three significant figures and include the appropriate units. v = Value Submit Request Answer ་ Part B ? Units If he starts from rest at A, determine the magnitude of his acceleration when he reaches B. Express your answer to three significant figures and include the appropriate units. 11 ? a = Value Unitsarrow_forwardThe car starts from rest at s = 0 and increases its speed at a₁ = 7 m/s². (Figure 1) Part A = 40 m Determine the time when the magnitude of acceleration becomes 20 m/s². Express your answer to three significant figures and include the appropriate units. ? t = Value Units Part B At what position s does this occur? Express your answer to three significant figures and include the appropriate units. s = Value Submit Request Answer ? Unitsarrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





