
The tip of a one-link robot is located at
FIGURE P6.1 Rotating one-link robot starting at
To plot:
The
Answer to Problem 1P
The graph for
The graph for
The amplitude of sine and cosine function is
Explanation of Solution
Given:
The tip of a one-link robot is initially located at

Time taken for the robot to move form
A one-link robot is length of
Concept used:
Write the expression for the linear frequency.
Here,
Write the expression for the angular frequency.
Here,
Write the expression for the time period.
Write the expression for
Here,
Write the expression for
Here,
Write the expression for the time shift.
Here,
Calculation:
The one-link robot completes one revolution in
Substitute
Substitute
Therefore, the period of the tip of a one-link robot is
Substitute
Therefore, the frequency is
Since the one-link robot initially start form
Substitute
Here,
Substitute
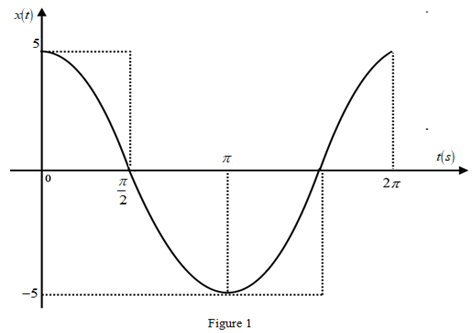
The plot for the
Substitute
Substitute
The plot for the
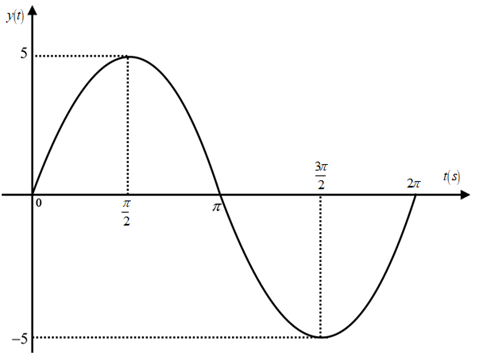
Figure 2
Substitute
Therefore, the time shift of the one-link robot is
The amplitude of sine and cosine function is
Conclusion:
Thus, the graph for
Want to see more full solutions like this?
Chapter 6 Solutions
Introductory Mathematics for Engineering Applications
Additional Math Textbook Solutions
Elementary Statistics: Picturing the World (7th Edition)
Calculus: Early Transcendentals (2nd Edition)
Elementary Statistics (13th Edition)
Introductory Statistics
Elementary Statistics
Thinking Mathematically (6th Edition)
- Solve the given symbolic initial value problem and sketch a graph of the solution. y"+y=38 (1-2); y(0) = 0, y'(0) = 2arrow_forwardB\ Prove that if T is a spanning tree of G which contains e, then Te Is a spanning tree of G * e.arrow_forward9 Q/ Let G be agraph with n vertices, then G has at least two vertices which are not cut vertices.arrow_forward
- Find the first four nonzero terms in a power series expansion about x=0 for a general solution to the given differential equation w''-14x^2w'+w=0arrow_forwardIn this exercise, we will investigate a technique to prove that a language is notregular. This tool is called the pumping lemma.The pumping lemma says that if M = (S, I, f, s0, F ) is a DFA with p states (i.e., p = |S|) and if the wordw is in L(M ) (the language generated by M ) and w has length greater than or equal to p, then w may bedivided into three pieces, w = xyz, satisfying the following conditions:1. For each i ∈ N, xy^i z ∈ L(M ).2. |y| > 0 (i.e., y contains at least one character).3. |xy| ≤ p (i.e., the string xy has at most p characters). Use the pumping lemma to show the following language is not regular (HINT: Use proof by contradictionto assume the language is regular and apply the pumping lemma to the language):L = {0^k1^k | k ∈ N}arrow_forwardA prefix of length ℓ of some word w are the first ℓ characters (in order) of w.1. Construct a context-free grammar for the language: L = {w ∈ {a, b}∗ | every prefix of w has at least as many a’s as b’s}2. Explain why every word generated by your context-free grammar (in Part 1) is contained in L. Then,prove via induction that every w ∈ L is produced by your context-free grammar.arrow_forward
- Consider a simplified version of American football where on any possession ateam can earn 0, 3 or 7 points. What is the smallest number n0 of points such that for all n ≥ n0 and n ∈ Na team could earn n points. You must prove that your answer is correct via induction (HINT: Don’t forgetto show that n0 is the smallest number above which any number of points is reachable).arrow_forwardConsider a vocabulary consisting of the nucleotide bases V = {A, T, G, C}.Construct a DFA to recognize strings which end in AAGT .(a) Draw the DFA with clear markings of all states including start and acceptance state(s).(b) Simulate the DFA to show that string T GAAGT will be accepted by the DFA.(c) Simulate the DFA to show that string T AAGT G will not be accepted by the DFA.arrow_forwardA palindrome is a string that reads the same backward as it does forward. For example, abaaaba is a palindrome. Suppose that we need to define a language that generates palindromes.(a) Define a phase structure grammar that generates the set of all palindromes over the alphabet {a, b}clearly describing the recursive rules that generates palindromes. Use the notation Symbol → rule. Theempty set is denoted by λ. Clearly identify the terminal and non-terminal symbols in your grammar.(b) Show that the palindrome abaaaba can be recognized by your grammar. To show this, show all stepsof parsing the expression abaaaba using the rules you defined above.arrow_forward
- A full k-ary tree is a (rooted) tree whose nodes either have exactly k children (internal nodes) or have no children (leaves). Using structural induction, formally prove that every full k-ary tree that has x internal nodes has exactly kx + 1 nodes in total. Note that for full binary trees, i.e., when k = 2, this would imply that the total number of nodes is 2x + 1.arrow_forwardW AutoSave Off Soal Latihan Matdis (1) ▼ Search File Home Insert Draw Design Layout References Mailings Review View Help Aptos (Body) ✓ 12 A A Aa Ро Paste BI U ab x, x² A ✓ A ད Clipboard ₪ 24 23 22 21 20 19 18 17 16 15 1″ ידידיו Page 1 of 1 25°C 215 words Berawan E> M Font 四 Paragraph 3 4 1 56 ☑ 781 LI Comments Editing Find ✓ Normal No Spacing Heading Replace Add-ins Select Styles ☑ Editing Add-ins 91 10 111 12 | 13| 14 15 5. Suppose you wanted to draw a quadrilateral using the dots below as vertices (corners). The dots are spaced one unit apart horizontally and two units apart vertically. a) How many quadrilaterals are possible? b) How many are squares? How many are rectangles? c) How many are parallelograms? English (Indonesia) Accessibility: Investigate R - W ☑ Share ▾ Focus + 100% 00:17 13/04/2025arrow_forward2. Show that 8 xa S -dx (b² + 12) dr = 2 cos(π2) пра-1 a, b real and -1 0 Your solution should clearly explain the closed contour you are using, and state clearly any vanishing properties of integrals over contours that are being used. You are free to quote from the lectures, the appropriate results on such vanishing properties, without deriving these properties. Any residue calculations involved should be explained clearly.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
