
Practice Problem 5.5 (solution page 575)
Suppose we wish to write a function to evaluate I polynomial where a polynomial of degree n is defined to have a set of coefficients a0, a1 a2 ….an. For a value x. we evaluate the polynomial by computing
(5.2) a() + a1x + a2x2 + + anxn (5.2)
This evaluation can be implemented by the following function, having as arguments an array of coefficients a, a value x, and the polynomial degree degree (the value n in Equation 5.2). In this function, we compute both the successive terms of the equation and the successive powers of x within a single loop:
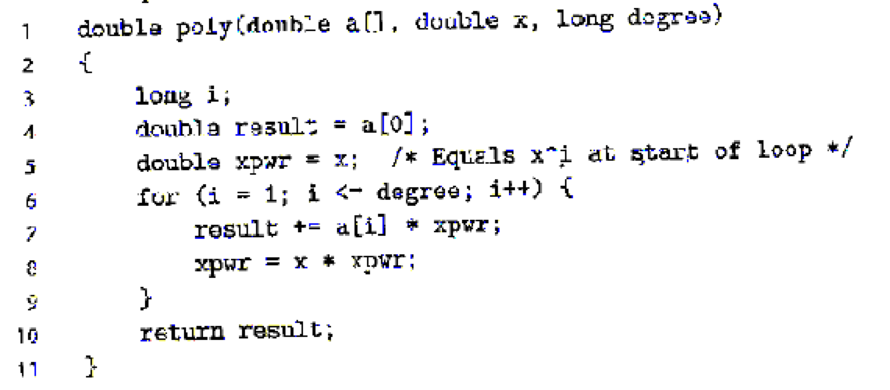
- A. For degree n, how many additions and how many multiplications does this code perform?
- B. On our reference machine, with arithmetic operations having the latencies shown in Figure 5.12, we measure the CPE for this function to be 5.00. Explain how this CPE arises based on the data dependencies formed between iterations due to the operations implementing lines 7-8 of the function.
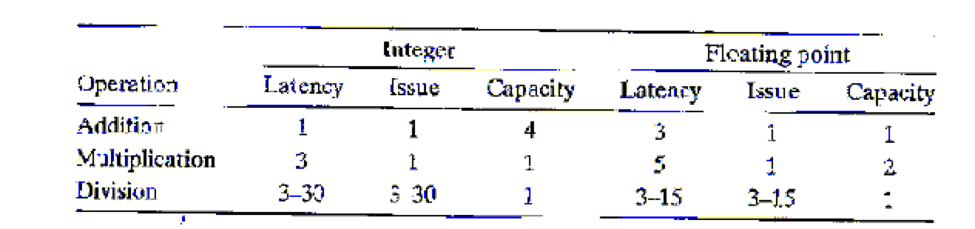
Figure 5.12 Latency, issue time, and capacity characteristics of reference machine operations. Latency indicates the total number of clock cycles required to perform the actual operations, while issue time indicates the minimum number of cycles between two independent operations. The capacity indicates how many of these operations can be issued simultaneously. The times for division depend on the data values.
Want to see the full answer?
Check out a sample textbook solution
Chapter 5 Solutions
Computer Systems: A Programmer's Perspective (3rd Edition)
Additional Engineering Textbook Solutions
Elementary Surveying: An Introduction To Geomatics (15th Edition)
Starting Out with Java: From Control Structures through Data Structures (4th Edition) (What's New in Computer Science)
Java How to Program, Early Objects (11th Edition) (Deitel: How to Program)
Electric Circuits. (11th Edition)
Mechanics of Materials (10th Edition)
Java: An Introduction to Problem Solving and Programming (8th Edition)
- Need help with coding in this in python!arrow_forwardIn the diagram, there is a green arrow pointing from Input C (complete data) to Transformer Encoder S_B, which I don’t understand. The teacher model is trained on full data, but S_B should instead receive missing data—this arrow should not point there. Please verify and recreate the diagram to fix this issue. Additionally, the newly created diagram should meet the same clarity standards as the second diagram (Proposed MSCATN). Finally provide the output image of the diagram in image format .arrow_forwardPlease provide me with the output image of both of them . below are the diagrams code make sure to update the code and mentionned clearly each section also the digram should be clearly describe like in the attached image. please do not provide the same answer like in other question . I repost this question because it does not satisfy the requirment I need in terms of clarifty the output of both code are not very well details I have two diagram : first diagram code graph LR subgraph Teacher Model (Pretrained) Input_Teacher[Input C (Complete Data)] --> Teacher_Encoder[Transformer Encoder T] Teacher_Encoder --> Teacher_Prediction[Teacher Prediction y_T] Teacher_Encoder --> Teacher_Features[Internal Features F_T] end subgraph Student_A_Model[Student Model A (Handles Missing Values)] Input_Student_A[Input M (Data with Missing Values)] --> Student_A_Encoder[Transformer Encoder E_A] Student_A_Encoder --> Student_A_Prediction[Student A Prediction y_A] Student_A_Encoder…arrow_forward
- Why I need ?arrow_forwardHere are two diagrams. Make them very explicit, similar to Example Diagram 3 (the Architecture of MSCTNN). graph LR subgraph Teacher_Model_B [Teacher Model (Pretrained)] Input_Teacher_B[Input C (Complete Data)] --> Teacher_Encoder_B[Transformer Encoder T] Teacher_Encoder_B --> Teacher_Prediction_B[Teacher Prediction y_T] Teacher_Encoder_B --> Teacher_Features_B[Internal Features F_T] end subgraph Student_B_Model [Student Model B (Handles Missing Labels)] Input_Student_B[Input C (Complete Data)] --> Student_B_Encoder[Transformer Encoder E_B] Student_B_Encoder --> Student_B_Prediction[Student B Prediction y_B] end subgraph Knowledge_Distillation_B [Knowledge Distillation (Student B)] Teacher_Prediction_B -- Logits Distillation Loss (L_logits_B) --> Total_Loss_B Teacher_Features_B -- Feature Alignment Loss (L_feature_B) --> Total_Loss_B Partial_Labels_B[Partial Labels y_p] -- Prediction Loss (L_pred_B) --> Total_Loss_B Total_Loss_B -- Backpropagation -->…arrow_forwardPlease provide me with the output image of both of them . below are the diagrams code I have two diagram : first diagram code graph LR subgraph Teacher Model (Pretrained) Input_Teacher[Input C (Complete Data)] --> Teacher_Encoder[Transformer Encoder T] Teacher_Encoder --> Teacher_Prediction[Teacher Prediction y_T] Teacher_Encoder --> Teacher_Features[Internal Features F_T] end subgraph Student_A_Model[Student Model A (Handles Missing Values)] Input_Student_A[Input M (Data with Missing Values)] --> Student_A_Encoder[Transformer Encoder E_A] Student_A_Encoder --> Student_A_Prediction[Student A Prediction y_A] Student_A_Encoder --> Student_A_Features[Student A Features F_A] end subgraph Knowledge_Distillation_A [Knowledge Distillation (Student A)] Teacher_Prediction -- Logits Distillation Loss (L_logits_A) --> Total_Loss_A Teacher_Features -- Feature Alignment Loss (L_feature_A) --> Total_Loss_A Ground_Truth_A[Ground Truth y_gt] -- Prediction Loss (L_pred_A)…arrow_forward
 C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr
C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole
Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole- COMPREHENSIVE MICROSOFT OFFICE 365 EXCEComputer ScienceISBN:9780357392676Author:FREUND, StevenPublisher:CENGAGE L



