Calculus Volume 3
1st Edition
ISBN: 9781630182038
Author: Gilbert Strang, Edwin Jed Herman
Publisher: OpenStax College.
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5.6, Problem 298E
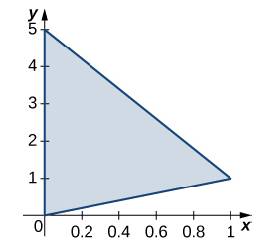
In the following exercises, the region R occupied by a lamina is shown in a graph. Find the mass of R with the density function
298. R is the triangular region with vertices (0, 0), (1, 1), (0, 5); p(x. y)= x+y.
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
show that v3 = (−√3, −3, 3)⊤ is an eigenvector of M3 . Also here find the correspondingeigenvalue λ3 . Just from looking at M3 and its components, can you say something about the remaining twoeigenvalues? If so, what would you say?
find v42 so that v4 = ( 2/5, v42, 1)⊤ is an eigenvector of M4 with corresp. eigenvalue λ4 = 45
2) Suppose we select two values x and y independently from the uniform distribution on
[0,1]. What is the probability that xy
No chatgpt pls will upvote Already got wrong chatgpt answer
Chapter 5 Solutions
Calculus Volume 3
Ch. 5.1 - In the following exercises, use the midpoint rule...Ch. 5.1 - In the following exercises, use the midpoint rule...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...
Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - function over the given rectangles. 35....Ch. 5.1 - function over the given rectangles. 36....Ch. 5.1 - function over the given rectangles. 37....Ch. 5.1 - function over the given rectangles. 38....Ch. 5.1 - Let f and g be two continuous functions such that...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - Let f and g be two continuous functions such that...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, the function f is...Ch. 5.1 - In the following exercises, the function f is...Ch. 5.1 - In the following exercises, the function f is...Ch. 5.1 - In the following exercises, the function f is...Ch. 5.1 - [T] Consider the function f(x,y)=ex2y2where...Ch. 5.1 - [T] Consider the function f(x,y)=sin(x2)cos(y2) ....Ch. 5.1 - In the following exercises, the functions fnare...Ch. 5.1 - In the following exercises, the functions fnare...Ch. 5.1 - In the following exercises, the functions fnare...Ch. 5.1 - In the following exercises, the functions fnare...Ch. 5.1 - An isotherm map is a chart connecting points...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - wIn the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - Evaluate the iterated integrals. 80. 012x3x(x+ y...Ch. 5.2 - Evaluate the iterated integrals. 81....Ch. 5.2 - Evaluate the iterated integrals. 82....Ch. 5.2 - Evaluate the iterated integrals. 83....Ch. 5.2 - Evaluate the iterated integrals. 84. 01 1 y 2 1 y...Ch. 5.2 - Evaluate the iterated integrals. 85. 01/2 14 y 2...Ch. 5.2 - Evaluate the iterated integrals. 86. Let D be the...Ch. 5.2 - Evaluate the iterated integrals. 87. Let D be the...Ch. 5.2 - yEvaluate the iterated integrals. 88. a. Show that...Ch. 5.2 - Evaluate the iterated integrals. 89. a. Show that...Ch. 5.2 - The region D bounded by x=0,y=x5+1 , and S y=3x2...Ch. 5.2 - The legion D bounded by y = cos x. y = 4 cos x....Ch. 5.2 - Find the area A(D) of the region...Ch. 5.2 - Let D be the region bounded by y = 1, y = x. y =...Ch. 5.2 - Find the average value of the function f(x. y) =...Ch. 5.2 - Find the average value of the function f(x. y) =-x...Ch. 5.2 - In the following exercises, change the order of...Ch. 5.2 - In the following exercises, change the order of...Ch. 5.2 - In the following exercises, change the order of...Ch. 5.2 - In the following exercises, change the order of...Ch. 5.2 - The region D is shown in the following figure....Ch. 5.2 - The region D is given in the following figure....Ch. 5.2 - Find the volume of the solid under the surface...Ch. 5.2 - Find the volume of the solid tinder the plane...Ch. 5.2 - Find the volume of the solid tinder the plane z=xy...Ch. 5.2 - Find the volume of the solid under the surface z =...Ch. 5.2 - Let g be a positive, increasing, and...Ch. 5.2 - Let g be a positive, increasing, and...Ch. 5.2 - Find the volume of the solid situated in the first...Ch. 5.2 - Find the volume of the solid situated in the first...Ch. 5.2 - Find the volume of the solid bounded by the planes...Ch. 5.2 - Find the volume of the solid bounded by the planes...Ch. 5.2 - Let S1 and S2 , be the solids situated in the...Ch. 5.2 - Let S and 5, be the solids situated in the first...Ch. 5.2 - Let S1 and S2 be the solids situated in the first...Ch. 5.2 - Let S1 and S2 be the solids situated in the first...Ch. 5.2 - [T] The following figure shows the region D...Ch. 5.2 - [T] The region D bounded by the curves y=cosx,x=0...Ch. 5.2 - Suppose that (X. Y) is the outcome of an...Ch. 5.2 - Consider X and Y two random variables of...Ch. 5.2 - [T] The Reuleaux triangle consists of an...Ch. 5.2 - [T] Show that the area of the lunes of Alhazen,...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, the integrals have...Ch. 5.3 - In the following exercises, the integrals have...Ch. 5.3 - In the following exercises, the integrals have...Ch. 5.3 - In the following exercises, the integrals have...Ch. 5.3 - In the following exercises, convert the integrals...Ch. 5.3 - In the following exercises, convert the integrals...Ch. 5.3 - In the following exercises, convert the integrals...Ch. 5.3 - In the following exercises, convert the integrals...Ch. 5.3 - Evaluate the integral DffrdAwhere D is the region...Ch. 5.3 - Find the area of the region D bounded by the polar...Ch. 5.3 - Evaluate the integral DrdA, where D is the region...Ch. 5.3 - Find the total area of the region enclosed by the...Ch. 5.3 - Find the area of the region D, which is the region...Ch. 5.3 - Find the area of the region D. which is the region...Ch. 5.3 - Determine the average value of the function f(x....Ch. 5.3 - Determine the average value of the function...Ch. 5.3 - Find the volume of the solid situated in the first...Ch. 5.3 - Find the volume of the solid bounded by the...Ch. 5.3 - a. Find the volume of the solid S1 bounded by the...Ch. 5.3 - a. Find the volume of the solid S1 inside the unit...Ch. 5.3 - For the following two exercises, consider a...Ch. 5.3 - For the following two exercises, consider a...Ch. 5.3 - Find the volume of the solid that lies tinder the...Ch. 5.3 - Find the volume of the solid that lies under the...Ch. 5.3 - Find the volume of the solid that lies under the...Ch. 5.3 - Find the volume of the solid that lies under the...Ch. 5.3 - A radial function f is a function whose value at...Ch. 5.3 - Use the information from the preceding exercise to...Ch. 5.3 - Let f(x,y)=F(r)rbe a continuous radial function...Ch. 5.3 - Apply the preceding exercise to calculate the...Ch. 5.3 - Let f be a continuous function that can be...Ch. 5.3 - Apply the preceding exercise to calculate the...Ch. 5.3 - Let f be a continuous function that can be...Ch. 5.3 - Evaluate Dff arctan (yx)x2+y2dA. where...Ch. 5.3 - A spherical cap is the region of a sphere that...Ch. 5.3 - In statistics, the joint density for two...Ch. 5.3 - The double improper integral e( x2 +y 2/2 )dxdymay...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, change the order of...Ch. 5.4 - In the following exercises, change the order of...Ch. 5.4 - In the following exercises, change the order of...Ch. 5.4 - In the following exercises, change the order of...Ch. 5.4 - Let F. G and H be continuous functions on [a,b]...Ch. 5.4 - Let F. G. and H be differential functions on...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - The solid E bounded by y2+z2=9,x=0 . x = 5 is...Ch. 5.4 - The solid E bounded by y=x,x=4,y=0 , and z = 1 is...Ch. 5.4 - [T] The volume of a solid E is given by the...Ch. 5.4 - [T] The volume of a solid E is given by the...Ch. 5.4 - In the following exercises, use two circular...Ch. 5.4 - In the following exercises, use two circular...Ch. 5.4 - In the following exercises, use two circular...Ch. 5.4 - In the following exercises, use two circular...Ch. 5.4 - Set up the integral that gives the volume of the...Ch. 5.4 - Set up the integral that gives the volume of the...Ch. 5.4 - Find the average value of the function f(x. y, z)...Ch. 5.4 - Find the average value of the function...Ch. 5.4 - Find the volume of the solid E that lies under the...Ch. 5.4 - Find the volume of the solid E that lies under the...Ch. 5.4 - Consider the pyramid with the base in the xv...Ch. 5.4 - Consider the pyramid with the base in the xy...Ch. 5.4 - The solid E bounded by the sphere of equation...Ch. 5.4 - The solid E bounded by the equation 9x2+4y2+z2=1...Ch. 5.4 - Find the volume of the prism with vertices (0, 0....Ch. 5.4 - Find the volume of the prism with vertices (0. 0....Ch. 5.4 - The solid E bounded by z= 10—2x—y and situated in...Ch. 5.4 - The solid E bounded by z=1x2 and situated in the...Ch. 5.4 - The midpoint rule for the triple integral...Ch. 5.4 - [T] a. Apply the midpoint rule to approximate...Ch. 5.4 - Suppose that the temperature in degrees Celsius at...Ch. 5.4 - Suppose that the temperature in degrees Fahrenheit...Ch. 5.4 - Show that the volume of a right square pyramid of...Ch. 5.4 - Show that the volume of a regular right hexagonal...Ch. 5.4 - Show that the volume of a regular right hexagonal...Ch. 5.4 - If the charge density at an arbitraiy point (x, y....Ch. 5.5 - Hot air balloons Rot all ballooning is a relaxing....Ch. 5.5 - Hot air balloons Rot all ballooning is a relaxing....Ch. 5.5 - Hot air balloons Rot all ballooning is a relaxing....Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - a. Let B be a cylindrical shell with inner radius...Ch. 5.5 - a. Let B be a cylindrical shell with inner radius...Ch. 5.5 - In the following exercises, the boundaries of the...Ch. 5.5 - In the following exercises, the boundaries of the...Ch. 5.5 - In the following exercises, the boundaries of the...Ch. 5.5 - In the following exercises, the boundaries of the...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - [T] Use a computer algebra system (CAS) to graph...Ch. 5.5 - [T] Use a CAS to graph the solid whose volume is...Ch. 5.5 - 267. Convert the integral into an integral in...Ch. 5.5 - Convert the integral 020x 01 ( xy+z) dzdxdy into...Ch. 5.5 - f(x,y,z)=1,B={(x,y,z)x2+y2+z290,z0}Ch. 5.5 - 270. f(x,y,z)=1x2+y2+z2,B={(x,y,z)x2+y2+z29,y0,z0}Ch. 5.5 - f(x,y,z)=x2+y2. B is bounded above by the...Ch. 5.5 - f(x. y, z) = z. B is bounded above by the half...Ch. 5.5 - Show that if F(,,)=f()g()h() is a continuous...Ch. 5.5 - a. A function F is said to have spherical svmmetiy...Ch. 5.5 - a. Let B be the region between the upper...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - Use spherical coordinates to find the volume of...Ch. 5.5 - Use spherical coordinates to find the volume of...Ch. 5.5 - Convert the integral f44f16 y 216y2f16 x 2 y...Ch. 5.5 - Convert the integral 2f24 x 2f4x2 x 2+ y...Ch. 5.5 - Convert the integral 2f24 x 2f4x2 x 2+ y...Ch. 5.5 - [T] Use a CAS to graph the solid whose volume is...Ch. 5.5 - [T] Use a CAS to graph the solid whose volume is...Ch. 5.5 - [T] Use a CAS to evaluate the integral...Ch. 5.5 - [T] a. Evaluate the integral Ee x 2 + y 2 + z 2...Ch. 5.5 - Express the volume of the solid inside the sphere...Ch. 5.5 - Express the volume of the solid inside the sphere...Ch. 5.5 - The power emitted by an antenna has a power...Ch. 5.5 - Use the preceding exercise to find the total power...Ch. 5.5 - A charge cloud contained in a sphere B of radius r...Ch. 5.5 - Use the preceding exercise to find the total...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - Let Q be the solid unit cube. Find the mass of the...Ch. 5.6 - Let Q be the solid unit hemisphere. Find the mass...Ch. 5.6 - The solid Q of constant density I is situated...Ch. 5.6 - Find the mass of the solid...Ch. 5.6 - Consider the solid Q={(x,y,z)0x1,0y2,0z3} with the...Ch. 5.6 - [T] The solid Q has the mass given by the triple N...Ch. 5.6 - The solid Q is bounded by the planes...Ch. 5.6 - The solid Q is bounded by the planes x+y+z=3 . and...Ch. 5.6 - Let Q be the solid situated outside the sphere...Ch. 5.6 - The mass of a solid is given by 0f20f4x2 x 2+ y...Ch. 5.6 - Let Q be the solid bounded above the cone x2+y2=z2...Ch. 5.6 - The solid Q={(x,y,z)0x2+y216,x0,y0,0zx} has the...Ch. 5.6 - The solid Q is bounded by the cylinder + = a2. the...Ch. 5.6 - Let Q be a solid of constant density k. where k >...Ch. 5.6 - The solid Q has the mass given by the triple...Ch. 5.6 - The solid Q has the moment of inertia Ixabout...Ch. 5.6 - The solid Q has the mass given by the triple...Ch. 5.6 - A solid Q has a volume given by DabdAdz. where D...Ch. 5.6 - Consider the solid enclosed by the cylinder...Ch. 5.6 - [T] The average density of a solid Q is defined as...Ch. 5.6 - Show that the moments of inertia Ix,Iy. and...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformation...Ch. 5.7 - In the following exercises, the transformation...Ch. 5.7 - In the following exercises, the transformation...Ch. 5.7 - In the following exercises, the transformation...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - The triangular region R with the vertices...Ch. 5.7 - The triangular region R with the vertices (0, 0)....Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - The circular annulus sector R bounded by the...Ch. 5.7 - The solid R bounded by the circular cylinder...Ch. 5.7 - Show that Rf( x 2 3 + y 2 3 )dA=21501f()dp. where...Ch. 5.7 - Show that Rf( 16 x 2 +4y+ x 2 )dv=201f()2dp. where...Ch. 5.7 - [T] Find the area of the region bounded by the...Ch. 5.7 - [T] Find the area of the region bounded by the...Ch. 5.7 - Evaluate the triple integral...Ch. 5.7 - Evaluate the triple integral...Ch. 5.7 - A transformation T:R2R2,T(u,v)=(x,y)of the form x...Ch. 5.7 - The transformation T:R2T(u,v)=(x,y) . where...Ch. 5.7 - [T] Find the region S in the uv-plane whose image...Ch. 5.7 - [T] The transformations T : R P. i = 1,.... 4....Ch. 5.7 - [T] The transformation...Ch. 5.7 - [T] Find transformations...Ch. 5.7 - Use the transformation, x=au,y=av,z=cw and...Ch. 5.7 - Find the volume of a football whose shape is a...Ch. 5.7 - [T] Lamé ovals (or superellipses) are plane curves...Ch. 5.7 - [T] Lamé ovals have been consistently used by...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - For the following problems, find the specified...Ch. 5 - For the following problems, find the specified...Ch. 5 - For the following problems, find the specified...Ch. 5 - For the following problems, find the specified...Ch. 5 - For the following problems, find the center of...Ch. 5 - For the following problems, find the center of...Ch. 5 - For the following problems, find the center of...Ch. 5 - For the following problems, find the center of...Ch. 5 - The following problems examine Mount Holly in the...Ch. 5 - The following problems examine Mount Holly in the...Ch. 5 - The following problems consider the temperature...Ch. 5 - [T] The density of Earth’s layers is displayed in...Ch. 5 - The following problems concern the Theorem of...Ch. 5 - The following problems concern the Theorem of...
Additional Math Textbook Solutions
Find more solutions based on key concepts
TRY IT YOURSELF 1
Find the mean of the points scored by the 51 winning teams listed on page 39.
Elementary Statistics: Picturing the World (7th Edition)
Fill in each blank so that the resulting statement is true. Any set of ordered pairs is called a/an ____.The se...
Algebra and Trigonometry (6th Edition)
Derivative Calculations
In Exercises 112, find the first and second derivatives.
University Calculus: Early Transcendentals (4th Edition)
Repeated integration by parts Evaluate the following integrals. 24. e3xcos2xdx
Calculus: Early Transcendentals (2nd Edition)
In Exercises 21–24, use these parameters (based on Data Set 1 “Body Data” in Appendix B):
• Men’s heights are n...
Elementary Statistics (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Your employer automatically puts 5 percent of your salary into a 401(k) retirement account each year. The account earns 10% interest. Suppose you just got the job, your starting salary is $60000, and you expect to receive a 2.5% raise each year. For simplicity, assume that interest earned and your raises are given as nominal rates and compound continuously. Find the value of your retirement account after 20 yearsarrow_forwardCompute the principal values of i¹² (i — 1)² and (i(i − 1))². - -arrow_forward1 2 3 Consider the matrix A = 0 4 5. Give an example of 006 (a) a nonzero matrix B for which det(A + B) = det(A) + det(B); (b) a matrix C for which det(A+C)det(A) + det(C).arrow_forward
- 08:34 ◄ Classroom 07:59 Probs. 5-32/33 D ا. 89 5-34. Determine the horizontal and vertical components of reaction at the pin A and the normal force at the smooth peg B on the member. A 0,4 m 0.4 m Prob. 5-34 F=600 N fr th ar 0. 163586 5-37. The wooden plank resting between the buildings deflects slightly when it supports the 50-kg boy. This deflection causes a triangular distribution of load at its ends. having maximum intensities of w, and wg. Determine w and wg. each measured in N/m. when the boy is standing 3 m from one end as shown. Neglect the mass of the plank. 0.45 m 3 marrow_forwardChapter 4 Quiz 2 As always, show your work. 1) FindΘgivencscΘ=1.045. 2) Find Θ given sec Θ = 4.213. 3) Find Θ given cot Θ = 0.579. Solve the following three right triangles. B 21.0 34.6° ca 52.5 4)c 26° 5) A b 6) B 84.0 a 42° barrow_forwardLet f be a function whose graph consists of 5 line segments and a semicircle as shown in the figure below. Let g(x) = √ƒƒ(t) dt . 0 3 2 -2 2 4 5 6 7 8 9 10 11 12 13 14 15 1. g(0) = 2. g(2) = 3. g(4) = 4. g(6) = 5. g'(3) = 6. g'(13)=arrow_forward
- The expression 3 | (3+1/+1) of the following integrals? A Ов E + + + + 18 3+1+1 3++1 3++1 (A) √2×14 dx x+1 (C) 1½-½√ √ ² ( 14 ) d x (B) √31dx (D) So 3+x -dx is a Riemann sum approximation of which 5 (E) 1½√√3dx 2x+1arrow_forwardExamine the Variables: Carefully review and note the names of all variables in the dataset. Examples of these variables include: Mileage (mpg) Number of Cylinders (cyl) Displacement (disp) Horsepower (hp) Research: Google to understand these variables. Statistical Analysis: Select mpg variable, and perform the following statistical tests. Once you are done with these tests using mpg variable, repeat the same with hp Mean Median First Quartile (Q1) Second Quartile (Q2) Third Quartile (Q3) Fourth Quartile (Q4) 10th Percentile 70th Percentile Skewness Kurtosis Document Your Results: In RStudio: Before running each statistical test, provide a heading in the format shown at the bottom. “# Mean of mileage – Your name’s command” In Microsoft Word: Once you've completed all tests, take a screenshot of your results in RStudio and paste it into a Microsoft Word document. Make sure that snapshots are very clear. You will need multiple snapshots. Also transfer these results to the…arrow_forwardQ4*) (make sure you first understand question P5) Discuss the extremisation of the integral I = = √(2(y + 2) ³y' + (x − 7)) c You may find point (iv) in § 3.5 relevant. dx.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
Double and Triple Integrals; Author: Professor Dave Explains;https://www.youtube.com/watch?v=UubU3U2C8WM;License: Standard YouTube License, CC-BY