Calculus Volume 3
1st Edition
ISBN: 9781630182038
Author: Gilbert Strang, Edwin Jed Herman
Publisher: OpenStax College.
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 5.3, Problem 178E
A spherical cap is the region of a sphere that lies above or below a given plane.
a. Show that the volume of the spherical cap in the figure below is
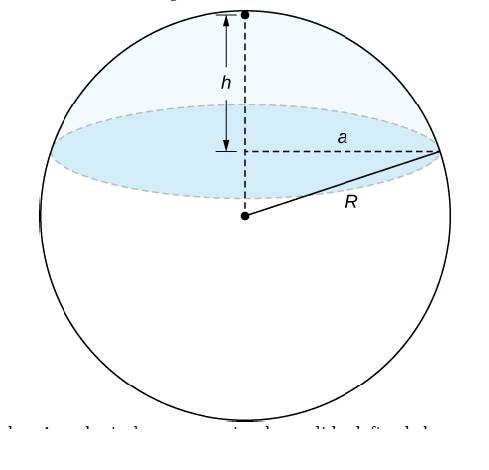
b. A spherical segment is the solid defined by intersecting a sphere with two parallel planes. If the distance between the planes is Ii. show that the volume of the spherical segment in the figure below is
Expert Solution & Answer
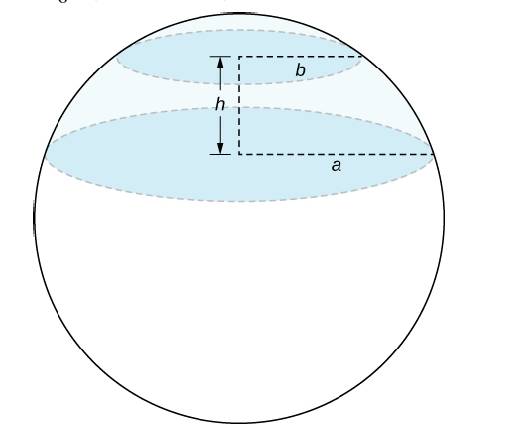
Trending nowThis is a popular solution!
Students have asked these similar questions
B: 18060
msl
Kd
Ka, Sin (n)
I sin ()
sin(30)
Sin (30)
اذا ميريد شرح الكتب بس 0 بالفراغ
3) Cos (30) 0.866
4) Rotating
5) Synchronous speed, 120 x 50
G
5005
1000
s = 1000-950
Copper bosses 5kW
/0001
Rotor input
5
: loo kw
0.05
6) 1
اذا ميريد شرح الكتب فقط ١٥٠
7) rotov
DC
ined sove in Deaper
I need a detailed
solution on paper
please
dy
x+2y-4
=
dx
2x-y-3
Find the general solution of the following equations:
02//yl-4y+13y=esin
1)
R₂ = X2
2) slots per pole per phase = 3/31
B
msl
kd
180
60
Kal Sin (1)
I sin ()
sin(30)
Sin (30)
اذا ميريد شرح الكتب بس 0 بالفراغ
3) Cos (30) 0.866
4) Rotating
5) Synchronous speed, 120 x 50
G
5005
1000
s = 1000-950
Copper bosses 5kW
Rotor input:
5
0.05
loo kw
6) 1
/0001
اذا ميريد شرح الكتب فقط look
7) rotov
DC
ined sove in peaper
I need a detailed
solution on paper
please
Q1// Find the solution of:
'y' = x² +376
x4+316
xyo
Q2 Find the solution of the initial-valued problems:
ex-y
y'
+ex
R₂ = X2
2) slots per pole per phase = 3/31
B-18060
msl
kd
Kasi
Sin (1)
I sin (6)
sin(30)
Sin (30)
اذا ميريد شرح الكتب بس 0 بالفراغ
3) Cos (30) 0.866
4) Rotating
5) Synchronous speed
s = 1000-950
1000
Copper losses: 5kw
Rotor input 5
0.05
6) 1
120 x 50
G
loo kw
ined sove in peaper
I need a detailed
solution on paper
please
Q3// x²y// +xy/ + (x² - ½) y = x³/².
اذا ميريد شرح الكتب فقط look
7) rotor
DC
Q4// x²y// - (2x+x²)y/ + (2 + x)y = x³.
dy
2x+2y+4
=
dx
2x-y-3
Chapter 5 Solutions
Calculus Volume 3
Ch. 5.1 - In the following exercises, use the midpoint rule...Ch. 5.1 - In the following exercises, use the midpoint rule...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...
Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, estimate the volume of...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, calculate the...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - In the following exercises, evaluate the iterated...Ch. 5.1 - function over the given rectangles. 35....Ch. 5.1 - function over the given rectangles. 36....Ch. 5.1 - function over the given rectangles. 37....Ch. 5.1 - function over the given rectangles. 38....Ch. 5.1 - Let f and g be two continuous functions such that...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - Let f and g be two continuous functions such that...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, use property y. of...Ch. 5.1 - In the following exercises, the function f is...Ch. 5.1 - In the following exercises, the function f is...Ch. 5.1 - In the following exercises, the function f is...Ch. 5.1 - In the following exercises, the function f is...Ch. 5.1 - [T] Consider the function f(x,y)=ex2y2where...Ch. 5.1 - [T] Consider the function f(x,y)=sin(x2)cos(y2) ....Ch. 5.1 - In the following exercises, the functions fnare...Ch. 5.1 - In the following exercises, the functions fnare...Ch. 5.1 - In the following exercises, the functions fnare...Ch. 5.1 - In the following exercises, the functions fnare...Ch. 5.1 - An isotherm map is a chart connecting points...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - wIn the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, specify whether the...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - In the following exercises, evaluate the double...Ch. 5.2 - Evaluate the iterated integrals. 80. 012x3x(x+ y...Ch. 5.2 - Evaluate the iterated integrals. 81....Ch. 5.2 - Evaluate the iterated integrals. 82....Ch. 5.2 - Evaluate the iterated integrals. 83....Ch. 5.2 - Evaluate the iterated integrals. 84. 01 1 y 2 1 y...Ch. 5.2 - Evaluate the iterated integrals. 85. 01/2 14 y 2...Ch. 5.2 - Evaluate the iterated integrals. 86. Let D be the...Ch. 5.2 - Evaluate the iterated integrals. 87. Let D be the...Ch. 5.2 - yEvaluate the iterated integrals. 88. a. Show that...Ch. 5.2 - Evaluate the iterated integrals. 89. a. Show that...Ch. 5.2 - The region D bounded by x=0,y=x5+1 , and S y=3x2...Ch. 5.2 - The legion D bounded by y = cos x. y = 4 cos x....Ch. 5.2 - Find the area A(D) of the region...Ch. 5.2 - Let D be the region bounded by y = 1, y = x. y =...Ch. 5.2 - Find the average value of the function f(x. y) =...Ch. 5.2 - Find the average value of the function f(x. y) =-x...Ch. 5.2 - In the following exercises, change the order of...Ch. 5.2 - In the following exercises, change the order of...Ch. 5.2 - In the following exercises, change the order of...Ch. 5.2 - In the following exercises, change the order of...Ch. 5.2 - The region D is shown in the following figure....Ch. 5.2 - The region D is given in the following figure....Ch. 5.2 - Find the volume of the solid under the surface...Ch. 5.2 - Find the volume of the solid tinder the plane...Ch. 5.2 - Find the volume of the solid tinder the plane z=xy...Ch. 5.2 - Find the volume of the solid under the surface z =...Ch. 5.2 - Let g be a positive, increasing, and...Ch. 5.2 - Let g be a positive, increasing, and...Ch. 5.2 - Find the volume of the solid situated in the first...Ch. 5.2 - Find the volume of the solid situated in the first...Ch. 5.2 - Find the volume of the solid bounded by the planes...Ch. 5.2 - Find the volume of the solid bounded by the planes...Ch. 5.2 - Let S1 and S2 , be the solids situated in the...Ch. 5.2 - Let S and 5, be the solids situated in the first...Ch. 5.2 - Let S1 and S2 be the solids situated in the first...Ch. 5.2 - Let S1 and S2 be the solids situated in the first...Ch. 5.2 - [T] The following figure shows the region D...Ch. 5.2 - [T] The region D bounded by the curves y=cosx,x=0...Ch. 5.2 - Suppose that (X. Y) is the outcome of an...Ch. 5.2 - Consider X and Y two random variables of...Ch. 5.2 - [T] The Reuleaux triangle consists of an...Ch. 5.2 - [T] Show that the area of the lunes of Alhazen,...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, express the region D...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, the graph of the polar...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, evaluate the double...Ch. 5.3 - In the following exercises, the integrals have...Ch. 5.3 - In the following exercises, the integrals have...Ch. 5.3 - In the following exercises, the integrals have...Ch. 5.3 - In the following exercises, the integrals have...Ch. 5.3 - In the following exercises, convert the integrals...Ch. 5.3 - In the following exercises, convert the integrals...Ch. 5.3 - In the following exercises, convert the integrals...Ch. 5.3 - In the following exercises, convert the integrals...Ch. 5.3 - Evaluate the integral DffrdAwhere D is the region...Ch. 5.3 - Find the area of the region D bounded by the polar...Ch. 5.3 - Evaluate the integral DrdA, where D is the region...Ch. 5.3 - Find the total area of the region enclosed by the...Ch. 5.3 - Find the area of the region D, which is the region...Ch. 5.3 - Find the area of the region D. which is the region...Ch. 5.3 - Determine the average value of the function f(x....Ch. 5.3 - Determine the average value of the function...Ch. 5.3 - Find the volume of the solid situated in the first...Ch. 5.3 - Find the volume of the solid bounded by the...Ch. 5.3 - a. Find the volume of the solid S1 bounded by the...Ch. 5.3 - a. Find the volume of the solid S1 inside the unit...Ch. 5.3 - For the following two exercises, consider a...Ch. 5.3 - For the following two exercises, consider a...Ch. 5.3 - Find the volume of the solid that lies tinder the...Ch. 5.3 - Find the volume of the solid that lies under the...Ch. 5.3 - Find the volume of the solid that lies under the...Ch. 5.3 - Find the volume of the solid that lies under the...Ch. 5.3 - A radial function f is a function whose value at...Ch. 5.3 - Use the information from the preceding exercise to...Ch. 5.3 - Let f(x,y)=F(r)rbe a continuous radial function...Ch. 5.3 - Apply the preceding exercise to calculate the...Ch. 5.3 - Let f be a continuous function that can be...Ch. 5.3 - Apply the preceding exercise to calculate the...Ch. 5.3 - Let f be a continuous function that can be...Ch. 5.3 - Evaluate Dff arctan (yx)x2+y2dA. where...Ch. 5.3 - A spherical cap is the region of a sphere that...Ch. 5.3 - In statistics, the joint density for two...Ch. 5.3 - The double improper integral e( x2 +y 2/2 )dxdymay...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, change the order of...Ch. 5.4 - In the following exercises, change the order of...Ch. 5.4 - In the following exercises, change the order of...Ch. 5.4 - In the following exercises, change the order of...Ch. 5.4 - Let F. G and H be continuous functions on [a,b]...Ch. 5.4 - Let F. G. and H be differential functions on...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - In the following exercises, evaluate the triple...Ch. 5.4 - The solid E bounded by y2+z2=9,x=0 . x = 5 is...Ch. 5.4 - The solid E bounded by y=x,x=4,y=0 , and z = 1 is...Ch. 5.4 - [T] The volume of a solid E is given by the...Ch. 5.4 - [T] The volume of a solid E is given by the...Ch. 5.4 - In the following exercises, use two circular...Ch. 5.4 - In the following exercises, use two circular...Ch. 5.4 - In the following exercises, use two circular...Ch. 5.4 - In the following exercises, use two circular...Ch. 5.4 - Set up the integral that gives the volume of the...Ch. 5.4 - Set up the integral that gives the volume of the...Ch. 5.4 - Find the average value of the function f(x. y, z)...Ch. 5.4 - Find the average value of the function...Ch. 5.4 - Find the volume of the solid E that lies under the...Ch. 5.4 - Find the volume of the solid E that lies under the...Ch. 5.4 - Consider the pyramid with the base in the xv...Ch. 5.4 - Consider the pyramid with the base in the xy...Ch. 5.4 - The solid E bounded by the sphere of equation...Ch. 5.4 - The solid E bounded by the equation 9x2+4y2+z2=1...Ch. 5.4 - Find the volume of the prism with vertices (0, 0....Ch. 5.4 - Find the volume of the prism with vertices (0. 0....Ch. 5.4 - The solid E bounded by z= 10—2x—y and situated in...Ch. 5.4 - The solid E bounded by z=1x2 and situated in the...Ch. 5.4 - The midpoint rule for the triple integral...Ch. 5.4 - [T] a. Apply the midpoint rule to approximate...Ch. 5.4 - Suppose that the temperature in degrees Celsius at...Ch. 5.4 - Suppose that the temperature in degrees Fahrenheit...Ch. 5.4 - Show that the volume of a right square pyramid of...Ch. 5.4 - Show that the volume of a regular right hexagonal...Ch. 5.4 - Show that the volume of a regular right hexagonal...Ch. 5.4 - If the charge density at an arbitraiy point (x, y....Ch. 5.5 - Hot air balloons Rot all ballooning is a relaxing....Ch. 5.5 - Hot air balloons Rot all ballooning is a relaxing....Ch. 5.5 - Hot air balloons Rot all ballooning is a relaxing....Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - In the following exercises, evaluate the triple...Ch. 5.5 - a. Let B be a cylindrical shell with inner radius...Ch. 5.5 - a. Let B be a cylindrical shell with inner radius...Ch. 5.5 - In the following exercises, the boundaries of the...Ch. 5.5 - In the following exercises, the boundaries of the...Ch. 5.5 - In the following exercises, the boundaries of the...Ch. 5.5 - In the following exercises, the boundaries of the...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - [T] Use a computer algebra system (CAS) to graph...Ch. 5.5 - [T] Use a CAS to graph the solid whose volume is...Ch. 5.5 - 267. Convert the integral into an integral in...Ch. 5.5 - Convert the integral 020x 01 ( xy+z) dzdxdy into...Ch. 5.5 - f(x,y,z)=1,B={(x,y,z)x2+y2+z290,z0}Ch. 5.5 - 270. f(x,y,z)=1x2+y2+z2,B={(x,y,z)x2+y2+z29,y0,z0}Ch. 5.5 - f(x,y,z)=x2+y2. B is bounded above by the...Ch. 5.5 - f(x. y, z) = z. B is bounded above by the half...Ch. 5.5 - Show that if F(,,)=f()g()h() is a continuous...Ch. 5.5 - a. A function F is said to have spherical svmmetiy...Ch. 5.5 - a. Let B be the region between the upper...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, the function f and...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - In the following exercises, find the volume of the...Ch. 5.5 - Use spherical coordinates to find the volume of...Ch. 5.5 - Use spherical coordinates to find the volume of...Ch. 5.5 - Convert the integral f44f16 y 216y2f16 x 2 y...Ch. 5.5 - Convert the integral 2f24 x 2f4x2 x 2+ y...Ch. 5.5 - Convert the integral 2f24 x 2f4x2 x 2+ y...Ch. 5.5 - [T] Use a CAS to graph the solid whose volume is...Ch. 5.5 - [T] Use a CAS to graph the solid whose volume is...Ch. 5.5 - [T] Use a CAS to evaluate the integral...Ch. 5.5 - [T] a. Evaluate the integral Ee x 2 + y 2 + z 2...Ch. 5.5 - Express the volume of the solid inside the sphere...Ch. 5.5 - Express the volume of the solid inside the sphere...Ch. 5.5 - The power emitted by an antenna has a power...Ch. 5.5 - Use the preceding exercise to find the total power...Ch. 5.5 - A charge cloud contained in a sphere B of radius r...Ch. 5.5 - Use the preceding exercise to find the total...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, the region R occupied...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - In the following exercises, consider a lamina...Ch. 5.6 - Let Q be the solid unit cube. Find the mass of the...Ch. 5.6 - Let Q be the solid unit hemisphere. Find the mass...Ch. 5.6 - The solid Q of constant density I is situated...Ch. 5.6 - Find the mass of the solid...Ch. 5.6 - Consider the solid Q={(x,y,z)0x1,0y2,0z3} with the...Ch. 5.6 - [T] The solid Q has the mass given by the triple N...Ch. 5.6 - The solid Q is bounded by the planes...Ch. 5.6 - The solid Q is bounded by the planes x+y+z=3 . and...Ch. 5.6 - Let Q be the solid situated outside the sphere...Ch. 5.6 - The mass of a solid is given by 0f20f4x2 x 2+ y...Ch. 5.6 - Let Q be the solid bounded above the cone x2+y2=z2...Ch. 5.6 - The solid Q={(x,y,z)0x2+y216,x0,y0,0zx} has the...Ch. 5.6 - The solid Q is bounded by the cylinder + = a2. the...Ch. 5.6 - Let Q be a solid of constant density k. where k >...Ch. 5.6 - The solid Q has the mass given by the triple...Ch. 5.6 - The solid Q has the moment of inertia Ixabout...Ch. 5.6 - The solid Q has the mass given by the triple...Ch. 5.6 - A solid Q has a volume given by DabdAdz. where D...Ch. 5.6 - Consider the solid enclosed by the cylinder...Ch. 5.6 - [T] The average density of a solid Q is defined as...Ch. 5.6 - Show that the moments of inertia Ix,Iy. and...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, the function...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, determine whether...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformations...Ch. 5.7 - In the following exercises, the transformation...Ch. 5.7 - In the following exercises, the transformation...Ch. 5.7 - In the following exercises, the transformation...Ch. 5.7 - In the following exercises, the transformation...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - In the following exercises, find the Jacobian J of...Ch. 5.7 - The triangular region R with the vertices...Ch. 5.7 - The triangular region R with the vertices (0, 0)....Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - In the following exercises, use the transformation...Ch. 5.7 - The circular annulus sector R bounded by the...Ch. 5.7 - The solid R bounded by the circular cylinder...Ch. 5.7 - Show that Rf( x 2 3 + y 2 3 )dA=21501f()dp. where...Ch. 5.7 - Show that Rf( 16 x 2 +4y+ x 2 )dv=201f()2dp. where...Ch. 5.7 - [T] Find the area of the region bounded by the...Ch. 5.7 - [T] Find the area of the region bounded by the...Ch. 5.7 - Evaluate the triple integral...Ch. 5.7 - Evaluate the triple integral...Ch. 5.7 - A transformation T:R2R2,T(u,v)=(x,y)of the form x...Ch. 5.7 - The transformation T:R2T(u,v)=(x,y) . where...Ch. 5.7 - [T] Find the region S in the uv-plane whose image...Ch. 5.7 - [T] The transformations T : R P. i = 1,.... 4....Ch. 5.7 - [T] The transformation...Ch. 5.7 - [T] Find transformations...Ch. 5.7 - Use the transformation, x=au,y=av,z=cw and...Ch. 5.7 - Find the volume of a football whose shape is a...Ch. 5.7 - [T] Lamé ovals (or superellipses) are plane curves...Ch. 5.7 - [T] Lamé ovals have been consistently used by...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - True or False? Justify your answer with a proof or...Ch. 5 - For the following problems, find the specified...Ch. 5 - For the following problems, find the specified...Ch. 5 - For the following problems, find the specified...Ch. 5 - For the following problems, find the specified...Ch. 5 - For the following problems, find the center of...Ch. 5 - For the following problems, find the center of...Ch. 5 - For the following problems, find the center of...Ch. 5 - For the following problems, find the center of...Ch. 5 - The following problems examine Mount Holly in the...Ch. 5 - The following problems examine Mount Holly in the...Ch. 5 - The following problems consider the temperature...Ch. 5 - [T] The density of Earth’s layers is displayed in...Ch. 5 - The following problems concern the Theorem of...Ch. 5 - The following problems concern the Theorem of...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Finding Complements. In Exercises 5-8, find the indicated complements.
5. LOL A U.S. Cellular survey of smartph...
Elementary Statistics (13th Edition)
Two dice are thrown. Let E be the event that the sum of the dice is odd, let F be the event that at least one o...
A First Course in Probability (10th Edition)
CHECK POINT 1 Write a word description of the set L = {a, b, c, d, e, f}.
Thinking Mathematically (6th Edition)
Chain Rule using a table Let h(x)= f(g(x)) and p(x) = g(f(x)). Use the table to compute the following derivativ...
Calculus: Early Transcendentals (2nd Edition)
5. Let
Does exist? If so, what is it? If not, why not?
Does exist? If so, what is it? If not, why not?
Does...
University Calculus: Early Transcendentals (4th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- ۳/۱ R2X2 2) slots per pole per phase = 3/31 B, 18060 msl Kas Sin() 1sin() sin(30) Sin (30) kd اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speeds S = 1000-950 1000 Copper bosses 5kw 120*50 loca G Rotor input 5 loo kw 6) 1 0.05 اذا ميريد شرح الكتب فقط lookw 7) rotor DC ined sove in peaper I need a detailed solution on paper please 064 Q1// Find the solution of QI/Find the solution of Inxy= 7357 x+2y³ y' = xy3arrow_forwardR₂ = X2 2) slots per pole per phase 3/31 msl 180 60 Kd Ka Sin (1) Isin (6) sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed, 120*50 1000 6 S = 1000-950 1000 Copper bosses: 5kw Rotor input 5 0.05 : loo kw 6) 1 اذا ميريد شرح الكتب فقط 100 7) rotor DC ined sove in peaper I need a detailed solution on paper please Find the general solution of the following equations: Q2lyl-4y+13y=esinx. Find the general solution of the following equations: " Qly (49) - 16y= 0. 151arrow_forward۳/۱ R₂ = X2 2) slots per pole per phase = 3/31 B-18060 msl kd Kasi Sin (1) I sin (6) sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed s = 1000-950 1000 Copper losses: 5kw Rotor input 5 0.05 6) 1 120 x 50 G loo kw اذا میرید شرح الكتب فقط look 7) rotor DC ined sove in peaper I need a detailed solution on paper dy please 04 12=-cosx.y + 2cosx with y(x) = 1 か 'Oy + xlny + xe")dx + (xsiny + xlnx +*dy=0. 01arrow_forward
- ٣/١ R2X2 2) slots per pole per phase = 3/31 B, 18060 msl kd Kas Sin (1) 1sin() sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speeds S = 1000-950 1000 Copper bosses 5kw 120*50 loca G Rotor input 5 loo kw 0.05 6) 1 اذا ميريد شرح الكتب فقط lookw 7) rotor ined sove in peaper I need a detailed solution on paper please DC 口 04 on its wheels as shown in figure. The the door is 8 m below the free surface o is located at the center of the d no water leaks an accident and lands at the bottom of the lake 12m high and I m wide, and the top edge of water Determine the hydrostatic force on the discuss if the driver can open the door, if ong person can lift 100 kg, the passenger The door can be approximated as a vertical rec | 279|-|(23+2+12+20=2) AA Find the general solution of the following equations: 11 - 1/4+xy/-(1-x²³)= 0. 2arrow_forward۳/۱ : +0 العنوان I need a detailed drawing with explanation R₂ = X2 2) slots per pole per phase 3/31 Le msl 180 60 Kd Ka Sin (1) Isin (6) sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed, 120*50 1000 6 S = 1000-950 1000 Copper bosses: 5kw Rotor input 5 loo kw 0.05 6) 1 اذا ميريد شرح الكتب فقط ١٥٠ 7) rotov DC ined sove in peaper I need a detailed solution on paper please 064 Q1// Find the solution of: ( texty Q1// Find the solution of: '' y' -2y= 22% √y³arrow_forwardR2X2 2) slots per pole per phase = 3/31 B-180-60 msl kd Ka, Sin (1) I sin (6) sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed s = 1000-950 1000 Copper losses 5kw 120 50 G Rotor input 5 loo kw 6) 1 ۳/۱ 0.05 إذا ميريد شرح الكتب فقط look 7) rotov DC ined sove in peaper I need a detailed solution on paper please Find the general solution of the following equations: " yll + 4y = tan2x. Find the general solution of the following equations: 01-24+7=0 T el [A] G ха =T Marrow_forward
- R₂ = X2 2) slots per pole per phase = 3/31 B-18060 msl kd Kasi Sin (1) I sin (6) sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed s = 1000-950 1000 Copper losses: 5kw Rotor input 5 0.05 6) 1 120 x 50 G loo kw اذا میرید شرح الكتب فقط look 7) rotor DC ined sove in peaper I need a detailed solution on paper please 0 64 Solve the following equations: = dx x²+y2 with y(0) = 1. 7357 Solve the following equations: dy x³+3xy² Q1// = dx 3x²y+y³° 01arrow_forward٣/١ R2X2 2) slots per pole per phase = 3/3 1 B18060 msl Kd 3 Kol Sin (1) 1sin() sin(30) Sin (30) اذا میرید شرح الكتب بس 0 بالفراغ 3) cos (30) 0.866 4) Rotating 5) Synchronous speeds 120*50 G looo 1000-950 1000 50:05 Copper losses: 5kw Rotor input 5 loo kw 0.05 6) 1 اذا ميريد شرح الكتب فقط look 7) rotor DC ined sove in peaper I need a detailed solution on paper please 0 64 (Find the solution of the initial-valued problems: xy' + 2y = x³e* ;y(1) = 0 Q1// Find the solution of: (1) y' + ytqpx = see²x y³arrow_forwardA fluid has density 800 kg/m³ and flows with velocity v = xi + yj + zk, where x, y, and z are measured in meters, and the components of u are measured in meters per second. Find the rate of flow outward through the part of the paraboloid z = 64 - x² - y² that lies above the xy plane.arrow_forward
- ۳/۱ : +0 العنوان I need a detailed drawing with explanation R₂ = X2 2) slots per pole per phase 3/31 Le msl 180 60 Kd Ka Sin (1) Isin (6) sin(30) Sin (30) اذا ميريد شرح الكتب بس 0 بالفراغ 3) Cos (30) 0.866 4) Rotating 5) Synchronous speed, 120 x 50 S = 1000-950 1000 Copper bosses: 5kw Rotor input 5 6 : loo kw 6) 1 0.05 اذا ميريد شرح الكتب فقط 100 7) rotor DC 1000 ined sove in peaper I need a detailed solution on paper please // Find the solution of: |(2xy³ + 4x)y' = x²y² + y² 351 // Find the solution of: (1) 2xyy' = 1+ y² 01 175 T Τ Marrow_forwardFind the flux of the vector field F = (y,−x, 2²) through the helicoid with parameterization r(u, v) = (u cos v, u sin v, v) 0 ≤ u≤ 3, 0 ≤v≤ oriented away from the origin.arrow_forwardthey take? 8.1.13 WP GO Tutorial An article in the Journal of Agricultural Science ["The Use of Residual Maximum Likelihood to Model Grain Quality Characteristics of Wheat with Variety, Climatic and Nitrogen Fertilizer Effects” (1997, Vol. 128, pp. 135–142)] investigated means of wheat grain crude protein content (CP) and Hagberg falling number (HFN) surveyed in the United Kingdom. The analysis used a variety of nitrogen fertilizer applications (kg N/ha), temperature (°C), and total monthly rainfall (mm). The following data below describe temperatures for wheat grown at Harper Adams Agricultural College between 1982 and 1993. The temperatures measured in June were obtained as follows: 15.2 14.2 14.0 12.2 14.4 12.5 14.3 14.2 13.5 11.8 15.2 Assume that the standard deviation is known to be σ = 0.5. a. Construct a 99% two-sided confidence interval on the mean temperature. b. Construct a 95% lower-confidence bound on the mean temperature. c. Suppose that you wanted to be 95% confident that…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Area Between The Curve Problem No 1 - Applications Of Definite Integration - Diploma Maths II; Author: Ekeeda;https://www.youtube.com/watch?v=q3ZU0GnGaxA;License: Standard YouTube License, CC-BY