Chapter 5.5, Problem 38E

a.

To determine

To identify: The $f^{\left(4\right)}\text{ for }f\left(x\right)=\sin \left(x^2\right)$ .

Answer to Problem 38E

The required value is $f^{\left(4\right)}\left(x\right)=\left(16x^4-12\right)\sin x^2-48x^2\cos x^2$

Explanation of Solution

Given information:

The given integral is ${\displaystyle \underset{-1}{\overset{1}{\int }}\sin \left(x^2\right)dx}$ .

Consider the given function.

Take the derivative.

  $\begin{array}{c}f\text{'}\left(x\right)=\frac{d}{dx}\sin \left(x^2\right)\\ =2x\cos x^2\end{array}$

Again, take the derivative till the $f^{\left(4\right)}$ .

  $\begin{array}{c}f\text{'}\text{'}\left(x\right)=\frac{d}{dx}\left(2x\cos x^2\right)\\ =2\cos x^2-4x^2\sin x^2\\ f\text{'}\text{'}\text{'}\left(x\right)=\frac{d}{dx}\left(2\cos x^2-4x^2\sin x\right)\\ =-8x^3\cos x^2-12x\sin x^2\\ f\text{'}\text{'}\text{'}\text{'}\left(x\right)=\frac{d}{dx}\left(-8x^3\cos x^2-12x\sin x^2\right)\\ =\left(16x^4-12\right)\sin x^2-48x^2\cos x^2\end{array}$

Therefore, $f^{\left(4\right)}\left(x\right)=\left(16x^4-12\right)\sin x^2-48x^2\cos x^2$

b.

To determine

To graph: The function $y=f^{\left(4\right)}\left(x\right)$ .

Explanation of Solution

Given information:

The given function is $f^{\left(4\right)}\left(x\right)=\left(16x^4-12\right)\sin x^2-48x^2\cos x^2$ .

Graph:

Draw the graph for the function $f^{\left(4\right)}\left(x\right)=\left(16x^4-12\right)\sin x^2-48x^2\cos x^2$ .

Step 1: Open ti-83 calculator press Y= key and enter the above equation.

Step 2: Press WINDOW key and set the window as $[-1,1]\text{ by }\left[-30,10\right]$ , press GRAPH key.

The required graph is shown below:

  

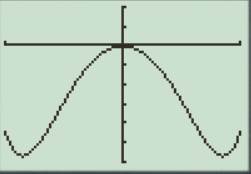
Interpretation: The graph has three inflation point in the interval $[-1,1]$ .

c.

To determine

To identify: Why the graph in part (b) suggests that the given function is $\left|f^{\left(4\right)}\left(x\right)\right|\le 30\text{ for }-1\le x\le 1$ .

Answer to Problem 38E

The modulus of function is less than or equal to 30.

Explanation of Solution

Given information:

The given function is $f^{\left(4\right)}\left(x\right)=\left(16x^4-12\right)\sin x^2-48x^2\cos x^2$ .

Consider the given function.

Observe the graph.

  

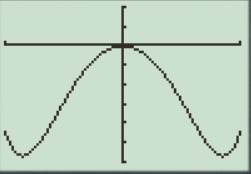
For $-1\le x\le 1$ the value of $-30\le f^{\left(4\right)}\left(x\right)\le 10$ .

Thus, the modulus value is less than or equal to 30.

d.

To determine

To prove: That the error estimate for Simpson’s rule is this case becomes $\left|E_s\right|\le \frac{h^4}{3}$ .

Explanation of Solution

Given information:

The given function is $f^{\left(4\right)}\left(x\right)=\left(16x^4-12\right)\sin x^2-48x^2\cos x^2$ .

Proof:

Consider the given function.

If S represents the approximation to ${\displaystyle \underset{a}{\overset{b}{\int }}f\left(x\right)dx}$ given by the Simpson’s rule, then the errors $E_s$ satisfy.

  $\left|E_s\right|\le \frac{b-a}{180}{h}^4{M}_{f^{\left(4\right)}}$

  $M_{f^{\left(4\right)}}$ , it is maximum value of $\left|f^{\left(4\right)}\right|\text{ on }\left[a,b\right]$ .

Since,

  $\begin{array}{l}\left[a,b\right]=\left[-1,1\right]\\ M_{f^{\left(4\right)}}=30\end{array}$

Thus,

  $\begin{array}{c}\left|E_s\right|\le \frac{1-\left(-1\right)}{180}{h}^4\left(30\right)\\ \le \frac{60}{180}{h}^4\\ \left|E_s\right|\le \frac{h^4}{3}\end{array}$

Hence, proved.

e.

To determine

To prove: That the Simpson’s Rule error will be less than or equal to 0.01 if $h\le 0.4$ .

Explanation of Solution

Given information:

The error estimate for Simpson’s rule is $\left|E_s\right|\le \frac{h^4}{3}$ .

Proof:

Consider the given information.

If $h\le 0.4$

  $\begin{array}{l}\left|E_s\right|\le \frac{h^4}{3}\\ \le \frac{{\left(0.4\right)}^4}{3}\\ \le 0.00853\end{array}$

Thus, error is less than 0.01.

f.

To determine

To identify: How large must n be for $h\le 0.4$ .

Answer to Problem 38E

The required value should be $n\ge 5$ .

Explanation of Solution

Given information:

The given integral is ${\displaystyle \underset{-1}{\overset{1}{\int }}\sin \left(x^2\right)dx}$ .

Consider the given information.

It is known that:

  $\begin{array}{c}h=\frac{b-a}{n}\\ \frac{b-a}{n}\le 0.4\\ n\ge \frac{1-\left(-1\right)}{0.4}\\ n\ge 5\end{array}$ .

Thus, the required value should be $n\ge 5$ .