
Concept explainers

PROBLEM 5.132
The sides and the base of a punch bowl are of uniform thickness t. If t << R and R = 250 mm, determine the location of the center of gravity of (a) the bowl, (b) the bunch.
(a)
The location of the centre of gravity of the bowl.
Answer to Problem 5.132P
The location of the centre of gravity of the bowl is
Explanation of Solution
Refer Fig. P5.132 and Fig. 1.
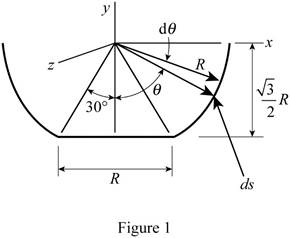
For the coordinate axis given below, using the symmetry of the diagram, determine the x and z coordinates of the centre of gravity.
The bowl can be assumed as a shell, where the centre of gravity coincides with the centroid of the shell.
The element of area is obtained by rotating the arc ds about the y-axis for the walls of the bowl.
Write the expression for the area of the element.
Here,
Write the expression for y coordinate of the centroid of the element.
Here,
Write the expression for
Write the expression for y coordinate of the centre of gravity.
Here,
Conclusion:
Calculate the area using equation (I).
Substitute (I) and (II) in (III).
From figure 1, find the area of the base and distance of the centroid of the base to the y axis.
Substitute equations (V), (VI) and (VII) in equation (IV).
Substitute
Therefore, the location of the centre of gravity of the bowl is
(b)
The location of the centre of gravity of the punch.
Answer to Problem 5.132P
The location of the centre of gravity of the bowl is
Explanation of Solution
Refer Fig. P5.132 and Fig. 2.
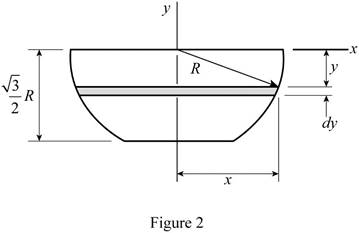
For the coordinate axis given below, using the symmetry of the diagram, determine the x and z coordinates of the centre of gravity.
The punch can be assumed as homogenous, where the centre of gravity coincides with the centroid of the volume.
The element of volume of the disk has radius x and thickness dy.
Find the expression for
Write the expression for the volume of the element.
Here,
Write the expression for y coordinate of the centre of gravity.
Conclusion:
Calculate the volume using equation (IX).
Find
Substitute equations (XI), and (XII) in equation (X).
Substitute
Therefore, the location of the centre of gravity of the bowl is
Want to see more full solutions like this?
Chapter 5 Solutions
VECTOR MECH....F/ENGNRS-STATICS -CONNECT
- The plane region A is submerged in a fluid of weight density . The resultant force of the fluid pressure on the region is R acting at the point C (called the pressure center) located at the distance h below the surface of the fluid. Show that R=Qa and h=Ia/Qa, where Qa and Ia are the first and second moments of A about the axis a-a.arrow_forwardFor the semiannular area of Prob. 5.12, determine the ratio r1 to r2 so that the centroid of the area is located at x = -1/2 r2 and y= 0.(Reference to Problem 5.12):Locate the centroid of the plane area shown.arrow_forwardThe frame of a greenhouse is constructed from uniform aluminum channels. Locate the center of gravity of the position of the frame shown. Consider, r= 3 ft. 5 ft 3 ft Multiple Choice O 2 ft X = 1.750 ft, Y = 4.14 ft, and Z = 2.355 ft. X = 2.750 ft, Y = 6 ft, and Z = 1.355 ft. X = 1.750 ft, Y = 4.14 ft, and Z = 1.355 ft. X = 1.750 ft, Y = 5.14 ft, and Z = 1.355 ft.arrow_forward
- 3.2 Please help me understand and answer this question thank youuuarrow_forwardPlease helparrow_forwardProblem 4.1Given: A barge may be assumed as a rectangular prism (or cuboid) with a length between perpendiculars of 70 ft., a beam of 30 ft., and a depth of ship of 6 ft. The ship weighs 150 tons (US “short ton”) and this weight may be assumed uniformly distributed in the volume of the ship. The following Cargo was loaded along the center line of the ship relative to the deck (top) of the ship. Required: Considering ONLY transverse stability,a) Find the buoyant force and draft of the vessel.arrow_forward
- calculate (a) centroid (b) Check results for n = 2 (c) Calculate Volume of the body obtained by revolving the area about the x axisarrow_forward5.8 Locate the centroid of the plane area shown. 16 in. + 20 in. r = 38 in.arrow_forwardA circular plate with radius r = 0.95 m lies next to a rectangular plate with base br = 0.78 m and height hr = 0.847 m which lies next to a triangular plate with base bt = 1.638 m and height ht = 0.995 m . Determine the common center of gravity in the y-direction of the circular and the rectangular plate if the plates are equally thick and are made of the same material.arrow_forward
- Problem 3. Locate the center of gravity of the steel machine element shown below with respect to x, y, and z axes. r= 1 in. 4 in. 1 in. 6 in. 1 in. 3 in..arrow_forwardDetermine the x coordinate of the centroid of the volume shown. (Hint:The height y of the volume is proportional to the x coordinate; consider an analogy between this height and the water pressure on a submerged surface.)arrow_forward(a) Set up the integration to determine the centroid (b) Calculate the area of the surface obtained by revolving the curve about the x axis (c) Area of the surface obtained by revolving the curve about the y axisarrow_forward
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
