
Concept explainers
Show that as r1 approaches r2, the location of the centroid approaches that for an arc of circle of radius (r1 + r2)/2.
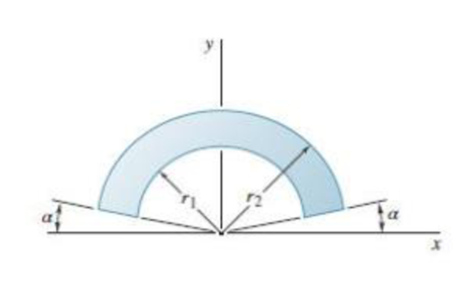
To show that as
Answer to Problem 5.17P
The location of the centroid for an arc of circle of radius
Explanation of Solution
Write the expression for the y-coordinate of the centroid of the sector with radius
Here
Write the expression for the area of the sector with radius
Write the expression for the y-coordinate of the centroid of the sector with radius
Here
Write the expression for the area of the sector with radius
Write the expression for
Substitute (I), (II), (III) and (IV) in the above equation to calculate
Write the expression for
Substitute (II) and (IV) in the above equation to calculate
Write the expression to calculate the y-coordinate of the centroid of the given area.
Substitute (V) and (VI) in the above equation to calculate
Write the expression for the y-coordinate of the centroid with an arc of radius
Rewrite the expression
Let
Substitute the above two expressions in (VIII) to rewrite.
Apply the limits
Rewrite r using
Conclusion:
Substitute (XII) in (VII) to calculate
Therefore, the above expression is same as that of the expression given in (VIII).
Thus, the location of the centroid for an arc of circle of radius
Want to see more full solutions like this?
Chapter 5 Solutions
VECTOR MECH....F/ENGNRS-STATICS -CONNECT
- Using the method of composite areas, find the centroid of the truncated parabolic complement.arrow_forwardFind the centroid of the truncated parabolic complement by integration.arrow_forwardCompute the center of mass/ centroid of the region R = {(x, y): 1 ≤ x ≤ 3, 0 ≤ y ≤ x^2. Show the grapharrow_forward
- Break the shaded area into the five different areas shown. Find the area and the x- and y-coordinates of the centroid for each piece. Enter positive numbers for all answers. Answers: A3 A4 D: A5 i i mm² mm² mm² mm² ५ X1 X2 X3 X4 mm² xs - I 2 I 3 5 mm mm mm mm mm Y₁ Y2 Y3 Y4 Y5 - i i mm mm mm mm mmarrow_forwarddetermine the centroid of the surface given in the figure and its static moment against the X and Y axes of the coordinate system 4m y 2m Xarrow_forwardQ4/A/Locate the centroid (x,y) of the cross-sectional area as shown in figure 5. 125 mm 125 mm 200 mm 200 mm 60 mm 150 mmarrow_forward
- Find the distance ȳ to the centroid of the cross-sectional shape, given: L1 = 460 mm, L2 = 90 mm, L3 = 105 mm, L4 = 100 mm, L5 = 660 mmarrow_forwardLocate the centroid of the cross section below Hint: Cut the cross section into a rectangular shapes and determine thecentroids of the each rectangle. Use the formula AT (X) = A1 (x1) + A2(x2) + A3 (x3) to solve for x and AT (y)= A1(y1) + A2 (y2) + A3y3t o solve for Y. AT = A1+A2 + A3arrow_forwardb - b= 134 mm, r=68 mm For the given composite geometry locate the centroid of the plane area shown The location of the centroid: Along x-direction is: mm. (answer to the nearest whole number) Along y-direction is: mm. (answer to the nearest whole number)arrow_forward
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
