
Rigid Body Nutation. Euler’s equations describe the motion of the principal-axis components of the angular velocity of a freely rotating rigid body (such as a space station), as seen by an observer rotating with the body (the astronauts, for example). This motion is called nutation. If the angular velocity components are denoted by
The trajectory of a solution
a. Show that each trajectory of this system lies on the surface of a (possibly degenerate) sphere centered at the origin
b. Find all the critical points of the system, i.e. all points
c. Show that the trajectories of the system lie along the intersection of a sphere and an elliptic cylinder of the form
d. Using the results of parts (b) and (c), argue that the trajectories of this system are closed curves. What does this say about the corresponding solutions?
e. Figure
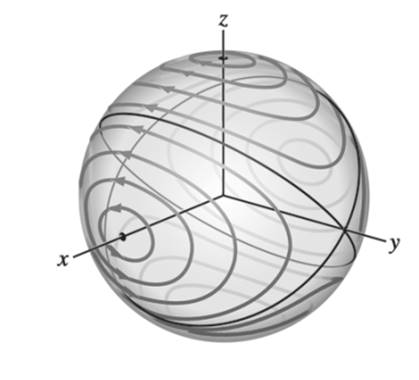
Figure
Want to see the full answer?
Check out a sample textbook solution
Chapter 5 Solutions
Fundamentals of Differential Equations and Boundary Value Problems
- This question builds on an earlier problem. The randomized numbers may have changed, but have your work for the previous problem available to help with this one. A 4-centimeter rod is attached at one end to a point A rotating counterclockwise on a wheel of radius 2 cm. The other end B is free to move back and forth along a horizontal bar that goes through the center of the wheel. At time t=0 the rod is situated as in the diagram at the left below. The wheel rotates counterclockwise at 1.5 rev/sec. At some point, the rod will be tangent to the circle as shown in the third picture. B A B at some instant, the piston will be tangent to the circle (a) Express the x and y coordinates of point A as functions of t: x= 2 cos(3πt) and y= 2 sin(3πt) (b) Write a formula for the slope of the tangent line to the circle at the point A at time t seconds: -cot (3πt) (c) Express the x-coordinate of the right end of the rod at point B as a function of t: 2 cos(3πt) +41/1 (d) Express the slope of the rod…arrow_forwardConsider the proof below: Proposition: If m is an even integer, then 5m +4 is an even integer. Proof: We see that |5m+4=10n+4 = 2(5n+2). Therefore, 5m+4 is an even integer. **Note: you may assume the proof is valid, just poorly written. Based upon the Section 1.3 screencast and the reading assignment, select all writing guidelines that are missing in the proof. Proof begins by stating assumptions ✓ Proof has an invitational tone/uses collective pronouns Proof is written in complete sentences Each step is justified ☐ Proof has a clear conclusionarrow_forwardNote: The purpose of this problem below is to use computational techniques (Excelspreadsheet, Matlab, R, Python, etc.) and code the dynamic programming ideas seen inclass. Please provide the numerical answer to the questions as well as a sample of yourwork (spreadsheet, code file, etc.).We consider an N-period binomial model with the following properties: N = 60, thecurrent stock price is S0 = 1000; on each period, the stock price increases by 0.5% whenit moves up and decreases by 0.3% when it moves down. The annual interest rate on themoney market is 5%. (Notice that this model is a CRR model, which means that thebinomial tree is recombining.)(a) Find the price at time t0 = 0 of a (European) call option with strike price K = 1040and maturity T = 1 year.(b) Find the price at time t0 = 0 of a (European) put option with strike price K = 1040and maturity T = 1 year.(c) We consider now, that you are at time t5 (i.e. after 5 periods, which represents 1month later). Assume that the stock…arrow_forward
- 4. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.5.024. Find the approximations Tη, Mn, and S, to the integral computer algebra system.) ASK YOUR TEACHER PRACTICE ANOTHER 4 39 √ dx for n = 6 and 12. Then compute the corresponding errors ET, EM, and Es. (Round your answers to six decimal places. You may wish to use the sum command on a n Tn Mn Sp 6 12 n ET EM Es 6 12 What observations can you make? In particular, what happens to the errors when n is doubled? As n is doubled, ET and EM are decreased by a factor of about Need Help? Read It ' and Es is decreased by a factor of aboutarrow_forward6. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.5.001. ASK YOUR TEACHER PRACTICE ANOTHER Let I = 4 f(x) dx, where f is the function whose graph is shown. = √ ² F(x 12 4 y f 1 2 (a) Use the graph to find L2, R2 and M2. 42 = R₂ = M₂ = 1 x 3 4arrow_forwardThe general solution X'=Ax is given. Discuss the nature of the solutions in a neighborhood of (0,0) -2-2 (²) |a) A = (23) X(A) = (₁ (fi)e* + (2 (2) eht -2-5arrow_forward
- show work in paperarrow_forwardpractice problem please help!arrow_forwardPlease ensure that all parts of the question are answered thoroughly and clearly. Include a diagram to help explain answers. Make sure the explanation is easy to follow. Would appreciate work done written on paper. Thank you.arrow_forward
- Find a parameterization for a circle of radius 4 with center (-4,-6,-3) in a plane parallel to the yz plane. Write your parameterization so the y component includes a positive cosine.arrow_forwardUsing the method of joints, determine the force in each member of the truss shown. Summarize the results on a force summation diagram, and indicate whether each member is in tension or compression. You may want to try the "quick" method hod.16 8m T or C CD CE AB EF BF гид B 6m i force in CE only (change top force to 8kn) 8 KN 8kNarrow_forwardNo chatgpt pls will upvotearrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
