Fundamentals of Differential Equations and Boundary Value Problems
7th Edition
ISBN: 9780321977106
Author: Nagle, R. Kent
Publisher: Pearson Education, Limited
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5.4, Problem 18E
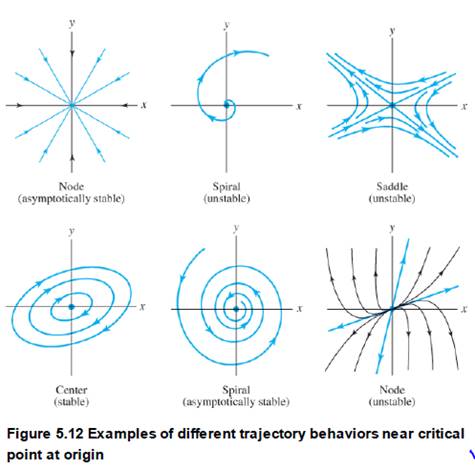
In Problems 15-18, find all critical points for the given system. Then use a software package to sketch the direction field in the phase plane and from this describe the stability of the critical points (i.e., compare with Figure 5.12).
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
3. A different 7-Eleven has a bank of slurpee fountain heads. Their available flavors are as follows: Mountain
Dew, Mountain Dew Code Red, Grape, Pepsi and Mountain Dew Livewire. You fill five different cups full
with each type of flavor. How many different ways can you arrange the cups in a line if exactly two Mountain
Dew flavors are next to each other?
3.2.1
Business
What is the area of this figure?
5 mm
4 mm
3 mm
square millimeters
11 mm
Submit
8 mm
Work it out
9 mm
Chapter 5 Solutions
Fundamentals of Differential Equations and Boundary Value Problems
Ch. 5.2 - Let A=D1, B=D+2, C=D2+D2, where D=d/dt. For y=t38,...Ch. 5.2 - Show that the operator (D1)(D+2) is the same as...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...
Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - Prob. 14ECh. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - Prob. 16ECh. 5.2 - Prob. 17ECh. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 19-21, solve the given initial value...Ch. 5.2 - In Problems 19-21, solve the given initial value...Ch. 5.2 - Prob. 21ECh. 5.2 - Prob. 22ECh. 5.2 - Prob. 23ECh. 5.2 - Prob. 24ECh. 5.2 - In Problems 25-28, use the elimination method to...Ch. 5.2 - Prob. 26ECh. 5.2 - Prob. 27ECh. 5.2 - Prob. 28ECh. 5.2 - Prob. 29ECh. 5.2 - Prob. 30ECh. 5.2 - Two large tanks, each holding 100L of liquid, are...Ch. 5.2 - In Problem 31, 3L/min of liquid flowed from tank A...Ch. 5.2 - In Problem 31, assume that no solution flows out...Ch. 5.2 - Feedback System with Pooling Delay. Many physical...Ch. 5.2 - Arms Race. A simplified mathematical model for an...Ch. 5.2 - Let A, B, and C represent three linear...Ch. 5.3 - In Problems 1-7, convert the given initial value...Ch. 5.3 - In Problems 1-7, convert the given initial value...Ch. 5.3 - In Problems 1-7, convert the given initial value...Ch. 5.3 - In Problems 1-7, convert the given initial value...Ch. 5.3 - In Problems 1-7, convert the given initial value...Ch. 5.3 - In Problems 1-7, convert the given initial value...Ch. 5.3 - In Problems 1-7, convert the given initial value...Ch. 5.3 - Prob. 8ECh. 5.3 - In Section 3.6, we discussed the improved Eulers...Ch. 5.3 - In Problems 10-13, use the vectorized Euler method...Ch. 5.3 - In Problems 10-13, use the vectorized Euler method...Ch. 5.3 - In Problems 10-13, use the vectorized Euler method...Ch. 5.3 - In Problems 10-13, use the vectorized Euler method...Ch. 5.3 - Prob. 14ECh. 5.3 - In Problems 14-24, you will need a computer and a...Ch. 5.3 - In Problems 14-24, you will need a computer and a...Ch. 5.3 - Prob. 18ECh. 5.3 - Prob. 19ECh. 5.3 - In Problems 14-24, you will need a computer and a...Ch. 5.3 - Prob. 21ECh. 5.3 - Prob. 22ECh. 5.3 - Prob. 24ECh. 5.3 - Prob. 25ECh. 5.3 - Prob. 26ECh. 5.3 - Prob. 27ECh. 5.3 - Prob. 28ECh. 5.3 - In Problems 25-30, use a software package or the...Ch. 5.3 - Prob. 30ECh. 5.4 - In Problems 1 and 2, verify that the pair x(t),...Ch. 5.4 - In Problems 1 and 2, verify that pair x(t), y(t)...Ch. 5.4 - In Problems 3-6, find the critical point set for...Ch. 5.4 - Prob. 4ECh. 5.4 - In Problems 3-6, find the critical point set for...Ch. 5.4 - In Problems 3-6, find the critical point set for...Ch. 5.4 - In Problems 7-9, solve the related phase plane...Ch. 5.4 - In Problems 7-9, solve the related phase plane...Ch. 5.4 - In Problems 7-9, solve the related phase plane...Ch. 5.4 - Find all the critical points of the system...Ch. 5.4 - In Problems 11-14, solve the related phase plane...Ch. 5.4 - In Problems 11-14, solve the related phase plane...Ch. 5.4 - In Problems 11-14, solve the related phase plane...Ch. 5.4 - In Problems 11-14, solve the related phase plane...Ch. 5.4 - In Problems 15-18, find all critical points for...Ch. 5.4 - In Problems 15-18, find all critical points for...Ch. 5.4 - In Problems 15-18, find all critical points for...Ch. 5.4 - In Problems 15-18, find all critical points for...Ch. 5.4 - In Problems 19-24, convert the given second-order...Ch. 5.4 - In Problems 19-24, convert the given second-order...Ch. 5.4 - Prob. 21ECh. 5.4 - In Problems 19-24, convert the given second-order...Ch. 5.4 - Prob. 23ECh. 5.4 - In Problems 19-24, convert the given second-order...Ch. 5.4 - Prob. 25ECh. 5.4 - Prob. 26ECh. 5.4 - Prob. 27ECh. 5.4 - Prob. 28ECh. 5.4 - A proof of Theorem 1, page 266, is outlined below....Ch. 5.4 - Phase plane analysis provides a quick derivation...Ch. 5.4 - Prob. 32ECh. 5.4 - Prob. 34ECh. 5.4 - Sticky Friction. An alternative for the damping...Ch. 5.4 - Rigid Body Nutation. Eulers equations describe the...Ch. 5.5 - Radioisotopes and Cancer Detection. A radioisotope...Ch. 5.5 - Secretion of Hormones. The secretion of hormones...Ch. 5.5 - Prove that the critical point (8) of the...Ch. 5.5 - Suppose for a certain disease described by the SIR...Ch. 5.5 - Prob. 6ECh. 5.5 - Prob. 7ECh. 5.5 - Prob. 8ECh. 5.5 - Prob. 9ECh. 5.5 - Prove that the infected population I(t) in the SIR...Ch. 5.6 - Two springs and two masses are attached in a...Ch. 5.6 - Determine the equations of motion for the two...Ch. 5.6 - Four springs with the same spring constant and...Ch. 5.6 - Two springs, two masses, and a dashpot are...Ch. 5.6 - Referring to the coupled mass-spring system...Ch. 5.6 - Prob. 7ECh. 5.6 - A double pendulum swinging in a vertical plane...Ch. 5.6 - Prob. 9ECh. 5.6 - Suppose the coupled mass-spring system of Problem...Ch. 5.7 - An RLC series circuit has a voltage source given...Ch. 5.7 - An RLC series circuit has a voltage source given...Ch. 5.7 - Prob. 3ECh. 5.7 - An LC series circuit has a voltage source given by...Ch. 5.7 - An RLC series circuit has a voltage source given...Ch. 5.7 - Show that when the voltage source in (4) is of the...Ch. 5.7 - Prob. 7ECh. 5.7 - Prob. 8ECh. 5.7 - Prob. 9ECh. 5.7 - Prob. 10ECh. 5.7 - In Problems 10-13, find a system of differential...Ch. 5.7 - In Problems 10-13, find a system of differential...Ch. 5.7 - In Problems 10-13, find a system of differential...Ch. 5.8 - A software package that supports the construction...Ch. 5.8 - Prob. 2ECh. 5.8 - A software package that supports the construction...Ch. 5.8 - Prob. 4ECh. 5.8 - Prob. 5ECh. 5.8 - A software package that supports the construction...Ch. 5.8 - Prob. 11ECh. 5.RP - In Problems 1-4, find a general solution x(t),...Ch. 5.RP - In Problems 1-4, find a general solution x(t),...Ch. 5.RP - In Problems 1-4, find a general solution x(t),...Ch. 5.RP - In Problems 1-4, find a general solution x(t),...Ch. 5.RP - Prob. 5RPCh. 5.RP - Prob. 6RPCh. 5.RP - Prob. 7RPCh. 5.RP - Prob. 8RPCh. 5.RP - Prob. 9RPCh. 5.RP - Prob. 10RPCh. 5.RP - Prob. 11RPCh. 5.RP - Prob. 12RPCh. 5.RP - Prob. 13RPCh. 5.RP - Prob. 14RPCh. 5.RP - Prob. 15RPCh. 5.RP - Prob. 16RPCh. 5.RP - Prob. 17RPCh. 5.RP - In the coupled mass-spring system depicted in...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- No chatgpt pls will upvotearrow_forwardFind all solutions of the polynomial congruence x²+4x+1 = 0 (mod 143). (The solutions of the congruence x² + 4x+1=0 (mod 11) are x = 3,4 (mod 11) and the solutions of the congruence x² +4x+1 = 0 (mod 13) are x = 2,7 (mod 13).)arrow_forwardhttps://www.hawkeslearning.com/Statistics/dbs2/datasets.htmlarrow_forward
- Determine whether each function is an injection and determine whether each is a surjection.The notation Z_(n) refers to the set {0,1,2,...,n-1}. For example, Z_(4)={0,1,2,3}. f: Z_(6) -> Z_(6) defined by f(x)=x^(2)+4(mod6). g: Z_(5) -> Z_(5) defined by g(x)=x^(2)-11(mod5). h: Z*Z -> Z defined by h(x,y)=x+2y. j: R-{3} -> R defined by j(x)=(4x)/(x-3).arrow_forwardDetermine whether each function is an injection and determine whether each is a surjection.arrow_forwardLet A = {a, b, c, d}, B = {a,b,c}, and C = {s, t, u,v}. Draw an arrow diagram of a function for each of the following descriptions. If no such function exists, briefly explain why. (a) A function f : AC whose range is the set C. (b) A function g: BC whose range is the set C. (c) A function g: BC that is injective. (d) A function j : A → C that is not bijective.arrow_forward
- Let f:R->R be defined by f(x)=x^(3)+5.(a) Determine if f is injective. why?(b) Determine if f is surjective. why?(c) Based upon (a) and (b), is f bijective? why?arrow_forwardLet f:R->R be defined by f(x)=x^(3)+5.(a) Determine if f is injective.(b) Determine if f is surjective. (c) Based upon (a) and (b), is f bijective?arrow_forwardPlease as many detarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Intro to the Laplace Transform & Three Examples; Author: Dr. Trefor Bazett;https://www.youtube.com/watch?v=KqokoYr_h1A;License: Standard YouTube License, CC-BY