
Rigid Body Nutation. Euler’s equations describe the motion of the principal-axis components of the angular velocity of a freely rotating rigid body (such as a space station), as seen by an observer rotating with the body (the astronauts, for example). This motion is called nutation. If the angular velocity components are denoted by
The trajectory of a solution
a. Show that each trajectory of this system lies on the surface of a (possibly degenerate) sphere centered at the origin
b. Find all the critical points of the system, i.e. all points
c. Show that the trajectories of the system lie along the intersection of a sphere and an elliptic cylinder of the form
d. Using the results of parts (b) and (c), argue that the trajectories of this system are closed curves. What does this say about the corresponding solutions?
e. Figure
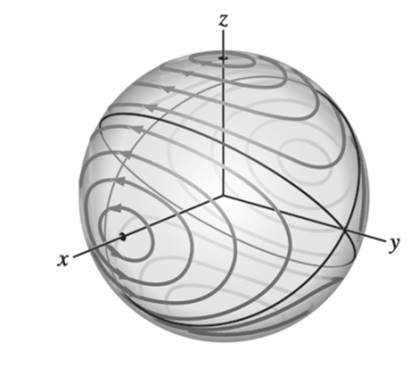
Figure
Want to see the full answer?
Check out a sample textbook solution
Chapter 5 Solutions
Pearson eText Fundamentals of Differential Equations with Boundary Value Problems -- Instant Access (Pearson+)
- how could the bar graph have been organized differently to make it easier to compare opinion changes within political partiesarrow_forwardketch a graph of the function f(x) = 3 cos (표) 6. x +1 5 4 3 3 80 9 2+ 1 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3+ -4 5 -6+ Clear All Draw: пи > Next Questionarrow_forwardDraw the following graph on the interval πT 5π < x < 2 2 y = 2 sin (2(x+7)) 6. 5. 4 3 3 2 1 +3 /2 -π/3 -π/6 π/6 π/3 π/2 2π/3 5π/6 π 7π/6 4π/3 3π/2 5π/311π/6 2π 13π/67π/3 5π Clear All Draw:arrow_forward
- Let f : X → Y and g : Y → Z be two functions. Prove that(1) if g ◦ f is injective, then f is injective; (2) if g ◦ f is surjective, then g is surjective.arrow_forwardketch a graph of the function f(x) = 3 cos (표) 6. x +1 5 4 3 3 80 9 2+ 1 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3+ -4 5 -6+ Clear All Draw: пи > Next Questionarrow_forwardSolve the following boundary value problem using method of separation of variables ди 11.07 (137) 1 J²u + = = 0, -Пarrow_forward3 2 20-10-18-17-16-15-14-13-12-11-10-9 -8 -7 -6 -$4-3-2-1 -1 -2 -3 4- -5+ The curve above is the graph of a sinusoidal function. It goes through the points (-8, -4) and (6,-4). Find a sinusoidal function that matches the given graph. If needed, you can enter π=3.1416... as 'pi' in your answer, otherwise use at least 3 decimal digits. f(x) = > Next Question Barrow_forwardX Grades for X Assignmen X A-Z Datab XE Biocultural X EBSCO-Ful X Review es/119676/assignments/3681238 Review Quiz 8.1-p2 points possible Answered: 3/5 ● Question 1 4+ 3. 2 1 13 /12-11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 -1 -2 -3 -4- 5 2 6 The curve above is the graph of a sinusoidal function. It goes through the points (-7,0) and (3,0). Find a sinusoidal function that matches the given graph. If needed, you can enter π=3.1416... as 'pi' in your answer, otherwise use at least 3 decimal digits. f(x) = > Next Question 申 J % F 刀 Q Search S € t ח Y 7 I * 00 J ப I Darrow_forward2 d) Draw the following graph on the interval k 5π Next Questionarrow_forwardDraw the following graph on the interval 5л Next Questionarrow_forwardDetermine whether the lines L₁ (t) = (-2,3, −1)t + (0,2,-3) and L2 p(s) = (2, −3, 1)s + (-10, 17, -8) intersect. If they do, find the point of intersection.arrow_forwardConvert the line given by the parametric equations y(t) Enter the symmetric equations in alphabetic order. (x(t) = -4+6t = 3-t (z(t) = 5-7t to symmetric equations.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
