Pearson eText Fundamentals of Differential Equations with Boundary Value Problems -- Instant Access (Pearson+)
7th Edition
ISBN: 9780137394524
Author: R. Nagle, Edward Saff
Publisher: PEARSON+
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5.4, Problem 16E
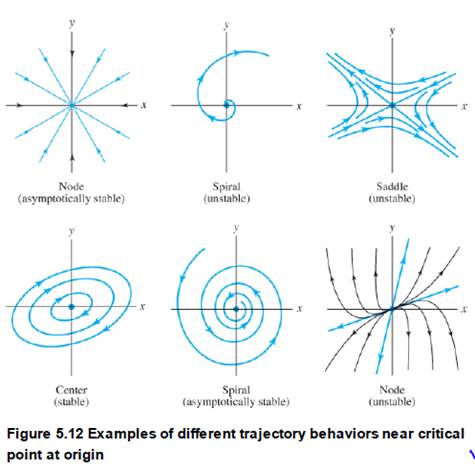
In Problems 15-18, find all critical points for the given system. Then use a software package to sketch the direction field in the phase plane and from this describe the stability of the critical points (i.e., compare with Figure 5.12).
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Topic: Group Theory | Abstract Algebra
Question:
Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe
the number of Sylow subgroups for each.
Instructions:
•
Use Sylow's Theorems (existence, conjugacy, and counting).
•
List divisors of 45 and compute possibilities for n for p = 3 and p = 5.
Show that if n = 1, the subgroup is normal.
Conclude about group structure using your analysis.
Topic: Group Theory | Abstract Algebra
Question:
Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe
the number of Sylow subgroups for each.
Instructions:
•
Use Sylow's Theorems (existence, conjugacy, and counting).
•
List divisors of 45 and compute possibilities for n for p = 3 and p = 5.
Show that if n = 1, the subgroup is normal.
Conclude about group structure using your analysis.
Complete solution required
Chapter 5 Solutions
Pearson eText Fundamentals of Differential Equations with Boundary Value Problems -- Instant Access (Pearson+)
Ch. 5.2 - Let A=D1, B=D+2, C=D2+D2, where D=d/dt. For y=t38,...Ch. 5.2 - Show that the operator (D1)(D+2) is the same as...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...
Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - Prob. 14ECh. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - Prob. 16ECh. 5.2 - Prob. 17ECh. 5.2 - In Problems 3-18, use the elimination method to...Ch. 5.2 - In Problems 19-21, solve the given initial value...Ch. 5.2 - In Problems 19-21, solve the given initial value...Ch. 5.2 - Prob. 21ECh. 5.2 - Prob. 22ECh. 5.2 - Prob. 23ECh. 5.2 - Prob. 24ECh. 5.2 - In Problems 25-28, use the elimination method to...Ch. 5.2 - Prob. 26ECh. 5.2 - Prob. 27ECh. 5.2 - Prob. 28ECh. 5.2 - Prob. 29ECh. 5.2 - Prob. 30ECh. 5.2 - Two large tanks, each holding 100L of liquid, are...Ch. 5.2 - In Problem 31, 3L/min of liquid flowed from tank A...Ch. 5.2 - In Problem 31, assume that no solution flows out...Ch. 5.2 - Feedback System with Pooling Delay. Many physical...Ch. 5.2 - Arms Race. A simplified mathematical model for an...Ch. 5.2 - Let A, B, and C represent three linear...Ch. 5.3 - In Problems 1-7, convert the given initial value...Ch. 5.3 - In Problems 1-7, convert the given initial value...Ch. 5.3 - In Problems 1-7, convert the given initial value...Ch. 5.3 - In Problems 1-7, convert the given initial value...Ch. 5.3 - In Problems 1-7, convert the given initial value...Ch. 5.3 - In Problems 1-7, convert the given initial value...Ch. 5.3 - In Problems 1-7, convert the given initial value...Ch. 5.3 - Prob. 8ECh. 5.3 - In Section 3.6, we discussed the improved Eulers...Ch. 5.3 - In Problems 10-13, use the vectorized Euler method...Ch. 5.3 - In Problems 10-13, use the vectorized Euler method...Ch. 5.3 - In Problems 10-13, use the vectorized Euler method...Ch. 5.3 - In Problems 10-13, use the vectorized Euler method...Ch. 5.3 - Prob. 14ECh. 5.3 - In Problems 14-24, you will need a computer and a...Ch. 5.3 - In Problems 14-24, you will need a computer and a...Ch. 5.3 - Prob. 18ECh. 5.3 - Prob. 19ECh. 5.3 - In Problems 14-24, you will need a computer and a...Ch. 5.3 - Prob. 21ECh. 5.3 - Prob. 22ECh. 5.3 - Prob. 24ECh. 5.3 - Prob. 25ECh. 5.3 - Prob. 26ECh. 5.3 - Prob. 27ECh. 5.3 - Prob. 28ECh. 5.3 - In Problems 25-30, use a software package or the...Ch. 5.3 - Prob. 30ECh. 5.4 - In Problems 1 and 2, verify that the pair x(t),...Ch. 5.4 - In Problems 1 and 2, verify that pair x(t), y(t)...Ch. 5.4 - In Problems 3-6, find the critical point set for...Ch. 5.4 - Prob. 4ECh. 5.4 - In Problems 3-6, find the critical point set for...Ch. 5.4 - In Problems 3-6, find the critical point set for...Ch. 5.4 - In Problems 7-9, solve the related phase plane...Ch. 5.4 - In Problems 7-9, solve the related phase plane...Ch. 5.4 - In Problems 7-9, solve the related phase plane...Ch. 5.4 - Find all the critical points of the system...Ch. 5.4 - In Problems 11-14, solve the related phase plane...Ch. 5.4 - In Problems 11-14, solve the related phase plane...Ch. 5.4 - In Problems 11-14, solve the related phase plane...Ch. 5.4 - In Problems 11-14, solve the related phase plane...Ch. 5.4 - In Problems 15-18, find all critical points for...Ch. 5.4 - In Problems 15-18, find all critical points for...Ch. 5.4 - In Problems 15-18, find all critical points for...Ch. 5.4 - In Problems 15-18, find all critical points for...Ch. 5.4 - In Problems 19-24, convert the given second-order...Ch. 5.4 - In Problems 19-24, convert the given second-order...Ch. 5.4 - Prob. 21ECh. 5.4 - In Problems 19-24, convert the given second-order...Ch. 5.4 - Prob. 23ECh. 5.4 - In Problems 19-24, convert the given second-order...Ch. 5.4 - Prob. 25ECh. 5.4 - Prob. 26ECh. 5.4 - Prob. 27ECh. 5.4 - Prob. 28ECh. 5.4 - A proof of Theorem 1, page 266, is outlined below....Ch. 5.4 - Phase plane analysis provides a quick derivation...Ch. 5.4 - Prob. 32ECh. 5.4 - Prob. 34ECh. 5.4 - Sticky Friction. An alternative for the damping...Ch. 5.4 - Rigid Body Nutation. Eulers equations describe the...Ch. 5.5 - Radioisotopes and Cancer Detection. A radioisotope...Ch. 5.5 - Secretion of Hormones. The secretion of hormones...Ch. 5.5 - Prove that the critical point (8) of the...Ch. 5.5 - Suppose for a certain disease described by the SIR...Ch. 5.5 - Prob. 6ECh. 5.5 - Prob. 7ECh. 5.5 - Prob. 8ECh. 5.5 - Prob. 9ECh. 5.5 - Prove that the infected population I(t) in the SIR...Ch. 5.6 - Two springs and two masses are attached in a...Ch. 5.6 - Determine the equations of motion for the two...Ch. 5.6 - Four springs with the same spring constant and...Ch. 5.6 - Two springs, two masses, and a dashpot are...Ch. 5.6 - Referring to the coupled mass-spring system...Ch. 5.6 - Prob. 7ECh. 5.6 - A double pendulum swinging in a vertical plane...Ch. 5.6 - Prob. 9ECh. 5.6 - Suppose the coupled mass-spring system of Problem...Ch. 5.7 - An RLC series circuit has a voltage source given...Ch. 5.7 - An RLC series circuit has a voltage source given...Ch. 5.7 - Prob. 3ECh. 5.7 - An LC series circuit has a voltage source given by...Ch. 5.7 - An RLC series circuit has a voltage source given...Ch. 5.7 - Show that when the voltage source in (4) is of the...Ch. 5.7 - Prob. 7ECh. 5.7 - Prob. 8ECh. 5.7 - Prob. 9ECh. 5.7 - Prob. 10ECh. 5.7 - In Problems 10-13, find a system of differential...Ch. 5.7 - In Problems 10-13, find a system of differential...Ch. 5.7 - In Problems 10-13, find a system of differential...Ch. 5.8 - A software package that supports the construction...Ch. 5.8 - Prob. 2ECh. 5.8 - A software package that supports the construction...Ch. 5.8 - Prob. 4ECh. 5.8 - Prob. 5ECh. 5.8 - A software package that supports the construction...Ch. 5.8 - Prob. 11ECh. 5.RP - In Problems 1-4, find a general solution x(t),...Ch. 5.RP - In Problems 1-4, find a general solution x(t),...Ch. 5.RP - In Problems 1-4, find a general solution x(t),...Ch. 5.RP - In Problems 1-4, find a general solution x(t),...Ch. 5.RP - Prob. 5RPCh. 5.RP - Prob. 6RPCh. 5.RP - Prob. 7RPCh. 5.RP - Prob. 8RPCh. 5.RP - Prob. 9RPCh. 5.RP - Prob. 10RPCh. 5.RP - Prob. 11RPCh. 5.RP - Prob. 12RPCh. 5.RP - Prob. 13RPCh. 5.RP - Prob. 14RPCh. 5.RP - Prob. 15RPCh. 5.RP - Prob. 16RPCh. 5.RP - Prob. 17RPCh. 5.RP - In the coupled mass-spring system depicted in...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Topic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardTopic: Group Theory | Abstract Algebra Question: Let G be a finite group of order 45. Prove that G has a normal subgroup of order 5 or order 9, and describe the number of Sylow subgroups for each. Instructions: • Use Sylow's Theorems (existence, conjugacy, and counting). • List divisors of 45 and compute possibilities for n for p = 3 and p = 5. Show that if n = 1, the subgroup is normal. Conclude about group structure using your analysis.arrow_forwardDo with graph of the regionarrow_forward
- can you explain why my answer to Q2 was wrong and, how to get the correct answerarrow_forwardProblem 9: The 30-kg pipe is supported at A by a system of five cords. Determine the force in each cord for equilibrium. B 60º A E Harrow_forwardSolve questions by Course Name (Ordinary Differential Equations II 2)arrow_forward
- d((x, y), (z, w)) = |xz|+|yw|, show that whether d is a metric on R² or not?. Q3/Let R be a set of real number and d: R² x R² → R such that -> d((x, y), (z, w)) = max{\x - zl, ly - w} show that whether d is a metric on R² or not?. Q4/Let X be a nonempty set and d₁, d₂: XXR are metrics on X let d3,d4, d5: XX → R such that d3(x, y) = 4d2(x, y) d4(x, y) = 3d₁(x, y) +2d2(x, y) d5(x,y) = 2d₁ (x,y))/ 1+ 2d₂(x, y). Show that whether d3, d4 and d5 are metric on X or not?arrow_forwardplease Solve questions by Course Name( Ordinary Differential Equations II 2)arrow_forwardBusiness discussarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Intro to the Laplace Transform & Three Examples; Author: Dr. Trefor Bazett;https://www.youtube.com/watch?v=KqokoYr_h1A;License: Standard YouTube License, CC-BY