Chapter 5.3, Problem 122AYU

120. Current in an RC Circuit The equation governing the amount of current I (in amperes) after lime t (in microseconds) in a single RC circuit consisting of a resistance R (in ohms), a capacitance C (in microfarads), and an electromotive force E (in volts) is

$I = \frac{E}{R}{e}^{-t/(RC)}$

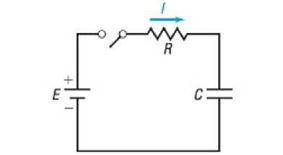
(a) If $E = 120$ volts, $R = 2000$ ohms, and $C = 1.0$ microfarad, how much current I₁ is flowing initially ( $t = 0$)? After 1000 microseconds? After 3000 microseconds?

(b) What is the maximum current?

(c) Graph this function $I = I_1$ (t), measuring I along the $y\text{-axis}$ and t along the $x\text{-axis}$.

(d) If $E = 120$ volts, $R=1000$ ohms, and $C = 2.0$ microfarads, how much current I₂ is flowing initially? After 1000 microseconds? After 3000 microseconds?

(e) What is the maximum current?

(f) Graph the function $I = I_2\left(t\right)$ on the same coordinate axes as $I_1(t)$.