
Mathematical Excursions (MindTap Course List)
4th Edition
ISBN: 9781305965584
Author: Richard N. Aufmann, Joanne Lockwood, Richard D. Nation, Daniel K. Clegg
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 5.2, Problem 8ES
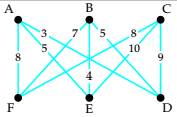
Use trial and error to find two Hamiltonian circuits of different total weights, starting at vertex A in the weighted graph. Compute the total weight of each circuit.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
PQ17
Three components are connected to form a system as shown in the accompanying diagram. Because the components in the 2-3 subsystem are connected in parallel, that subsystem will function if at least one of the two individual components functions. For the entire system to function, component 1 must function and so must the 2-3 subsystem.
The experiment consists of determining the condition of each component [S (success) for a functioning component and F (failure) for a nonfunctioning component]. (Enter your answers in set notation. Enter EMPTY or for the empty set.)
(a) Which outcomes are contained in the event A that exactly two of the three components function?
A =
(b) Which outcomes are contained in the event B that at least two of the components function?
B =
(c) Which outcomes are contained in the event C that the system functions?
C =
(d) List outcomes in C'.
C' =
List outcomes in AU C.
AUC =
List outcomes in A n C.
An C =
List outcomes in BU C.
BUC =
List outcomes in B n C.
BnC=
Three components are connected to form a system as shown in the accompanying diagram. Because the components in the 2-3
subsystem are connected in parallel, that subsystem will function if at least one of the two individual components functions. For the
entire system to function, component 1 must function and so must the 2-3 subsystem.
2
The experiment consists of determining the condition of each component [S (success) for a functioning component and F (failure)
for a nonfunctioning component]. (Enter your answers in set notation. Enter EMPTY or for the empty set.)
(a) Which outcomes are contained in the event A that exactly two of the three components function?
A =
x
(b) Which outcomes are contained in the event B that at least two of the components function?
B =
(c) Which outcomes are contained in the event C that the system functions?
C =
(d) List outcomes in C'.
C' =
List outcomes in A u C.
AUC=
List outcomes in An C.
An C=
List outcomes in Bu C.
BUC=
List outcomes in B n C..
BAC…
Chapter 5 Solutions
Mathematical Excursions (MindTap Course List)
Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - Explain why the following pen-tracing puzzle is...Ch. 5.1 - Transportation An X in the table below indicates a...Ch. 5.1 - Transportation The table below shows the nonstop...Ch. 5.1 - Social Network A group of friends is represented...Ch. 5.1 - Prob. 4ESCh. 5.1 - Determine (a) the number of edges in the graph,...
Ch. 5.1 - Determine (a) the number of edges in the graph,...Ch. 5.1 - Determine (a) the number of edges in the graph,...Ch. 5.1 - Determine (a) the number of edges in the graph,...Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Explain why the following two graphs cannot be...Ch. 5.1 - Label the vertices of the second graph so that it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - Parks in Exercises 23 and 24, a map of a park is...Ch. 5.1 - Parks in Exercises 23 and 24, a map of a park is...Ch. 5.1 - Transportation For the train routes given in...Ch. 5.1 - Transportation For the direct air flights given in...Ch. 5.1 - Pets The diagram below shows the arrangement of a...Ch. 5.1 - Transportation A subway map is shown below. Is it...Ch. 5.1 - Prob. 29ESCh. 5.1 - Prob. 30ESCh. 5.1 - Degrees of Separation In the graph below, an edge...Ch. 5.1 - Social Network In the graph below, an edge...Ch. 5.1 - Prob. 33ESCh. 5.1 - Travel A map of South America is shown at the...Ch. 5.2 - Continue investigating Hamiltonian circuits in...Ch. 5.2 - Use the greedy algorithm and the weighted graph...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Transportation For the train routes given in...Ch. 5.2 - Transportation For the direct air flights given in...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Travel A company representative lives in...Ch. 5.2 - Travel A tourist is staying in Toronto, Canada,...Ch. 5.2 - Travel Use the edge-picking algorithm to design a...Ch. 5.2 - Travel Use the edge-picking algorithm to design a...Ch. 5.2 - Travel Nicole wants to tour Asia. She will start...Ch. 5.2 - Travel The prices for traveling between five...Ch. 5.2 - Travel Use the edge-picking algorithm to find a...Ch. 5.2 - Travel Use the edge-picking algorithm to find a...Ch. 5.2 - Route Planning Brian needs to visit the pet store,...Ch. 5.2 - Route Planning A bike messenger needs to deliver...Ch. 5.2 - Scheduling A research company has a large...Ch. 5.2 - Computer Networks A small office wishes to network...Ch. 5.2 - Route Planning A security officer patrolling a...Ch. 5.2 - Route Planning A city engineer needs to inspect...Ch. 5.2 - Draw a connected graph with six vertices that has...Ch. 5.2 - Assign weights to the edges of the following...Ch. 5.3 - The tetrahedron in figure 5.20 consists of four...Ch. 5.3 - The following graph is the projection of one ofthe...Ch. 5.3 - Prob. 3EECh. 5.3 - Give a reason why the graph below Cannot be the...Ch. 5.3 - Prob. 1ESCh. 5.3 - Prob. 2ESCh. 5.3 - Prob. 3ESCh. 5.3 - Prob. 4ESCh. 5.3 - Prob. 5ESCh. 5.3 - Prob. 6ESCh. 5.3 - Prob. 7ESCh. 5.3 - Prob. 8ESCh. 5.3 - Prob. 9ESCh. 5.3 - Prob. 10ESCh. 5.3 - Prob. 11ESCh. 5.3 - Prob. 12ESCh. 5.3 - Show that the following graph contracts to K5.Ch. 5.3 - Show that the following graph contracts to the...Ch. 5.3 - Prob. 15ESCh. 5.3 - Prob. 16ESCh. 5.3 - Prob. 17ESCh. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Prob. 23ESCh. 5.3 - Prob. 24ESCh. 5.3 - Prob. 25ESCh. 5.3 - Prob. 26ESCh. 5.3 - Prob. 27ESCh. 5.3 - Prob. 28ESCh. 5.3 - Prob. 29ESCh. 5.3 - Prob. 30ESCh. 5.4 - A one-way road ends at a two-way street. The...Ch. 5.4 - A one-way road intersects a two-way road in a...Ch. 5.4 - A two-way road intersects another two-way road in...Ch. 5.4 - Prob. 1ESCh. 5.4 - Prob. 2ESCh. 5.4 - Prob. 3ESCh. 5.4 - Prob. 4ESCh. 5.4 - Prob. 5ESCh. 5.4 - Prob. 6ESCh. 5.4 - Prob. 7ESCh. 5.4 - Prob. 8ESCh. 5.4 - Prob. 9ESCh. 5.4 - Prob. 10ESCh. 5.4 - Prob. 11ESCh. 5.4 - Prob. 12ESCh. 5.4 - Prob. 13ESCh. 5.4 - Prob. 14ESCh. 5.4 - Prob. 15ESCh. 5.4 - Prob. 16ESCh. 5.4 - Prob. 17ESCh. 5.4 - Prob. 18ESCh. 5.4 - Prob. 19ESCh. 5.4 - Prob. 20ESCh. 5.4 - Prob. 21ESCh. 5.4 - Prob. 22ESCh. 5.4 - Scheduling Six different groups of children would...Ch. 5.4 - Scheduling Five different charity organizations...Ch. 5.4 - Scheduling Students in a film class have...Ch. 5.4 - Animal Housing A researcher has discovered six new...Ch. 5.4 - Prob. 27ESCh. 5.4 - Prob. 28ESCh. 5.4 - Prob. 29ESCh. 5.4 - Prob. 30ESCh. 5.4 - Scheduling Edge colorings, as explained in...Ch. 5 - (a) determine the number of edges in the graph,...Ch. 5 - (a) determine the number of edges in the graph,...Ch. 5 - Soccer In the table below, an X indicates teams...Ch. 5 - Each vertex in the graph at the left represents a...Ch. 5 - Determine whether the two graphs are equivalent.Ch. 5 - Determine whether the two graphs are equivalent.Ch. 5 - Find an Euler path if possible, and (b) find an...Ch. 5 - Find an Euler path if possible, and (b) find an...Ch. 5 - Find an Euler path if possible, and (b) find an...Ch. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Architecture The floor plan of a sculpture gallery...Ch. 5 - Use Dirac's theorem to verify that the graph is...Ch. 5 - Use Dirac's theorem to verify that the graph is...Ch. 5 - Prob. 15RECh. 5 - Prob. 16RECh. 5 - Use the greedy algorithm to find a Hamiltonian...Ch. 5 - Use the greedy algorithm to find a Hamiltonian...Ch. 5 - Use the edge-picking algorithm to find a...Ch. 5 - Use the edge-picking algorithm to find a...Ch. 5 - Efficient Route The distances, in miles, between...Ch. 5 - Computer Networking A small office needs to...Ch. 5 - Prob. 23RECh. 5 - Prob. 24RECh. 5 - Prob. 25RECh. 5 - Prob. 26RECh. 5 - Count the number of vertices, edges, and faces in...Ch. 5 - Count the number of vertices, edges, and faces in...Ch. 5 - Prob. 29RECh. 5 - Prob. 30RECh. 5 - Prob. 31RECh. 5 - Prob. 32RECh. 5 - Prob. 33RECh. 5 - Prob. 34RECh. 5 - Scheduling A company has scheduled a retreat at a...Ch. 5 - Social Network Each vertex in the graph at the...Ch. 5 - Determine whether the following two graphs are...Ch. 5 - Answer the following questions for the graph shown...Ch. 5 - Recreation The illustration below depicts bridges...Ch. 5 - a. What does Dirac's theorem state? Explain how it...Ch. 5 - Low-Cost Route The table below shows the cost of...Ch. 5 - Use the greedy algorithm to find a Hamiltonian...Ch. 5 - Prob. 8TCh. 5 - Answer the following questions for the graph shown...Ch. 5 - Prob. 10TCh. 5 - Prob. 11TCh. 5 - A group of eight friends is planning a vacation in...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- What operations can be performed on a linear system to arrive at an equivalent system?arrow_forwardThree components are connected to form a system as shown in the accompanying diagram. Because the components in the 2-3 subsystem are connected in parallel, that subsystem will function if at least one of the two individual components functions. For the entire system to function, component 1 must function and so must the 2-3 subsystem. 2 The experiment consists of determining the condition of each component [S (success) for a functioning component and F (failure) for a nonfunctioning component]. (Enter your answers in set notation. Enter EMPTY or ø for the empty set.) (a) Which outcomes are contained in the event A that exactly two of the three components function? А — (b) Which outcomes are contained in the event B that at least two of the components function? B = (c) Which outcomes are contained in the event C that the system functions? C = (d) List outcomes in C'. C' = List outcomes in A u C. AUC = List outcomes in A n C. A n C = List outcomes in Bu C. BuC = List outcomes in B n C.…arrow_forwardFor a parallel structure of identical components, the system can succeed if at least one of the components succeeds. Assume that components fail independently of each other and that each component has a 0.09 probability of failure. Complete parts (a) through (c) below. T.... (a) Would it be unusual to observe one component fail? Two components? be unusual to observe one component fail, since the probability that one component fails, than 0.05. It be unusual to observe two components fail, since the probability that two components fail,, is than 0.05. (Type integers or decimals. Do not round.) (b) What is the probability that a parallel structure with 2 identical components will succeed? (Round to four decimal places as needed.) (c) How many components would be needed in the structure so that the probability the system will succeed is greater than 0.9998? (Type a whole number.) O Time Remaining: 02:29:14 Next Left Rahtarrow_forward
- Can you show that Q is an intensity matrix?arrow_forwardThree components are connected to form a system as shown in the accompanying diagram. Because the components in the 2–3 subsystem are connected in parallel, that subsystem will function if at least one of the two individual components functions. For the entire system to function, component 1 must function and so must the 2–3 subsystem. The experiment consists of determining the condition of each component [S (success) for a functioning component and F (failure) for a nonfunctioning component]. (Enter your answers in set notation. Enter EMPTY or ∅ for the empty set.) There us a graph shown in the pictures. Questions are posted on the pictures too.arrow_forwardA metallurgist is designing an experiment to determine the effect of flux, base metal, and energy input on the hardness of a weld. She wants to study four different fluxes, two different base metals, and three different amounts of energy input. If each run of the experiment involves a choice of one flux, one base metal, and one amount of energy input, how many different runs are possible?arrow_forward
- Three components are connected to form a system asshown in the accompanying diagram. Because the componentsin the 2–3 subsystem are connected in parallel, thatsubsystem will function if at least one of the two individualcomponents functions. For the entire system to function,component 1 must function and so must the 2–3 subsystem. The experiment consists of determining the condition ofeach component [S (success) for a functioning componentand F (failure) for a nonfunctioning component].a. Which outcomes are contained in the event A thatexactly two out of the three components function?b. Which outcomes are contained in the event B that atleast two of the components function?c. Which outcomes are contained in the event C that thesystem functions?d. List outcomes in C9, A ø C, A ù C, B ø C, andB ù C.arrow_forwardFor a parallel structure of identical components, the system can succeed if at least one of the components succeeds. Assume that components fail independently of each other and that each component has a 0.09 probability of failure, Complete parts (a) through (c) below. ..... (a) Would it be unusual to observe one component fail? Two components? be unusual to observe one component fail, since the probability that one component fails, is than 0.05. It be unusual to observe two components fail, since the probability that two components fail, than 0.05. (Type integers or decimals. Do not round.) (b) What is the probability that a parallel structure with 2 identical components will succeed? (Round to four decimal places as needed.) (c) How many components would be needed in the structure so that the probability the system will succe is greater than 0.9998? (Type a whole number.) 02 C4 888 Left Rahi S B. Control CommaRnd uondo uondarrow_forwardA product is processed on a station S1, which produces 75% good units, while remaining P1= 25% are sent to a rework station R1. At rework station, P2=10% are scrapped and the good parts are sent back to station S1. Draw the cycling production flow system and determine the total number of units that should be processed in the system to get 1000 good units at the 4 - end. a) 1144 b) 1094 c) 1114 d) 1084 e) 1034arrow_forward
- Consider an airport where taxis and customersarrive (exponential interarrival times) with respective rates of one and two per minute. No matter howmany other taxis are present, a taxi will wait. If anarriving customer does not find a taxi, the customerimmediately leaves.a. Model this system as an MyMy1 queue. (Hint:Think of the taxis as the “customers.”)b. Find the average number of taxis that are waitingfor a customer.c. Suppose all customers who use a taxi pay a$10 fare. During a typical hour, how much revenuewill the taxis receive?arrow_forwardQ2) if pCB) = PCP) =PCc)= 80%, PCA) = 85% ,PCE)= 90%. Find the reliability of the System. B. HAarrow_forwardFor a parallel structure of identical components, the system can succeed if at least one of the components succeeds. Assume that components fail independently of each other and that each component has a 0.22 probability of failure. Complete parts (a) through (c) below. ..... (a) Would it be unusual to observe one component fail? Two components? It be unusual to observe one component fail, since the probability that one component fails,, is than 0.05. It be unusual to observe two components fail, since the probability that two components fail, , is than 0.05. (Type integers or decimals. Do not round.) (b) What is the probability that a parallel structure with 2 identical components will succeed? (Round to four decimal places as needed.) (c) How many components would be needed in the structure so that the probability the system will succeed is greater than 0.9999? (Type a whole number.) DEC 16 étv J 280 MacBook Air 80 DII F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 公8arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning

College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY