Mathematical Excursions (MindTap Course List)
4th Edition
ISBN: 9781305965584
Author: Richard N. Aufmann, Joanne Lockwood, Richard D. Nation, Daniel K. Clegg
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5.1, Problem 34ES
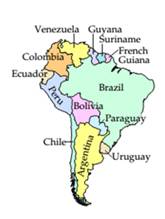
Travel A map of South America is shown at the left.
- Draw a graph in which the vertices represent the 13 countries of South America and two vertices are joined by an edge if the corresponding countries share a common border.
- Two friends are planning a driving tour of South America. They would like to drive across every border on the continent. Is it possible to plan such a route that never crosses the same border twice? What would the route correspond to on the graph?
- Find a route the friends can follow that will start and end in Venezuela and that Crosses every border while recrossing the fewest borders possible. Hint: On the graph, add multiple edges corresponding to border crossings that allow an Euler circuit.
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
21. ANALYSIS OF LAST DIGITS Heights of statistics students were obtained by the author as
part of an experiment conducted for class. The last digits of those heights are listed below.
Construct a frequency distribution with 10 classes. Based on the distribution, do the
heights appear to be reported or actually measured? Does there appear to be a gap in the
frequencies and, if so, how might that gap be explained? What do you know about the
accuracy of the results?
3 4
555
0 0 0 0 0 0 0 0 0 1 1 23 3
5 5 5 5 5 5 5 5 5 5 5 5 6 6 8 8 8 9
A side view of a recycling bin lid is diagramed below where two panels come together at a right angle.
45 in
24 in
Width? —
Given this information, how wide is the recycling bin in inches?
f'(x)
Chapter 5 Solutions
Mathematical Excursions (MindTap Course List)
Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - Explain why the following pen-tracing puzzle is...Ch. 5.1 - Transportation An X in the table below indicates a...Ch. 5.1 - Transportation The table below shows the nonstop...Ch. 5.1 - Social Network A group of friends is represented...Ch. 5.1 - Prob. 4ESCh. 5.1 - Determine (a) the number of edges in the graph,...
Ch. 5.1 - Determine (a) the number of edges in the graph,...Ch. 5.1 - Determine (a) the number of edges in the graph,...Ch. 5.1 - Determine (a) the number of edges in the graph,...Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Explain why the following two graphs cannot be...Ch. 5.1 - Label the vertices of the second graph so that it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - Parks in Exercises 23 and 24, a map of a park is...Ch. 5.1 - Parks in Exercises 23 and 24, a map of a park is...Ch. 5.1 - Transportation For the train routes given in...Ch. 5.1 - Transportation For the direct air flights given in...Ch. 5.1 - Pets The diagram below shows the arrangement of a...Ch. 5.1 - Transportation A subway map is shown below. Is it...Ch. 5.1 - Prob. 29ESCh. 5.1 - Prob. 30ESCh. 5.1 - Degrees of Separation In the graph below, an edge...Ch. 5.1 - Social Network In the graph below, an edge...Ch. 5.1 - Prob. 33ESCh. 5.1 - Travel A map of South America is shown at the...Ch. 5.2 - Continue investigating Hamiltonian circuits in...Ch. 5.2 - Use the greedy algorithm and the weighted graph...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Transportation For the train routes given in...Ch. 5.2 - Transportation For the direct air flights given in...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Travel A company representative lives in...Ch. 5.2 - Travel A tourist is staying in Toronto, Canada,...Ch. 5.2 - Travel Use the edge-picking algorithm to design a...Ch. 5.2 - Travel Use the edge-picking algorithm to design a...Ch. 5.2 - Travel Nicole wants to tour Asia. She will start...Ch. 5.2 - Travel The prices for traveling between five...Ch. 5.2 - Travel Use the edge-picking algorithm to find a...Ch. 5.2 - Travel Use the edge-picking algorithm to find a...Ch. 5.2 - Route Planning Brian needs to visit the pet store,...Ch. 5.2 - Route Planning A bike messenger needs to deliver...Ch. 5.2 - Scheduling A research company has a large...Ch. 5.2 - Computer Networks A small office wishes to network...Ch. 5.2 - Route Planning A security officer patrolling a...Ch. 5.2 - Route Planning A city engineer needs to inspect...Ch. 5.2 - Draw a connected graph with six vertices that has...Ch. 5.2 - Assign weights to the edges of the following...Ch. 5.3 - The tetrahedron in figure 5.20 consists of four...Ch. 5.3 - The following graph is the projection of one ofthe...Ch. 5.3 - Prob. 3EECh. 5.3 - Give a reason why the graph below Cannot be the...Ch. 5.3 - Prob. 1ESCh. 5.3 - Prob. 2ESCh. 5.3 - Prob. 3ESCh. 5.3 - Prob. 4ESCh. 5.3 - Prob. 5ESCh. 5.3 - Prob. 6ESCh. 5.3 - Prob. 7ESCh. 5.3 - Prob. 8ESCh. 5.3 - Prob. 9ESCh. 5.3 - Prob. 10ESCh. 5.3 - Prob. 11ESCh. 5.3 - Prob. 12ESCh. 5.3 - Show that the following graph contracts to K5.Ch. 5.3 - Show that the following graph contracts to the...Ch. 5.3 - Prob. 15ESCh. 5.3 - Prob. 16ESCh. 5.3 - Prob. 17ESCh. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Prob. 23ESCh. 5.3 - Prob. 24ESCh. 5.3 - Prob. 25ESCh. 5.3 - Prob. 26ESCh. 5.3 - Prob. 27ESCh. 5.3 - Prob. 28ESCh. 5.3 - Prob. 29ESCh. 5.3 - Prob. 30ESCh. 5.4 - A one-way road ends at a two-way street. The...Ch. 5.4 - A one-way road intersects a two-way road in a...Ch. 5.4 - A two-way road intersects another two-way road in...Ch. 5.4 - Prob. 1ESCh. 5.4 - Prob. 2ESCh. 5.4 - Prob. 3ESCh. 5.4 - Prob. 4ESCh. 5.4 - Prob. 5ESCh. 5.4 - Prob. 6ESCh. 5.4 - Prob. 7ESCh. 5.4 - Prob. 8ESCh. 5.4 - Prob. 9ESCh. 5.4 - Prob. 10ESCh. 5.4 - Prob. 11ESCh. 5.4 - Prob. 12ESCh. 5.4 - Prob. 13ESCh. 5.4 - Prob. 14ESCh. 5.4 - Prob. 15ESCh. 5.4 - Prob. 16ESCh. 5.4 - Prob. 17ESCh. 5.4 - Prob. 18ESCh. 5.4 - Prob. 19ESCh. 5.4 - Prob. 20ESCh. 5.4 - Prob. 21ESCh. 5.4 - Prob. 22ESCh. 5.4 - Scheduling Six different groups of children would...Ch. 5.4 - Scheduling Five different charity organizations...Ch. 5.4 - Scheduling Students in a film class have...Ch. 5.4 - Animal Housing A researcher has discovered six new...Ch. 5.4 - Prob. 27ESCh. 5.4 - Prob. 28ESCh. 5.4 - Prob. 29ESCh. 5.4 - Prob. 30ESCh. 5.4 - Scheduling Edge colorings, as explained in...Ch. 5 - (a) determine the number of edges in the graph,...Ch. 5 - (a) determine the number of edges in the graph,...Ch. 5 - Soccer In the table below, an X indicates teams...Ch. 5 - Each vertex in the graph at the left represents a...Ch. 5 - Determine whether the two graphs are equivalent.Ch. 5 - Determine whether the two graphs are equivalent.Ch. 5 - Find an Euler path if possible, and (b) find an...Ch. 5 - Find an Euler path if possible, and (b) find an...Ch. 5 - Find an Euler path if possible, and (b) find an...Ch. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Architecture The floor plan of a sculpture gallery...Ch. 5 - Use Dirac's theorem to verify that the graph is...Ch. 5 - Use Dirac's theorem to verify that the graph is...Ch. 5 - Prob. 15RECh. 5 - Prob. 16RECh. 5 - Use the greedy algorithm to find a Hamiltonian...Ch. 5 - Use the greedy algorithm to find a Hamiltonian...Ch. 5 - Use the edge-picking algorithm to find a...Ch. 5 - Use the edge-picking algorithm to find a...Ch. 5 - Efficient Route The distances, in miles, between...Ch. 5 - Computer Networking A small office needs to...Ch. 5 - Prob. 23RECh. 5 - Prob. 24RECh. 5 - Prob. 25RECh. 5 - Prob. 26RECh. 5 - Count the number of vertices, edges, and faces in...Ch. 5 - Count the number of vertices, edges, and faces in...Ch. 5 - Prob. 29RECh. 5 - Prob. 30RECh. 5 - Prob. 31RECh. 5 - Prob. 32RECh. 5 - Prob. 33RECh. 5 - Prob. 34RECh. 5 - Scheduling A company has scheduled a retreat at a...Ch. 5 - Social Network Each vertex in the graph at the...Ch. 5 - Determine whether the following two graphs are...Ch. 5 - Answer the following questions for the graph shown...Ch. 5 - Recreation The illustration below depicts bridges...Ch. 5 - a. What does Dirac's theorem state? Explain how it...Ch. 5 - Low-Cost Route The table below shows the cost of...Ch. 5 - Use the greedy algorithm to find a Hamiltonian...Ch. 5 - Prob. 8TCh. 5 - Answer the following questions for the graph shown...Ch. 5 - Prob. 10TCh. 5 - Prob. 11TCh. 5 - A group of eight friends is planning a vacation in...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- If you are using chatgpt leave it I will downvote .arrow_forwardTemperature measurements are based on the transfer of heat between the sensor of a measuring device (such as an ordinary thermometer or the gasket of a thermocouple) and the medium whose temperature is to be measured. Once the sensor or thermometer is brought into contact with the medium, the sensor quickly receives (or loses, if warmer) heat and reaches thermal equilibrium with the medium. At that point the medium and the sensor are at the same temperature. The time required for thermal equilibrium to be established can vary from a fraction of a second to several minutes. Due to its small size and high conductivity it can be assumed that the sensor is at a uniform temperature at all times, and Newton's cooling law is applicable. Thermocouples are commonly used to measure the temperature of gas streams. The characteristics of the thermocouple junction and the gas stream are such that λ = hA/mc 0.02s-1. Initially, the thermocouple junction is at a temperature Ti and the gas stream at…arrow_forwardA body of mass m at the top of a 100 m high tower is thrown vertically upward with an initial velocity of 10 m/s. Assume that the air resistance FD acting on the body is proportional to the velocity V, so that FD=kV. Taking g = 9.75 m/s2 and k/m = 5 s, determine: a) what height the body will reach at the top of the tower, b) how long it will take the body to touch the ground, and c) the velocity of the body when it touches the ground.arrow_forward
- A chemical reaction involving the interaction of two substances A and B to form a new compound X is called a second order reaction. In such cases it is observed that the rate of reaction (or the rate at which the new compound is formed) is proportional to the product of the remaining amounts of the two original substances. If a molecule of A and a molecule of B combine to form a molecule of X (i.e., the reaction equation is A + B ⮕ X), then the differential equation describing this specific reaction can be expressed as: dx/dt = k(a-x)(b-x) where k is a positive constant, a and b are the initial concentrations of the reactants A and B, respectively, and x(t) is the concentration of the new compound at any time t. Assuming that no amount of compound X is present at the start, obtain a relationship for x(t). What happens when t ⮕∞?arrow_forwardConsider a body of mass m dropped from rest at t = 0. The body falls under the influence of gravity, and the air resistance FD opposing the motion is assumed to be proportional to the square of the velocity, so that FD = kV2. Call x the vertical distance and take the positive direction of the x-axis downward, with origin at the initial position of the body. Obtain relationships for the velocity and position of the body as a function of time t.arrow_forwardAssuming that the rate of change of the price P of a certain commodity is proportional to the difference between demand D and supply S at any time t, the differential equations describing the price fluctuations with respect to time can be expressed as: dP/dt = k(D - s) where k is the proportionality constant whose value depends on the specific commodity. Solve the above differential equation by expressing supply and demand as simply linear functions of price in the form S = aP - b and D = e - fParrow_forward
- Find the area of the surface obtained by rotating the circle x² + y² = r² about the line y = r.arrow_forward3) Recall that the power set of a set A is the set of all subsets of A: PA = {S: SC A}. Prove the following proposition. АСВ РАСРВarrow_forwardA sequence X = (xn) is said to be a contractive sequence if there is a constant 0 < C < 1 so that for all n = N. - |Xn+1 − xn| ≤ C|Xn — Xn−1| -arrow_forward
- 3) Find the surface area of z -1≤ y ≤1 = 1 + x + y + x2 over the rectangle −2 ≤ x ≤ 1 and - Solution: TYPE YOUR SOLUTION HERE! ALSO: Generate a plot of the surface in Mathematica and include that plot in your solution!arrow_forward7. Walkabout. Does this graph have an Euler circuit? If so, find one. If not, explain why not.arrow_forwardBelow, let A, B, and C be sets. 1) Prove (AUB) nC = (ANC) U (BNC).arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY