
5.43 and 5.44
Determine by direct integration the centroid of the area shown. Express your answer in terms of a and b.
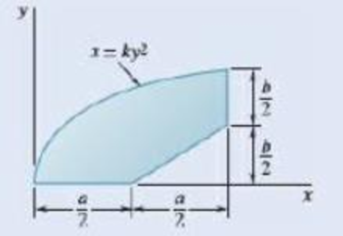
Fig. P5.43
The centroid of shaded area in Fig. P5.43 by method of direct integration.
Answer to Problem 5.43P
Centroid is located at
Explanation of Solution
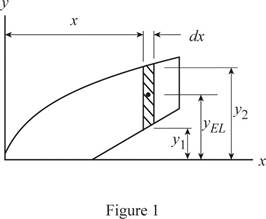
Refer the figure P5.43 and figure given below.
Write the equation for curve
Here,
Consider the point
Here,
Rewrite equation (I) by substituting
Rewrite the above equation in terms of
Rewrite equation (I) by substituting the above relation for
Rewrite the above equation in terms of
Divide the shaded region in P5.43 into two parts for the purpose of integration. Region
Consider the region
Consider a rectangular differential area element in the region. Write the expression for the x-coordinate of center of mass of differential area element.
Here,
Write the expression for the y-coordinate of center of mass of differential area element in region
Here,
Rewrite the above relation by substituting
Write the expression to calculate the differential area element in
Here,
Rewrite the above relation by substituting
Consider the region
Write the expression for the x-coordinate of center of mass of differential area element in region
Here,
Write the expression for the y-coordinate of center of mass of differential area element in region
Here,
Calculate the slope of
Here,
Write the equation of
Rewrite the above equation by substituting
Rewrite equation (IV) by substituting the above relation for
Write the expression for
Rewrite the above relation by substituting
Write the equation to calculate the total area of shaded region in P5.43.
Here,
Rewrite the above equation by substituting equation (III) and (V).
Write the expression for
Rewrite the above equation by substituting equation (III) and (V).
Write the expression for
Rewrite the above equation by substituting equations (II), (III), (V) and (VI).
Write the expression for first moment of whole area about y-axis.
Here,
Rewrite the above relation by substituting
Rewrite the above relation in terms of
Write the expression for first moment of whole area about x-axis.
Here,
Rewrite the above relation in terms of
Therefore, the centroid is located at
Want to see more full solutions like this?
Chapter 5 Solutions
Connect 1 Semester Access Card for Vector Mechanics for Engineers: Statics and Dynamics
- The members of a truss are connected to the gusset plate as shown in (Figure 1). The forces are concurrent at point O. Take = 90° and T₁ = 7.5 kN. Part A Determine the magnitude of F for equilibrium. Express your answer to three significant figures and include the appropriate units. F= 7.03 Submit ? kN Previous Answers Request Answer × Incorrect; Try Again; 21 attempts remaining ▾ Part B Determine the magnitude of T2 for equilibrium. Express your answer to three significant figures and include the appropriate units. Figure T₂ = 7.03 C T2 |? KN Submit Previous Answers Request Answer × Incorrect; Try Again; 23 attempts remaining Provide Feedbackarrow_forwardConsider the following acid-base reaction: Fe3+(aq) +3H2O -Fe(OH)3 (s) + 3H* ← A. Using thermodynamics, calculate the equilibrium constant K at 25°C (The AG° of formation of Fe(OH)3(s) is -699 kJ/mol). B. Using the value of K you calculated in part a, if a solution contains 10-4 M Fe3+ and has a pH of 7.5, will Fe(OH)3(s) precipitate? Show all calculations necessary to justify your answer. Note that the reaction as written is for precipitation, not dissolution like Ksp-arrow_forwardA vertical force of F = 3.4 kN is applied to the hook at A as shown in. Set d = 1 m. Part A 3 m 3m 0.75 m 1.5 m. Determine the tension in cable AB for equilibrium. Express your answer to three significant figures and include the appropriate units. FAB= Value Submit Request Answer Part B Units ? Determine the tension in cable AC for equilibrium. Express your answer to three significant figures and include the appropriate units. FAC = Value Submit Request Answer Part C ? Units Determine the tension in cable AD for equilibrium. Express your answer to three significant figures and include the appropriate units.arrow_forward
- Consider the heat engine operating at steady state between the two thermal reservoirs shown at the right while producing a net power output of 700 kW. If 1000 kW of heat (Q̇H) is transferred to the heat engine from a thermal reservoir at a temperature of TH = 900 K, and heat is rejected to a thermal reservoir at a temperature of TL = 300 K, is this heat engine possible? Can you answer this question for me and show all of the workarrow_forward1.12 A disk of constant radius r is attached to a telescoping rod that is extending at a constant rate as shown in Fig. P1.12. Both the disk and the rod are rotating at a constant rate. Find the inertial velocity and acceleration of point P at the rim of the disk. ท2 L 0 SS P α e 0 O' êL Fig. P1.12 Rotating disk attached to telescoping rod. 60 LLarrow_forwardTwo different options A and B with brake pads for disc brakes are connected to the rope drum. The diameter of the rope drum is 150 mm. What distance must the pads B be at from the center of rotation to cover the same distance as A?A B- Width 50 mm - Width 60 mm- Evidence center 120mm - Construction power 900 N from rotation center.- Maintains a weight of 200 kgwhen the installation force is 1.4kN (μ is missing from the data)M=μF(Ry-Ri)Right answer R=187 mmarrow_forward
- Assume the xy plane is level ground, and that the vertical pole shown in the diagram lies along the z-axis with its base at the origin. If the pole is 5 m tall, and a rope is used to pull on the top of the pole with a force of 400 N as shown, determine the magnitudes of the parallel and perpendicular components of the force vector with respect to the axis of the post i.e. with respect to the z-axis.arrow_forward4-1 Q4: Q5: (20 Marks) Find √48 using False Position Method with three iterations. Hint: the root lies between 3 and 4. (20 Marks)arrow_forwardDetermine the angle between vectors FA and FB that is less than 180 degrees. FA is the vector drawn from the origin to point A (-4, 4, 2) while FB is the vector drawn from the origin to point B (3, 1, -3).arrow_forward
- Find the resultant force vector from adding F1, F2 and F3, where … F1 = {-8i+10j-32k} N F2 is 40 N in magnitude with coordinate direction angles α, β, and γ, of 45, 120 and 60 degrees, respectively and F3 is 22 N in magnitude with transverse and azimuth angles of 65 and 40 degrees, respectively Express your final answer as a Cartesian vector as well as a magnitude with angles.arrow_forwardA 2-kW resistance heater wire with thermal conductivity of k=20 W/mK, a diameter of D=4mm, and a length of L=0.9m is used to boil water. If the outer surface temp of the resistance wire is Ts=110 degrees C, determine the temp at the center of the wire.arrow_forwardA flat-plate solar collector is used to heat water by having water flow through tubes attached at the back of the thin solar absorber plate. The absorber plate has emmisssivity and an absorptivity of 0.9. The top surface where x=0 temp of the absorber is T0=35 degrees C, and solar radiation is incident on the basorber at 500 W/m^2 with a surrounding temp of 0 degrees C. The convection heat transfer coefficient at the absorber surface is 5 W/m^2 K, while the ambient temp is 25 degrees C. Show that the variation of the temp in the basorber plate can be expressed as T(x)=-(q0/k)x+T0, and determine net heat flux, q, absorbed by solar collector.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





