
Locate the centroid of the section shown, which was cut f a thin circular pipe by two oblique planes.
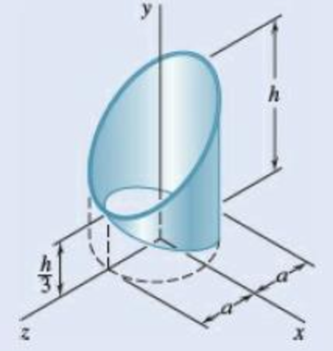
Fig. P5.133
(a)
The location of the centre of gravity of the bowl.
Answer to Problem 5.133P
The location of the centre of gravity of the bowl is
Explanation of Solution
Refer Fig. P5.132 and Fig. 1.
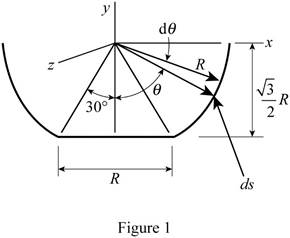
For the coordinate axis given below, using the symmetry of the diagram, determine the x and z coordinates of the centre of gravity.
The bowl can be assumed as a shell, where the centre of gravity coincides with the centroid of the shell.
The element of area is obtained by rotating the arc ds about the y-axis for the walls of the bowl.
Write the expression for the area of the element.
Here,
Write the expression for y coordinate of the centroid of the element.
Here,
Write the expression for
Write the expression for y coordinate of the centre of gravity.
Here,
Conclusion:
Calculate the area using equation (I).
Substitute (I) and (II) in (III).
From figure 1, find the area of the base and distance of the centroid of the base to the y axis.
Substitute equations (V), (VI) and (VII) in equation (IV).
Substitute
Therefore, the location of the centre of gravity of the bowl is
(b)
The location of the centre of gravity of the punch.
Answer to Problem 5.133P
The location of the centre of gravity of the bowl is
Explanation of Solution
Refer Fig. P5.132 and Fig. 2.
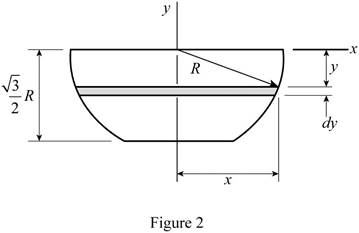
For the coordinate axis given below, using the symmetry of the diagram, determine the x and z coordinates of the centre of gravity.
The punch can be assumed as homogenous, where the centre of gravity coincides with the centroid of the volume.
The element of volume of the disk has radius x and thickness dy.
Find the expression for
Write the expression for the volume of the element.
Here,
Write the expression for y coordinate of the centre of gravity.
Conclusion:
Calculate the volume using equation (IX).
Find
Substitute equations (XI), and (XII) in equation (X).
Substitute
Therefore, the location of the centre of gravity of the bowl is
Want to see more full solutions like this?
Chapter 5 Solutions
Connect 1 Semester Access Card for Vector Mechanics for Engineers: Statics and Dynamics
- Example find f(t)? -4s F(s)= (s² + 4)²arrow_forwarddraw a kinematic diagramarrow_forwardRigid bodies ENG2016. Full complete solutions need okk don't use guidelines but solve full accurate steps by steps don't use chat gpt or any other ai okkk just solve complete solutions okkk take your time but solve complete solutionsarrow_forward
- Question 6 I need to show all work step by step dynamicsarrow_forwardQu. 3 The automobile is originally at rest s = 0. If it then starts to increase its speed at i = (0.05t2)ft/s?, where t is in seconds, determine the magnitudes of its velocity and acceleration at s = 550 ft. please show all work from dynamics step by step formulaarrow_forwardquestion 5 and 6 from dynamics I need to show all work step by step problemsarrow_forward
- Study Area Document Sharing User Settings Access Pearson mylabmastering.pearson.com P Pearson MyLab and Mastering The crash cushion for a highway barrier consists of a nest of barrels filled with an impact-absorbing material. The barrier stopping force is measured versus the vehicle penetration into the barrier. (Figure 1) Part A P Course Home b My Questions | bartleby Review Determine the distance a car having a weight of 4000 lb will penetrate the barrier if it is originally traveling at 55 ft/s when it strikes the first barrel. Express your answer to three significant figures and include the appropriate units. Figure 1 of 1 36 μΑ S = Value Units Submit Request Answer Provide Feedback ? Next >arrow_forwardWater is the working fluid in an ideal Rankine cycle. Saturated vapor enters the turbine at 12 MPa, and the condenser pressure is 8 kPa. The mass flow rate of steam entering the turbine is 50 kg/s. Determine: (a) the net power developed, in kW. (b) the rate of heat transfer to the steam passing through the boiler, in kW. (c) the percent thermal efficiency. (d) the mass flow rate of condenser cooling water, in kg/s, if the cooling water undergoes a temperature increase of 18°C with negligible pressure change in passing through the condenser.arrow_forward4. The figure below shows a bent pipe with the external loading FA 228 lb, and M₁ = M₂ = 1 kip-ft. The force Fernal loading FA = 300 lb, FB: parallel to the y-axis, and and yc = 60°. = 125 lb, Fc = acts parallel to the x-z plane, the force FB acts Cartesian resultan Coordinate direction angles of Fc are ac = 120°, ẞc = 45°, a. Compute the resultant force vector of the given external loading and express it in EST form. b. Compute the resultant moment vector of the given external loading about the origin, O, and express it in Cartesian vector form. Use the vector method while computing the moments of forces. c. Compute the resultant moment vector of the given external loading about the line OA and express it in Cartesian vector form. :00 PM EST k ghoufran@buffaternal du 2 ft M₁ A 40° FA M2 C 18 in 1 ft Fc 25 houfran@bald.edu - Feb 19, 3 ft FBarrow_forward
- The differential equation of a cruise control system is provided by the following equation: Find the closed loop transfer function with respect to the reference velocity (vr) . a. Find the poles of the closed loop transfer function for different values of K. How does the poles move as you change K? b. Find the step response for different values of K and plot in MATLAB. What can you observe? c. For the given transfer function, find tp, ts, tr, Mp . Plot the resulting step response. G(s) = 40/(s^2 + 4s + 40)arrow_forwardAuto Controls Perform the partial fraction expansion of the following transfer function and find the impulse response: G(s) = (s/2 + 5/3) / (s^2 + 4s + 6) G(s) =( 6s^2 + 50) / (s+3)(s^2 +4)arrow_forwardStudy Area Document Sharing User Settings mylabmastering.pearson.com Access Pearson P Pearson MyLab and Mastering The 150-lb skater passes point A with a speed of 6 ft/s. (Figure 1) Figure 1 of 1 Part A P Course Home b My Questions | bartleby Determine his speed when he reaches point B. Neglect friction. Express your answer to three significant figures and include the appropriate units. με ? VB = Value Units Submit Request Answer Part B Determine the normal force exerted on him by the track at this point. Express your answer to three significant figures and include the appropriate units. ☐ о Α NB = Value Units Submit Request Answer Provide Feedback ? ■Review Next >arrow_forward
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
