Introductory Statistics (10th Edition)
10th Edition
ISBN: 9780321989178
Author: Neil A. Weiss
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5.2, Problem 37E
Archery. An archer shoots an arrow into a square target 6 feet on a side whose center we call the origin. The outcome of this random experiment is the point in the target hit by the arrow. The archer scores 10 points if she hits the bull’s eye—a disk of radius 1 foot centered at the origin; she scores 5 points if she hits the ring with inner radius 1 foot and outer radius 2 feet centered at the origin; and she scores 0 points otherwise. Assume that the archer will actually hit the target and is equally likely to hit any portion of the target. For one arrow shot, let S be the score. A probability distribution for the random variable S is as follows.
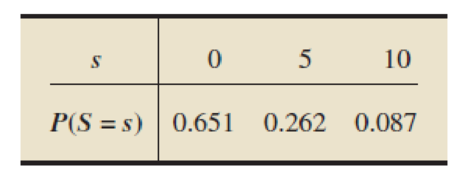
- a. On average, how many points will the archer score per arrow shot?
- b. Obtain and interpret the standard deviation of the score per arrow shot.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Cycles to
failure
Position in
ascending
order
0.5
f(x))
(x;)
Problem 44
Marsha, a renowned cake scientist, is trying to determine how long different cakes can survive intense fork attacks before collapsing into crumbs.
To simulate real-world cake consumption, she designs a test where cakes are subjected to repeated fork stabs and bites, mimicking the brutal
reality of birthday parties. After rigorous testing, Marsha records 10 observations of how many stabs each cake endured before structural failure.
Construct P-P plots for (a.) a normal distribution, (b.) a lognormal distribution, and (c.) a Weibull distribution (using the information included in the
table below). Which distribution seems to be the best model for the cycles to failure for this material? Explain your answer in detail.
Observation
Empirical
cumulative
Probability distribution
Cumulative distribution
Inverse of cumulative
distribution F-1 (-0.5)
F(x))
(S)
n
4
3
1
0.05
9
5
2
0.15
7
7
3
0.25
1
10
4
0.35
3
12
5
0.45
Normal…
Problem 3
In their lab, engineer Daniel and Paulina are desperately trying to perfect time travel. But the problem is that
their machine still struggles with power inconsistencies-sometimes generating too little energy, other times
too much, causing unstable time jumps. To prevent catastrophic misjumps into the Jurassic era or the far
future, they must calibrate the machine's power output. After extensive testing, they found that the time
machine's power output follows a normal distribution, with an average energy level of 8.7 gigawatts and a
standard deviation of 1.2 gigawatts.
The Time Travel Safety Board has set strict guidelines: For a successful time jump, the
machine's power must be between 8.5 and 9.5 gigawatts. What is the probability that a randomly
selected time jump meets this precision requirement?
Daniel suggests that adjusting the mean power output could improve time-travel accuracy.
Can adjusting the mean reduce the number of dangerous misjumps? If yes, what should the…
Problem 5 (
Marybeth is also interested in the experiment from Problem 2 (associated with the enhancements for Captain
America's shield), so she decides to start a detailed literature review on the subject. Among others, she found
a paper where they used a 2"(4-1) fractional factorial design in the factors: (A) shield material, (B) throwing
mechanism, (C) edge modification, and (D) handle adjustment. The experimental design used in the paper is
shown in the table below.
a.
Run
A
B
с
D
1
(1)
-1
-1
-1
1
2
a
1
-1
-1
1
3
bd
-1
1
-1
1
4
abd
1
1
-1
1
5
cd
-1
-1
1
-1
6
acd
1
-1
1
-1
7
bc
-1
1
1
-1
abc
1
1
1
-1
paper?
s) What was the generator used in the 2"(4-1) fractional factorial design described in the
b.
Based on the resolution of this design, what do you think about the generator used in the
paper? Do you think it was a good choice, or would you have selected a different one? Explain your
answer in detail.
Chapter 5 Solutions
Introductory Statistics (10th Edition)
Ch. 5.1 - Fill in the blanks. a. A relative-frequency...Ch. 5.1 - Provide an example (other than one discussed in...Ch. 5.1 - Let X denote the number of siblings of a randomly...Ch. 5.1 - Fill in the blank. For a discrete random variable,...Ch. 5.1 - Suppose that you make a large number of...Ch. 5.1 - What rule of probability permits you to obtain any...Ch. 5.1 - A variable x of a finite population has the...Ch. 5.1 - A variable y of a finite population has the...Ch. 5.1 - A variable y of a finite population has the...Ch. 5.1 - A variable x of a finite population has the...
Ch. 5.1 - Space Shuttles. The National Aeronautics and Space...Ch. 5.1 - Persons per Housing Unit. From the document...Ch. 5.1 - Major Hurricanes. The Atlantic Hurricane Database...Ch. 5.1 - Childrens Gender. A certain couple is equally...Ch. 5.1 - Dice. When two balanced dice are rolled, 36...Ch. 5.1 - World Series. The World Series in baseball is won...Ch. 5.1 - Archery. An archer shoots an arrow into a square...Ch. 5.1 - Solar Eclipses. The World Almanac provides...Ch. 5.1 - Black Bear Litters. In the article Reproductive...Ch. 5.1 - All-Numeric Passwords. The technology consultancy...Ch. 5.1 - Suppose that P(Z 1.96) = 0.025. Find P(Z 1.96)....Ch. 5.1 - Suppose that T and Z are random variables. a. If...Ch. 5.1 - Prob. 23ECh. 5.2 - What concept does the mean of a discrete random...Ch. 5.2 - Comparing Investments. Suppose that the random...Ch. 5.2 - In Exercises 5.275.30, we have provided the...Ch. 5.2 - In Exercises 5.275.30, we have provided the...Ch. 5.2 - In Exercises 5.275.30, we have provided the...Ch. 5.2 - In Exercises 5.275.30, we have provided the...Ch. 5.2 - In Exercises 5.315.35, we have provided the...Ch. 5.2 - In Exercises 5.315.35, we have provided the...Ch. 5.2 - In Exercises 5.315.35, we have provided the...Ch. 5.2 - In Exercises 5.315.35, we have provided the...Ch. 5.2 - In Exercises 5.315.35, we have provided the...Ch. 5.2 - World Series. The World Series in baseball is won...Ch. 5.2 - Archery. An archer shoots an arrow into a square...Ch. 5.2 - All-Numeric Passwords. The technology consultancy...Ch. 5.2 - Expected Value. As noted in Definition 5.4 on page...Ch. 5.2 - Evaluating Investments. An investor plans to put...Ch. 5.2 - Homeowners Policy. An insurance company wants to...Ch. 5.2 - Prob. 42ECh. 5.2 - Equipment Breakdowns. A factory manager collected...Ch. 5.2 - Simulation. Let X be the value of a randomly...Ch. 5.2 - Mean as Center of Gravity. Let X be a discrete...Ch. 5.2 - Equipment Breakdowns. Refer to Exercise 5.43....Ch. 5.2 - Equipment Breakdowns. The factory manager in...Ch. 5.3 - In probability and statistics, what is each...Ch. 5.3 - Under what three conditions are repeated trials of...Ch. 5.3 - Explain the significance of binomial coefficients...Ch. 5.3 - Discuss the pros and cons of binomial probability...Ch. 5.3 - What is the binomial distribution?Ch. 5.3 - Suppose that a simple random sample is taken from...Ch. 5.3 - Give two examples of Bernoulli trials other than...Ch. 5.3 - What does the bi in binomial signify?Ch. 5.3 - Compute 3!, 7!, 8!, and 9!.Ch. 5.3 - Find 1!, 2!, 4!, and 6!.Ch. 5.3 - Evaluate the following binomial coefficients. a....Ch. 5.3 - Evaluate the following binomial coefficients. a....Ch. 5.3 - Evaluate the following binomial coefficients. a....Ch. 5.3 - Determine the value of each binomial coefficient....Ch. 5.3 - For each of the following probability histograms...Ch. 5.3 - For each of the following probability histograms...Ch. 5.3 - Pinworm Infestation. Pinworm infestation, which is...Ch. 5.3 - Psychiatric Disorders. The National Institute of...Ch. 5.3 - In each of Exercises 5.675.72, we have provided...Ch. 5.3 - In each of Exercises 5.675.72, we have provided...Ch. 5.3 - In each of Exercises 5.675.72, we have provided...Ch. 5.3 - In each of Exercises 5.675.72, we have provided...Ch. 5.3 - In each of Exercises 5.675.72, we have provided...Ch. 5.3 - In each of Exercises 5.675.72, we have provided...Ch. 5.3 - Prob. 73ECh. 5.3 - Psychiatric Disorders. Use Procedure 5.1 on page...Ch. 5.3 - Tossing a Coin. If we repeatedly toss a balanced...Ch. 5.3 - Rolling a Die. If we repeatedly roll a balanced...Ch. 5.3 - Horse Racing. According to the Daily Racing Form,...Ch. 5.3 - Gestation Periods. The probability is 0.314 that...Ch. 5.3 - Traffic Fatalities and Intoxication. The National...Ch. 5.3 - Multiple-Choice Exams. A student takes a...Ch. 5.3 - Love Stinks? J. Fetto, in the article Love Stinks...Ch. 5.3 - Carbon Tax. A poll commissioned by Friends of the...Ch. 5.3 - Video Games. A pathological video game user (PVGU)...Ch. 5.3 - Recidivism. In the Scientific American article...Ch. 5.3 - Roulette. A success, s, in Bernoulli trials is...Ch. 5.3 - Sampling and the Binomial Distribution. Refer to...Ch. 5.3 - Sampling and the Binomial Distribution. Following...Ch. 5.3 - The Hypergeometric Distribution. In this exercise,...Ch. 5.3 - To illustrate, again consider the Mega Millions...Ch. 5.3 - To illustrate, consider the following problem:...Ch. 5.4 - Identify two uses of Poisson distributions.Ch. 5.4 - Why cant all the probabilities for a Poisson...Ch. 5.4 - For a Poisson random variable, what is the...Ch. 5.4 - What conditions should be satisfied in order to...Ch. 5.4 - Prob. 95ECh. 5.4 - Prob. 96ECh. 5.4 - In each of Exercises 5.965.99, we have provided...Ch. 5.4 - Prob. 98ECh. 5.4 - In each of Exercises 5.965.99, we have provided...Ch. 5.4 - Amusement Ride Safety. Approximately 297 million...Ch. 5.4 - Polonium. In the 1910 article The Probability...Ch. 5.4 - Wasps. M. Goodisman et al. studied patterns in...Ch. 5.4 - Wars. In the paper The Distribution of Wars in...Ch. 5.4 - Motel Reservations. M. Driscoll and N. Weiss...Ch. 5.4 - Cherry Pies. At one time, a well-known restaurant...Ch. 5.4 - Motor-Vehicle Deaths. According to Injury Facts, a...Ch. 5.4 - Prisoners. From the U.S. Census Bureau and the...Ch. 5.4 - The Challenger Disaster. In a letter to the editor...Ch. 5.4 - Fragile X Syndrome. The second-leading genetic...Ch. 5.4 - Holes in One. Refer to the case study on page 223....Ch. 5.4 - A Yellow Lobster! As reported by the Associated...Ch. 5.4 - With regard to the use of a Poisson distribution...Ch. 5.4 - Roughly speaking, you can use the Poisson...Ch. 5 - Fill in the blanks. a. A ______ is a quantitative...Ch. 5 - Prob. 2RPCh. 5 - Prob. 3RPCh. 5 - If you sum the probabilities of the possible...Ch. 5 - A random variable X equals 2 with probability...Ch. 5 - A random variable X has mean 3.6. If you make a...Ch. 5 - Prob. 7RPCh. 5 - Prob. 8RPCh. 5 - Prob. 9RPCh. 5 - List the three requirements for repeated trials of...Ch. 5 - What is the relationship between Bernoulli trials...Ch. 5 - In 10 Bernoulli trials, how many outcomes contain...Ch. 5 - Craps. The game of craps is played by rolling two...Ch. 5 - Following are two probability histograms of...Ch. 5 - Prob. 15RPCh. 5 - Prob. 16RPCh. 5 - ASU Enrollment Summary. According to the Arizona...Ch. 5 - Prob. 18RPCh. 5 - Busy Phone Lines. Refer to the probability...Ch. 5 - Craps. Use the binomial probability formula to...Ch. 5 - Penalty Kicks. In the game of soccer, a penalty...Ch. 5 - Pets. According to JAVMA News, a publication of...Ch. 5 - Pets. Refer to Problem 22. a. Draw a probability...Ch. 5 - Prob. 24RPCh. 5 - Prob. 25RPCh. 5 - Meteoroids. In the article Interstellar Pelting...Ch. 5 - Emphysema. The respiratory disease emphysema,...Ch. 5 - Prob. 28RPCh. 5 - As we reported at the beginning of this chapter,...
Additional Math Textbook Solutions
Find more solutions based on key concepts
1. How much money is Joe earning when he’s 30?
Pathways To Math Literacy (looseleaf)
1. How is a sample related to a population?
Elementary Statistics: Picturing the World (7th Edition)
Check Your Understanding
Reading Check Complete each sentence using > or < for □.
RC1. 3 dm □ 3 dam
Basic College Mathematics
For Problems 23-28, write in simpler form, as in Example 4. logbFG
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Empirical versus Theoretical A Monopoly player claims that the probability of getting a 4 when rolling a six-si...
Introductory Statistics
Reading, Writing, and Rounding Whole Numbers Write in words. 357
Mathematics for the Trades: A Guided Approach (11th Edition) (What's New in Trade Math)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- Suppose we wish to test the hypothesis that women with a sister’s history of breast cancer are at higher risk of developing breast cancer themselves. Suppose we assume that the prevalence rate of breast cancer is 3% among 60- to 64-year-old U.S. women, whereas it is 5% among women with a sister history. We propose to interview 400 women 40 to 64 years of age with a sister history of the disease. What is the power of such a study assuming that the level of significance is 10%? I only need help writing the null and alternative hypotheses.arrow_forward4.96 The breaking strengths for 1-foot-square samples of a particular synthetic fabric are approximately normally distributed with a mean of 2,250 pounds per square inch (psi) and a standard deviation of 10.2 psi. Find the probability of selecting a 1-foot-square sample of material at random that on testing would have a breaking strength in excess of 2,265 psi.4.97 Refer to Exercise 4.96. Suppose that a new synthetic fabric has been developed that may have a different mean breaking strength. A random sample of 15 1-foot sections is obtained, and each section is tested for breaking strength. If we assume that the population standard deviation for the new fabric is identical to that for the old fabric, describe the sampling distribution forybased on random samples of 15 1-foot sections of new fabricarrow_forwardUne Entreprise œuvrant dans le domaine du multividéo donne l'opportunité à ses programmeurs-analystes d'évaluer la performance des cadres supérieurs. Voici les résultats obtenues (sur une échelle de 10 à 50) où 50 représentent une excellente performance. 10 programmeurs furent sélectionnés au hazard pour évaluer deux cadres. Un rapport Excel est également fourni. Programmeurs Cadre A Cadre B 1 34 36 2 32 34 3 18 19 33 38 19 21 21 23 7 35 34 8 20 20 9 34 34 10 36 34 Test d'égalité des espérances: observations pairéesarrow_forward
- A television news channel samples 25 gas stations from its local area and uses the results to estimate the average gas price for the state. What’s wrong with its margin of error?arrow_forwardYou’re fed up with keeping Fido locked inside, so you conduct a mail survey to find out people’s opinions on the new dog barking ordinance in a certain city. Of the 10,000 people who receive surveys, 1,000 respond, and only 80 are in favor of it. You calculate the margin of error to be 1.2 percent. Explain why this reported margin of error is misleading.arrow_forwardYou find out that the dietary scale you use each day is off by a factor of 2 ounces (over — at least that’s what you say!). The margin of error for your scale was plus or minus 0.5 ounces before you found this out. What’s the margin of error now?arrow_forward
- Suppose that Sue and Bill each make a confidence interval out of the same data set, but Sue wants a confidence level of 80 percent compared to Bill’s 90 percent. How do their margins of error compare?arrow_forwardSuppose that you conduct a study twice, and the second time you use four times as many people as you did the first time. How does the change affect your margin of error? (Assume the other components remain constant.)arrow_forwardOut of a sample of 200 babysitters, 70 percent are girls, and 30 percent are guys. What’s the margin of error for the percentage of female babysitters? Assume 95 percent confidence.What’s the margin of error for the percentage of male babysitters? Assume 95 percent confidence.arrow_forward
- You sample 100 fish in Pond A at the fish hatchery and find that they average 5.5 inches with a standard deviation of 1 inch. Your sample of 100 fish from Pond B has the same mean, but the standard deviation is 2 inches. How do the margins of error compare? (Assume the confidence levels are the same.)arrow_forwardA survey of 1,000 dental patients produces 450 people who floss their teeth adequately. What’s the margin of error for this result? Assume 90 percent confidence.arrow_forwardThe annual aggregate claim amount of an insurer follows a compound Poisson distribution with parameter 1,000. Individual claim amounts follow a Gamma distribution with shape parameter a = 750 and rate parameter λ = 0.25. 1. Generate 20,000 simulated aggregate claim values for the insurer, using a random number generator seed of 955.Display the first five simulated claim values in your answer script using the R function head(). 2. Plot the empirical density function of the simulated aggregate claim values from Question 1, setting the x-axis range from 2,600,000 to 3,300,000 and the y-axis range from 0 to 0.0000045. 3. Suggest a suitable distribution, including its parameters, that approximates the simulated aggregate claim values from Question 1. 4. Generate 20,000 values from your suggested distribution in Question 3 using a random number generator seed of 955. Use the R function head() to display the first five generated values in your answer script. 5. Plot the empirical density…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
An Introduction to Area | Teaching Maths | EasyTeaching; Author: EasyTeaching;https://www.youtube.com/watch?v=_uKKl8R1xBM;License: Standard YouTube License, CC-BY
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=JnLDmw3bbuw;License: Standard YouTube License, CC-BY