Introductory Statistics (10th Edition)
10th Edition
ISBN: 9780321989178
Author: Neil A. Weiss
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 5.2, Problem 29E
In Exercises 5.27–5.30, we have provided the
b. Obtain the standard deviation of the random variable by using one of the formulas given in Definition 5.5.
5.29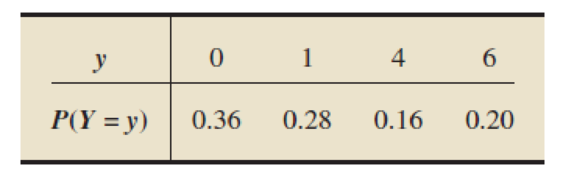 
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
In Exercises 11–18, use the indicated data to construct the frequency distribution. (The data for Exercises 13–16 can be downloaded at TriolaStats.com.)
Burger King Lunch Service Times Refer to Data Set 25 “Fast Food” and use the drive-through service times for Burger King lunches. Begin with a lower class limit of 70 seconds and use a class width of 40 seconds.
In Exercises 13–20, use the data in the table below for sitting adult males and females (based on anthropometric survey data from Gordon, Churchill, et al.). These data are used often in the design of different seats, including aircraft seats, train seats, theater seats, and classroom seats. (Hint: Draw a graph in each case.)
Sitting Back-to-Knee Length (inches)
Find the probability that a female has a back-to-knee length greater than 24.0 in.
EXERCISE 0.3. Roll three dice. Let A = 'the numbers on the first and
second add to 7', B = 'the numbers on the second and third add to 7', and
C = 'the numbers on the third and first add to 7'. Are A, B, C pairwise
independent? Are they mutually independent?
%3D
Chapter 5 Solutions
Introductory Statistics (10th Edition)
Ch. 5.1 - Fill in the blanks. a. A relative-frequency...Ch. 5.1 - Provide an example (other than one discussed in...Ch. 5.1 - Let X denote the number of siblings of a randomly...Ch. 5.1 - Fill in the blank. For a discrete random variable,...Ch. 5.1 - Suppose that you make a large number of...Ch. 5.1 - What rule of probability permits you to obtain any...Ch. 5.1 - A variable x of a finite population has the...Ch. 5.1 - A variable y of a finite population has the...Ch. 5.1 - A variable y of a finite population has the...Ch. 5.1 - A variable x of a finite population has the...
Ch. 5.1 - Space Shuttles. The National Aeronautics and Space...Ch. 5.1 - Persons per Housing Unit. From the document...Ch. 5.1 - Major Hurricanes. The Atlantic Hurricane Database...Ch. 5.1 - Childrens Gender. A certain couple is equally...Ch. 5.1 - Dice. When two balanced dice are rolled, 36...Ch. 5.1 - World Series. The World Series in baseball is won...Ch. 5.1 - Archery. An archer shoots an arrow into a square...Ch. 5.1 - Solar Eclipses. The World Almanac provides...Ch. 5.1 - Black Bear Litters. In the article Reproductive...Ch. 5.1 - All-Numeric Passwords. The technology consultancy...Ch. 5.1 - Suppose that P(Z 1.96) = 0.025. Find P(Z 1.96)....Ch. 5.1 - Suppose that T and Z are random variables. a. If...Ch. 5.1 - Prob. 23ECh. 5.2 - What concept does the mean of a discrete random...Ch. 5.2 - Comparing Investments. Suppose that the random...Ch. 5.2 - In Exercises 5.275.30, we have provided the...Ch. 5.2 - In Exercises 5.275.30, we have provided the...Ch. 5.2 - In Exercises 5.275.30, we have provided the...Ch. 5.2 - In Exercises 5.275.30, we have provided the...Ch. 5.2 - In Exercises 5.315.35, we have provided the...Ch. 5.2 - In Exercises 5.315.35, we have provided the...Ch. 5.2 - In Exercises 5.315.35, we have provided the...Ch. 5.2 - In Exercises 5.315.35, we have provided the...Ch. 5.2 - In Exercises 5.315.35, we have provided the...Ch. 5.2 - World Series. The World Series in baseball is won...Ch. 5.2 - Archery. An archer shoots an arrow into a square...Ch. 5.2 - All-Numeric Passwords. The technology consultancy...Ch. 5.2 - Expected Value. As noted in Definition 5.4 on page...Ch. 5.2 - Evaluating Investments. An investor plans to put...Ch. 5.2 - Homeowners Policy. An insurance company wants to...Ch. 5.2 - Prob. 42ECh. 5.2 - Equipment Breakdowns. A factory manager collected...Ch. 5.2 - Simulation. Let X be the value of a randomly...Ch. 5.2 - Mean as Center of Gravity. Let X be a discrete...Ch. 5.2 - Equipment Breakdowns. Refer to Exercise 5.43....Ch. 5.2 - Equipment Breakdowns. The factory manager in...Ch. 5.3 - In probability and statistics, what is each...Ch. 5.3 - Under what three conditions are repeated trials of...Ch. 5.3 - Explain the significance of binomial coefficients...Ch. 5.3 - Discuss the pros and cons of binomial probability...Ch. 5.3 - What is the binomial distribution?Ch. 5.3 - Suppose that a simple random sample is taken from...Ch. 5.3 - Give two examples of Bernoulli trials other than...Ch. 5.3 - What does the bi in binomial signify?Ch. 5.3 - Compute 3!, 7!, 8!, and 9!.Ch. 5.3 - Find 1!, 2!, 4!, and 6!.Ch. 5.3 - Evaluate the following binomial coefficients. a....Ch. 5.3 - Evaluate the following binomial coefficients. a....Ch. 5.3 - Evaluate the following binomial coefficients. a....Ch. 5.3 - Determine the value of each binomial coefficient....Ch. 5.3 - For each of the following probability histograms...Ch. 5.3 - For each of the following probability histograms...Ch. 5.3 - Pinworm Infestation. Pinworm infestation, which is...Ch. 5.3 - Psychiatric Disorders. The National Institute of...Ch. 5.3 - In each of Exercises 5.675.72, we have provided...Ch. 5.3 - In each of Exercises 5.675.72, we have provided...Ch. 5.3 - In each of Exercises 5.675.72, we have provided...Ch. 5.3 - In each of Exercises 5.675.72, we have provided...Ch. 5.3 - In each of Exercises 5.675.72, we have provided...Ch. 5.3 - In each of Exercises 5.675.72, we have provided...Ch. 5.3 - Prob. 73ECh. 5.3 - Psychiatric Disorders. Use Procedure 5.1 on page...Ch. 5.3 - Tossing a Coin. If we repeatedly toss a balanced...Ch. 5.3 - Rolling a Die. If we repeatedly roll a balanced...Ch. 5.3 - Horse Racing. According to the Daily Racing Form,...Ch. 5.3 - Gestation Periods. The probability is 0.314 that...Ch. 5.3 - Traffic Fatalities and Intoxication. The National...Ch. 5.3 - Multiple-Choice Exams. A student takes a...Ch. 5.3 - Love Stinks? J. Fetto, in the article Love Stinks...Ch. 5.3 - Carbon Tax. A poll commissioned by Friends of the...Ch. 5.3 - Video Games. A pathological video game user (PVGU)...Ch. 5.3 - Recidivism. In the Scientific American article...Ch. 5.3 - Roulette. A success, s, in Bernoulli trials is...Ch. 5.3 - Sampling and the Binomial Distribution. Refer to...Ch. 5.3 - Sampling and the Binomial Distribution. Following...Ch. 5.3 - The Hypergeometric Distribution. In this exercise,...Ch. 5.3 - To illustrate, again consider the Mega Millions...Ch. 5.3 - To illustrate, consider the following problem:...Ch. 5.4 - Identify two uses of Poisson distributions.Ch. 5.4 - Why cant all the probabilities for a Poisson...Ch. 5.4 - For a Poisson random variable, what is the...Ch. 5.4 - What conditions should be satisfied in order to...Ch. 5.4 - Prob. 95ECh. 5.4 - Prob. 96ECh. 5.4 - In each of Exercises 5.965.99, we have provided...Ch. 5.4 - Prob. 98ECh. 5.4 - In each of Exercises 5.965.99, we have provided...Ch. 5.4 - Amusement Ride Safety. Approximately 297 million...Ch. 5.4 - Polonium. In the 1910 article The Probability...Ch. 5.4 - Wasps. M. Goodisman et al. studied patterns in...Ch. 5.4 - Wars. In the paper The Distribution of Wars in...Ch. 5.4 - Motel Reservations. M. Driscoll and N. Weiss...Ch. 5.4 - Cherry Pies. At one time, a well-known restaurant...Ch. 5.4 - Motor-Vehicle Deaths. According to Injury Facts, a...Ch. 5.4 - Prisoners. From the U.S. Census Bureau and the...Ch. 5.4 - The Challenger Disaster. In a letter to the editor...Ch. 5.4 - Fragile X Syndrome. The second-leading genetic...Ch. 5.4 - Holes in One. Refer to the case study on page 223....Ch. 5.4 - A Yellow Lobster! As reported by the Associated...Ch. 5.4 - With regard to the use of a Poisson distribution...Ch. 5.4 - Roughly speaking, you can use the Poisson...Ch. 5 - Fill in the blanks. a. A ______ is a quantitative...Ch. 5 - Prob. 2RPCh. 5 - Prob. 3RPCh. 5 - If you sum the probabilities of the possible...Ch. 5 - A random variable X equals 2 with probability...Ch. 5 - A random variable X has mean 3.6. If you make a...Ch. 5 - Prob. 7RPCh. 5 - Prob. 8RPCh. 5 - Prob. 9RPCh. 5 - List the three requirements for repeated trials of...Ch. 5 - What is the relationship between Bernoulli trials...Ch. 5 - In 10 Bernoulli trials, how many outcomes contain...Ch. 5 - Craps. The game of craps is played by rolling two...Ch. 5 - Following are two probability histograms of...Ch. 5 - Prob. 15RPCh. 5 - Prob. 16RPCh. 5 - ASU Enrollment Summary. According to the Arizona...Ch. 5 - Prob. 18RPCh. 5 - Busy Phone Lines. Refer to the probability...Ch. 5 - Craps. Use the binomial probability formula to...Ch. 5 - Penalty Kicks. In the game of soccer, a penalty...Ch. 5 - Pets. According to JAVMA News, a publication of...Ch. 5 - Pets. Refer to Problem 22. a. Draw a probability...Ch. 5 - Prob. 24RPCh. 5 - Prob. 25RPCh. 5 - Meteoroids. In the article Interstellar Pelting...Ch. 5 - Emphysema. The respiratory disease emphysema,...Ch. 5 - Prob. 28RPCh. 5 - As we reported at the beginning of this chapter,...
Additional Math Textbook Solutions
Find more solutions based on key concepts
TRY IT YOURSELF 2
Determine whether each number describes a population parameter or a sample statistic. Explain...
Elementary Statistics: Picturing the World (7th Edition)
UW Student survey In a University of Wisconsin (UW) study about alcohol abuse among students, 100 of the 40,858...
Statistics: The Art and Science of Learning from Data (4th Edition)
How much time do Americans living in or near cities spend waiting in traffic, and how much does waiting in traf...
Business Statistics: A First Course (7th Edition)
Find how many SDs above the mean price would be predicted to cost.
Intro Stats, Books a la Carte Edition (5th Edition)
In Exercises 9-20, use the data in the following table, which lists drive-thru order accuracy at popular fast f...
Elementary Statistics (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- In Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1 − 1 and n2 − 1.) BMI We know that the mean weight of men is greater than the mean weight of women, and the mean height of men is greater than the mean height of women. A person’s body mass index (BMI) is computed by dividing weight (kg) by the square of height (m). Given below are the BMI statistics for random samples of females and males taken from Data Set 1 “Body Data” in Appendix B. a.Use a 0.05 significance level to test the claim that females and males have the same mean BMI. b.Construct the confidence interval that is appropriate for testing the claim in part (a). c.Do females and males appear to have the same mean BMI?arrow_forwardsolve 1.3.6 please and explain the workarrow_forwardIn Exercises 5–20, assume that the two samples are independent simple random samples selected from normally distributed populations, and do not assume that the population standard deviations are equal. (Note: Answers in Appendix D include technology answers based on Formula 9-1 along with “Table” answers based on Table A-3 with df equal to the smaller of n1 − 1 and n2 − 1.) Color and Cognition Researchers from the University of British Columbia conducted a study to investigate the effects of color on cognitive tasks. Words were displayed on a computer screen with background colors of red and blue. Results from scores on a test of word recall are given below. Higher scores correspond to greater word recall. a. Use a 0.05 significance level to test the claim that the samples are from populations with the same mean. b. Construct a confidence interval appropriate for the hypothesis test in part (a). What is it about the confidence interval that causes us to reach the same conclusion from…arrow_forward
- A random sample of n1 = 10 regions in New England gave the following violent crime rates (per million population). x1: New England Crime Rate 3.2 3.1 4.0 3.2 3.3 4.1 1.8 4.8 2.9 3.1 Another random sample of n2 = 12 regions in the Rocky Mountain states gave the following violent crime rates (per million population). x2: Rocky Mountain Crime Rate 3.7 4.1 4.5 5.1 3.3 4.8 3.5 2.4 3.1 3.5 5.2 2.8 Assume that the crime rate distribution is approximately normal in both regions. Note: If a two-sample t-test is appropriate, for degrees of freedom d.f. not in the Student's t table, use the closest d.f. that is smaller. In some situations, this choice of d.f. may increase the P-value by a small amount and therefore produce a slightly more "conservative" answer.Use a calculator to calculate x1, s1, x2, and s2. (Round your answers to two decimal places.) x1 = s1 = x2 = s2 = (a) Do the data indicate that the violent crime rate in the Rocky Mountain…arrow_forwardpart 1 of 2 If you are a 65% free-throw shooter and the random variable Y denotes the total number of shots in order to make one free-throw, then: Calculate E[Y]. Round to the nearest whole number. part 2 of 2 Calculate Var[Y]. Round to the nearest whole number. 1.4 2.1 3.2 4. 3 1.2 2.1 3.0 4. 3arrow_forwardA random sample of n1 = 10 regions in New England gave the following violent crime rates (per million population). x1: New England Crime Rate 3.3 3.9 4.2 4.1 3.3 4.1 1.8 4.8 2.9 3.1 Another random sample of n2 = 12 regions in the Rocky Mountain states gave the following violent crime rates (per million population). x2: Rocky Mountain Crime Rate 3.7 4.1 4.7 5.5 3.3 4.8 3.5 2.4 3.1 3.5 5.2 2.8 Assume that the crime rate distribution is approximately normal in both regions. Do the data indicate that the violent crime rate in the Rocky Mountain region is higher than in New England? Use ? = 0.01. Solve the problem using both the traditional method and the P-value method. (Test the difference ?1 − ?2. Round the test statistic and critical value to three decimal places.) test statistic critical value Find (or estimate) the P-value. P-value > 0.250 0.125 < P-value < 0.250 0.050 < P-value < 0.125 0.025 < P-value < 0.050 0.005 <…arrow_forward
- A random sample of n1 = 10 regions in New England gave the following violent crime rates (per million population). x1: New England Crime Rate 3.3 3.9 4.2 4.1 3.3 4.1 1.8 4.8 2.9 3.1 Another random sample of n2 = 12 regions in the Rocky Mountain states gave the following violent crime rates (per million population). x2: Rocky Mountain Crime Rate 3.7 4.1 4.7 5.5 3.3 4.8 3.5 2.4 3.1 3.5 5.2 2.8 Assume that the crime rate distribution is approximately normal in both regions. Do the data indicate that the violent crime rate in the Rocky Mountain region is higher than in New England? Use ? = 0.01. Solve the problem using both the traditional method and the P-value method. (Test the difference ?1 − ?2. Round the test statistic and critical value to three decimal places.) test statistic critical value Find (or estimate) the P-value. P-value > 0.2500.125 < P-value < 0.250 0.050 < P-value < 0.1250.025 < P-value < 0.0500.005 <…arrow_forwardA random sample of n1 = 10 regions in New England gave the following violent crime rates (per million population). x1: New England Crime Rate 3.3 3.9 4.2 4.1 3.3 4.1 1.8 4.8 2.9 3.1 Another random sample of n2 = 12 regions in the Rocky Mountain states gave the following violent crime rates (per million population). x2: Rocky Mountain Crime Rate 3.7 4.1 4.7 5.5 3.3 4.8 3.5 2.4 3.1 3.5 5.2 2.8 Assume that the crime rate distribution is approximately normal in both regions. Do the data indicate that the violent crime rate in the Rocky Mountain region is higher than in New England? Use α = 0.01. Solve the problem using both the traditional method and the P-value method. (Test the difference μ1 − μ2. Round the test statistic and critical value to three decimal places.) test statistic critical valuearrow_forwardA random sample of n1 = 10 regions in New England gave the following violent crime rates (per million population). x1: New England Crime Rate 3.5 3.9 4.2 4.1 3.3 4.1 1.8 4.8 2.9 3.1 Another random sample of n2 = 12 regions in the Rocky Mountain states gave the following violent crime rates (per million population). x2: Rocky Mountain Crime Rate 3.7 4.1 4.7 5.5 3.3 4.8 3.5 2.4 3.1 3.5 5.2 2.8 Assume that the crime rate distribution is approximately normal in both regions. (a) Use a calculator to calculate x1, s1, x2, and s2. (Round your answers to four decimal places.) x1=s1=x2=s2= What is the value of the sample test statistic? (Test the difference μ1 − μ2. Round your answer to three decimal places.)arrow_forward
- Score 11-14 15-18 19-22 23-26 27-30 31-34 35-38 Frequency 4 7 8 10 12 7 8 What is the 90th percentile of the students score data? a) 27.64 b) 37.60 c) 31.07 d) 36.70arrow_forwardA random sample of n1 = 10 regions in New England gave the following violent crime rates (per million population). x1: New England Crime Rate 3.5 3.9 4.0 4.1 3.3 4.1 1.8 4.8 2.9 3.1 Another random sample of n2 = 12 regions in the Rocky Mountain states gave the following violent crime rates (per million population). x2: Rocky Mountain Crime Rate 3.7 4.1 4.7 5.1 3.3 4.8 3.5 2.4 3.1 3.5 5.2 2.8 (a) Assume that the crime rate distribution is approximately normal in both regions. Use a calculator to calculate x1, s1, x2, and s2. (Round your answers to two decimal places.) x1 = s1 = x2 = s2 = (b) What is the value of the sample test statistic? Compute the corresponding z or t value as appropriate. (Test the difference μ1 − μ2. Do not use rounded values. Round your answer to three decimal places.) (c) Find a 98% confidence interval for μ1 − μ2. (Round your answers to two decimal places.) lower limit upper limitarrow_forwardA random sample of n1 = 10 regions in New England gave the following violent crime rates (per million population). x1: New England Crime Rate 3.3 3.9 4.2 4.1 3.3 4.1 1.8 4.8 2.9 3.1 Another random sample of n2 = 12 regions in the Rocky Mountain states gave the following violent crime rates (per million population). x2: Rocky Mountain Crime Rate 3.5 4.1 4.5 5.5 3.3 4.8 3.5 2.4 3.1 3.5 5.2 2.8 Assume that the crime rate distribution is approximately normal in both regions. Do the data indicate that the violent crime rate in the Rocky Mountain region is higher than in New England? Use ? = 0.01. Solve the problem using both the traditional method and the P-value method. (Test the difference ?1 − ?2. Round the test statistic and critical value to three decimal places.)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Statistics 4.1 Point Estimators; Author: Dr. Jack L. Jackson II;https://www.youtube.com/watch?v=2MrI0J8XCEE;License: Standard YouTube License, CC-BY
Statistics 101: Point Estimators; Author: Brandon Foltz;https://www.youtube.com/watch?v=4v41z3HwLaM;License: Standard YouTube License, CC-BY
Central limit theorem; Author: 365 Data Science;https://www.youtube.com/watch?v=b5xQmk9veZ4;License: Standard YouTube License, CC-BY
Point Estimate Definition & Example; Author: Prof. Essa;https://www.youtube.com/watch?v=OTVwtvQmSn0;License: Standard Youtube License
Point Estimation; Author: Vamsidhar Ambatipudi;https://www.youtube.com/watch?v=flqhlM2bZWc;License: Standard Youtube License