Chapter 5.1, Problem 6E

(a)

To determine

To draw:The graph for the function $f\left(x\right)=x-2\ln x$.

Answer to Problem 6E

The graph for the function $f\left(x\right)=x-2\ln x$ is drawn.

Explanation of Solution

Given information:

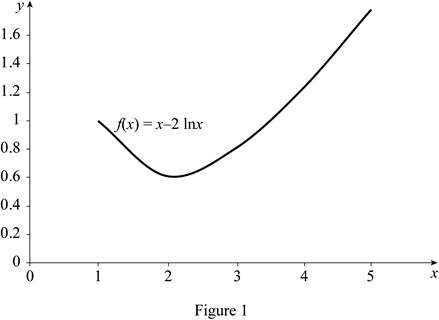
The curve function is $f\left(x\right)=x-2\ln x$.

The region lies in the interval $1\le x\le 5$. So the limits are $a=1$ and $b=5$.

Draw the graph for the function $f\left(x\right)=x-2\ln x$ lies the interval $1\le x\le 5$ as shown in Figure 1.

(b)

(i)

To determine

The area under the graph of f using right endpoints and four rectangles.

Answer to Problem 6E

The area under the graph of f using right endpoints and four rectangles is 4.44.

Explanation of Solution

Draw the graph for the function $f\left(x\right)=x-2\ln x$ with four rectangles using the right endpoints as shown in Figure 2.

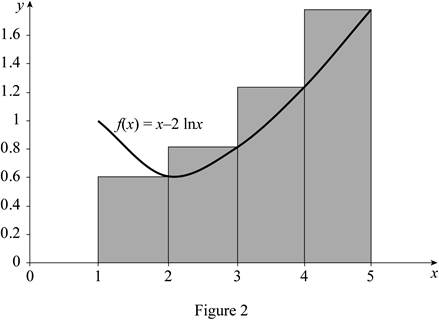
The expression to find the estimate of the areas of n rectangles $\left(R_n\right)$ using right endpoints is shown below:

$R_n=f\left(x_1\right)\Delta x+f\left(x_2\right)\Delta x+\mathrm{...}+f\left(x_n\right)\Delta x$ (1)

Here, the right endpoint height of the first rectangle is $f\left(x_1\right)$, the width is $\Delta x$, the right endpoint height of the second rectangle is $f\left(x_2\right)$, and the right endpoint height of the n^th rectangle is $f\left(x_n\right)$.

Find the width $\left(\Delta x\right)$ using the relation:

$\Delta x=\frac{b-a}{n}$ (2)

Here, the upper limit is b, the lower limit is a, and the number of rectangles is n.

Find the area estimate for four rectangles with right end points:

Substitute 5 for b, 1 for a, and 4 for n in Equation (2).

$\begin{array}{c}\Delta x=\frac{5-1}{4}\\ =1\end{array}$

Refer to Figure 2.

Take the right endpoint height of the first rectangle’s $f\left(x_1\right)$ value as 0.6, the right endpoint height of the second rectangle’s $f\left(x_2\right)$ value as 0.82, the right endpoint height of the third rectangle’s $f\left(x_3\right)$ value as 1.22, and the right endpoint height of the fourth rectangle’s $f\left(x_4\right)$ value as 1.8.

Substitute 4 for n, 0.6 for $f\left(x_1\right)$, 1 for $\Delta x$, 0.82 for $f\left(x_2\right)$, 1.22 for $f\left(x_3\right)$, and 1.8 for $f\left(x_4\right)$ in Equation (1).

$\begin{array}{c}{R}_4=\left(0.6\times 1\right)+\left(0.82\times 1\right)+\left(1.22\times 1\right)+\left(1.8\times 1\right)\\ =0.6+0.82+1.22+1.8\\ =4.44\end{array}$

Therefore, the area under the graph of f using right endpoints for $n=4$ is 4.44.

(ii)

To determine

The area under the graph of f using midpoints and four rectangles.

Answer to Problem 6E

The area under the graph of f using midpoints and four rectangles is 3.93.

Explanation of Solution

Draw the graph for the function $f\left(x\right)=x-2\ln x$ with four rectangles using midpoints as shown in Figure 3.

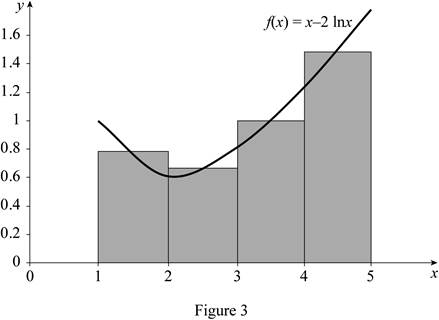
The expression to find the estimate of the areas of n rectangles $\left(M_n\right)$ using midpoints is shown below:

$M_n=f\left(x_1\right)\Delta x+f\left(x_2\right)\Delta x+\mathrm{...}+f\left(x_n\right)\Delta x$ (3)

Here, the midpoint height of the first rectangle is $f\left(x_1\right)$, the width is $\Delta x$, the midpoint height of the second rectangle is $f\left(x_2\right)$, and the midpoint height of n^th rectangle is $f\left(x_n\right)$.

Find the area estimate for four rectangles with mid points:

Refer to Figure 3.

Take the midpoint height of the first rectangle’s $f\left(x_1\right)$ value as 0.78, the midpoint height of the second rectangle’s $f\left(x_2\right)$ value as 0.67, the midpoint height of the third rectangle’s $f\left(x_3\right)$ value as 1, and the midpoint height of the fourth rectangle’s $f\left(x_4\right)$ value as 1.48.

Substitute 4 for n, 0.78 for $f\left(x_1\right)$, 1 for $\Delta x$, 0.67 for $f\left(x_2\right)$, 1 for $f\left(x_3\right)$, and 1.48 for $f\left(x_4\right)$ in Equation (3).

$\begin{array}{c}{M}_4=\left(0.78\times 1\right)+\left(0.67\times 1\right)+\left(1\times 1\right)+\left(1.48\times 1\right)\\ =0.78+0.67+1+1.48\\ =3.93\end{array}$

Therefore, the area under the graph of f using mid points for $n=4$ is 3.93.

(c)

(i)

To determine

The area under the graph of f using right endpoints and eight rectangles.

Answer to Problem 6E

The area under the graph of f using right endpoints and eight rectangles is 3.94.

Explanation of Solution

Draw the graph for the function $f\left(x\right)=x-2\ln x$ with eight rectangles using the right endpoints as shown in Figure 4.

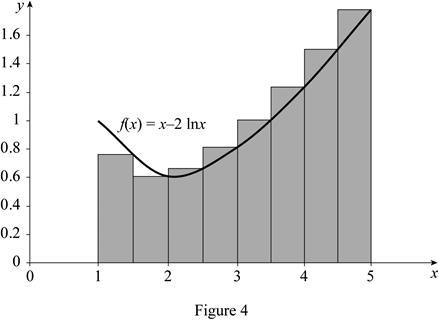
Find the area estimate for eight rectangles with right end points:

Substitute 5 for b, 1 for a, and 8 for n in Equation (2).

$\begin{array}{c}\Delta x=\frac{5-1}{8}\\ =0.5\end{array}$

Refer to Figure 4.

Take the right endpoint height of the first rectangle’s $f\left(x_1\right)$ value as 0.76, the right endpoint height of the second rectangle’s $f\left(x_2\right)$ value as 0.6, the right endpoint height of the third rectangle’s $f\left(x_3\right)$ value as 0.68, the right endpoint height of the fourth rectangle’s $f\left(x_4\right)$ value as 0.82, the right endpoint height of the fifth rectangle’s $f\left(x_5\right)$ value as 1, the right endpoint height of the sixth rectangle’s $f\left(x_6\right)$ value as 1.22, the right endpoint height of the seventh rectangle’s $f\left(x_7\right)$ value as 1.5, and the right endpoint height of the eighth rectangle’s $f\left(x_8\right)$ value as 1.8.

Substitute 8 for n, 0.76 for $f\left(x_1\right)$, 0.5 for $\Delta x$, 0.6 for $f\left(x_2\right)$, 0.68 for $f\left(x_3\right)$, 0.82 for $f\left(x_4\right)$, 1 for $f\left(x_5\right)$, 1.22 for $f\left(x_6\right)$, 1.5 for $f\left(x_7\right)$, and 1.8 for $f\left(x_8\right)$ in Equation (1).

$\begin{array}{c}{R}_8=\left[\begin{array}{l}\left(0.76\times 0.5\right)+\left(0.6\times 0.5\right)+\left(0.68\times 0.5\right)+\left(0.82\times 0.5\right)\\ +\left(1\times 0.5\right)+\left(1.22\times 0.5\right)+\left(1.5\times 0.5\right)+\left(1.8\times 0.5\right)\end{array}\right]\\ =0.38+0.3+0.34+0.41+0.25+0.61+0.75+0.9\\ =3.94\end{array}$

Therefore, the area under the graph of f using right endpoints for $n=8$ is 3.94.

(ii)

To determine

The area under the graph of f using midpoints and eight rectangles.

Answer to Problem 6E

The area under the graph of f using midpoints and eight rectangles is 3.975.

Explanation of Solution

Draw the graph for the function $f\left(x\right)=x-2\ln x$ with eight rectangles using midpoints as shown in Figure 5.

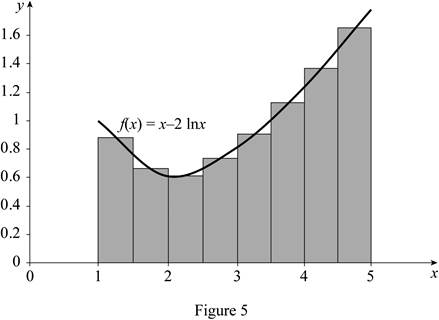
Find the area estimate for eight rectangles with mid points:

Refer to Figure 5.

Take the midpoint height of the first rectangle’s $f\left(x_1\right)$ value as 0.87, the midpoint height of the second rectangle’s $f\left(x_2\right)$ value as 0.68, the midpoint height of the third rectangle’s $f\left(x_3\right)$ value as 0.6, the midpoint height of the fourth rectangle’s $f\left(x_4\right)$ value as 0.74, the midpoint height of the fifth rectangle’s $f\left(x_5\right)$ value as 0.9, the midpoint height of the sixth rectangle’s $f\left(x_6\right)$ value as 1.12, the midpoint height of the seventh rectangle’s $f\left(x_7\right)$ value as 1.38, and the midpoint height of the eighth rectangle’s $f\left(x_8\right)$ value as 1.66.

Substitute 8 for n, 0.87 for $f\left(x_1\right)$, 0.5 for $\Delta x$, 0.68 for $f\left(x_2\right)$, 0.6 for $f\left(x_3\right)$, 0.74 for $f\left(x_4\right)$, 0.9 for $f\left(x_5\right)$, 1.12 for $f\left(x_6\right)$, 1.38 for $f\left(x_7\right)$, and 1.66 for $f\left(x_8\right)$ in Equation (3).

$\begin{array}{c}{M}_8=\left[\begin{array}{l}\left(0.87\times 0.5\right)+\left(0.68\times 0.5\right)+\left(0.6\times 0.5\right)+\left(0.74\times 0.5\right)\\ +\left(0.9\times 0.5\right)+\left(1.12\times 0.5\right)+\left(1.38\times 0.5\right)+\left(1.66\times 0.5\right)\end{array}\right]\\ =0.435+0.34+0.3+0.37+0.45+0.56+0.69+0.83\\ =3.975\end{array}$

Therefore, the area under the graph of f using mid points for $n=8$ is 3.975.