
Concept explainers
A solid steel bar has a square cross section of side b and is supported as shown. Knowing that for steel ρ = 7860 kg/m3, determine the dimension b for which the maximum normal stress due to bending is (a) 10 MPa, (b) 50 MPa.
Fig. P5.33
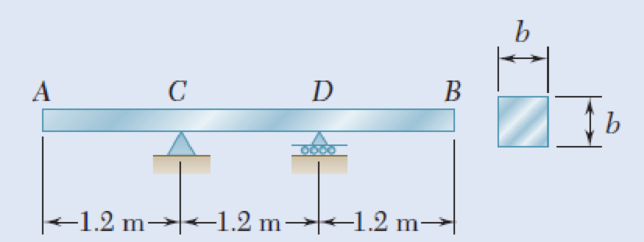
(a)
the dimension b.
Answer to Problem 33P
The dimension b of the square cross section is
Explanation of Solution
Given information:
The maximum normal stress due to bending is 10 MPa.
Determine the weight density
Here, the mass density of the bar is
Consider the acceleration due to gravity as
Substitute
Determine the dead load (W) of the solid steel bar using the relation.
Here, the cross sectional area of the steel bar is A, the length of the beam is L, and the dimension of the bar is d.
Convert the mass density into weight density as follows;
Substitute
Determine the reactions of the beam.
Show the free-body diagram of the beam as in Figure 1.
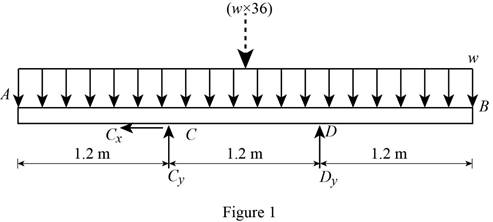
Determine the vertical reaction at point C by taking moment at point D.
Show the free-body diagram of the sections as in Figure 2.
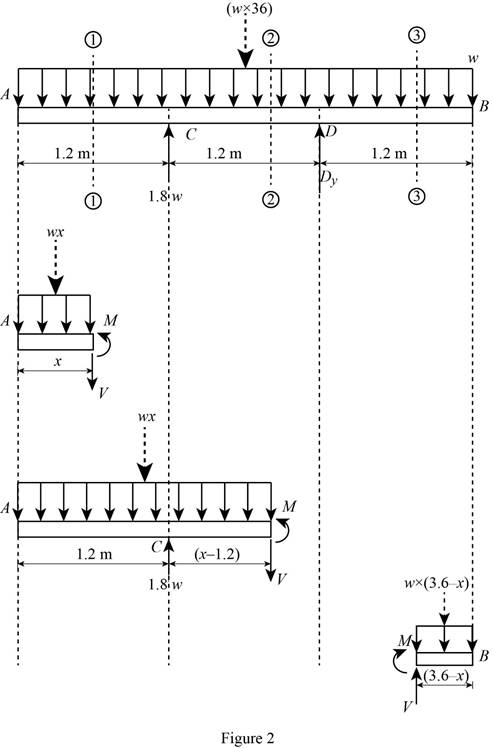
Region AC (Section 1-1):
Determine the bending moment at the section by taking moment about the section.
Region CD (Section 2-2):
Determine the bending moment at the section by taking moment about the section.
Region DB (Section 3-3):
Determine the bending moment at the section by taking moment about the section.
Bending moment values:
Show the calculated bending moment values as in Table 1.
| Location (x) m | Bending moment (M) N-m |
| A (0 m) | 0 |
| C (1-1) (1.2 m) | –0.72w |
| C (2-2) (1.2 m) | –0.72w |
| Mid-point (1.8 m) | –0.54w |
| D (2-2) (2.4 m) | –0.72w |
| D (3-3) (2.4 m) | –0.72w |
| B (3.6 m) | 0 |
Plot the bending moment diagram as in Figure 3.
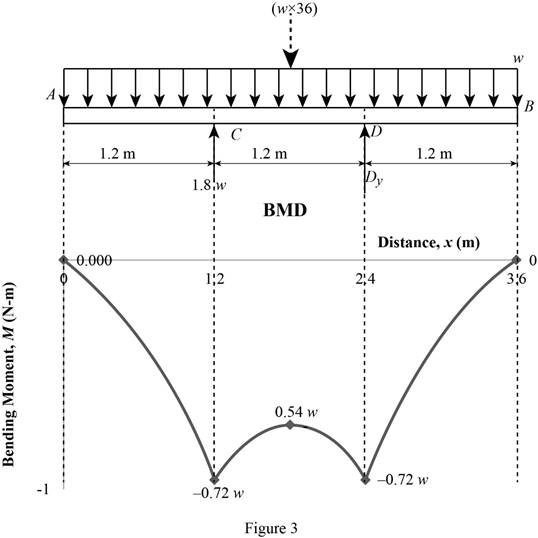
Refer to Figure 3;
The maximum bending moment is
Determine the section modulus (S) of the square section using the equation.
Determine the maximum normal stress
Substitute
Substitute 10 MPa for
Therefore, the dimension b of the square cross section is
(b)
the dimension b.
Answer to Problem 33P
The dimension b of the square cross section is
Explanation of Solution
Given information:
The maximum normal stress due to bending is 50 MPa.
Determine the weight density
Here, the mass density of the bar is
Consider the acceleration due to gravity as
Substitute
Determine the dead load (W) of the solid steel bar using the relation.
Here, the cross sectional area of the steel bar is A, the length of the beam is L, and the dimension of the bar is d.
Convert the mass density into weight density as follows;
Substitute
Determine the reactions of the beam.
Show the free-body diagram of the beam as in Figure 4.
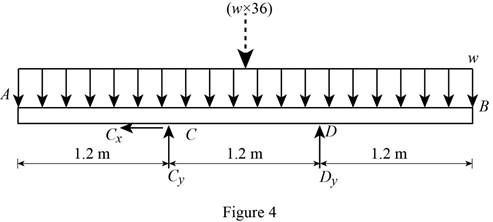
Determine the vertical reaction at point C by taking moment at point D.
Show the free-body diagram of the sections as in Figure 5.
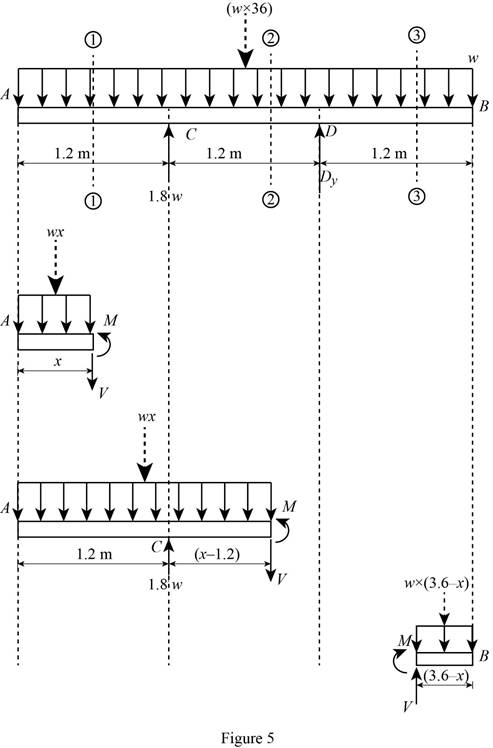
Region AC (Section 1-1):
Determine the bending moment at the section by taking moment about the section.
Region CD (Section 2-2):
Determine the bending moment at the section by taking moment about the section.
Region DB (Section 3-3):
Determine the bending moment at the section by taking moment about the section.
Bending moment values:
Show the calculated bending moment values as in Table 2.
| Location (x) m | Bending moment (M) N-m |
| A (0 m) | 0 |
| C (1-1) (1.2 m) | –0.72w |
| C (2-2) (1.2 m) | –0.72w |
| Mid-point (1.8 m) | –0.54w |
| D (2-2) (2.4 m) | –0.72w |
| D (3-3) (2.4 m) | –0.72w |
| B (3.6 m) | 0 |
Plot the bending moment diagram as in Figure 6.
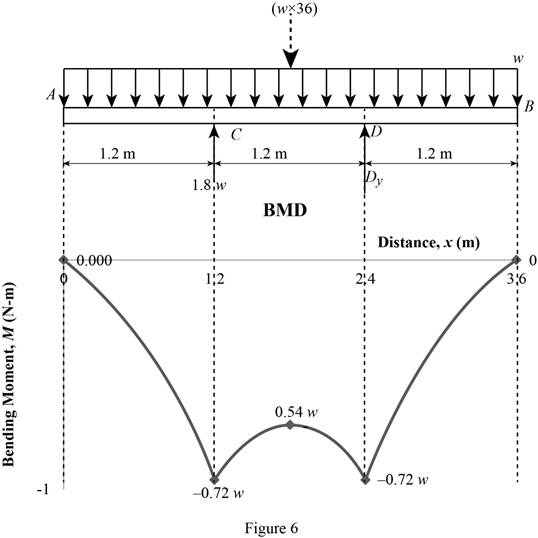
Refer to the Figure 6;
The maximum bending moment is
Determine the section modulus (S) of the square section using the equation.
Determine the maximum normal stress
Substitute
Substitute 50 MPa for
Therefore, the dimension b of the square cross section is
Want to see more full solutions like this?
Chapter 5 Solutions
EBK MECHANICS OF MATERIALS
- No. 3arrow_forward4.37 A W 200 x 31.3 rolled-steel beam is subjected to a couple M of moment 45 kN-m. Knowing that E= Z00GPA, v=0.29, determine (a) the radius of curvature P. (b) the radius of curvature p' of a transverse cross section. SOLUTIONarrow_forwardThe couple M is applied to a beam of the cross section shown in a plane forming an angle β with the vertical. Determine the stress at (a) point A, (b) point B, (c) point D.arrow_forward
- A timber beam AB of length L and rectangular cross section carries a single concentrated load P at its midpoint C. (a) Show that the ratio Tm/ m of the maximum values of the shearing and normal stresses in the beam is equal to h/2L, where h and L are, respectively, the depth and the length of the beam. (b) Determine the depth h and the width b of the beam, knowing that L = 2 m, P = 40 kN, 7m = 960 kPa, and om = 12 MPa.arrow_forward2.13 A steel plate, which is 1.5 m by 1.5 m and 30 mm thick, is lifted by four cables attached to its corners that meet at a point that is 2 m above the plate. Determine the required cross-sectional area of the cables if the stress in them is not to exceed 20 MPa. Steel plate Prob. 2.13 Cablesarrow_forwardA copper strip (E = 105 GPa) and an aluminum strip (E = 75 GPa) are bonded together to form the composite beam shown. Knowing that the beam is bent about a horizontal axis by a couple of moment M = 35 N.m, determine the maximum stress in (a) the aluminum strip, (b) the copper strip. Fig. P4.39 Aluminum Copper 24 mm 6 mm 6 mmarrow_forward
- A solid steel rod of diameter d is supported as shown. Knowing that for steel γ= 490 lb/ft3, determine the smallest diameter d that can be used if the normal stress due to bending is not to exceed 4 ksiarrow_forward250 mm PROBLEM 4.3 18 mm The wide-flange beam shown is made of a high-strength, low alloy steel for which o, = 450 MPa. Using a factor of safety of 3.0, determine the largest couple that can be applied to the beam when it is bent about C 360 mm M. + 10 mm the z axis. [Ans. 243.3 kNm] 18 mm Fig. P4.3 and P4.4 PROBLEM 4.4 Solve Prob, 4.3. assuming thatarrow_forwardTwo wooden boards, measuring 15 mm thick and 225 mm wide, are joined by the socket joint shown. Knowing that the wood employed will break when the average shear stress reaches 10 MPa, determine the intensity P of the axial force that will break the joint.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





