
Concept explainers
A real estate agent is considering changing her cell phone plan. There are three plans to choose from, all of which involve a monthly service charge of $20. Plan A has a cost of $.45 a minute for daytime calls and $.20 a minute for evening calls. Plan B has a charge of $.55 a minute for daytime calls and $.15 a minute for evening calls. Plan C has a flat rate of $80 with 200 minutes of calls allowed per month and a charge of $.40 per minute beyond that, day or evening.
a. Determine that total charge under each plan for this case: 120 minutes of day calls and 40 minutes of evening calls in a month.
b. Prepare a graph that shows total monthly cost for each plan versus daytime call minutes.
c. If the agent will use the service for daytime calls, over what range of call minutes will each plan be optimal?
d. Suppose that the agent expects both daytime and evening calls. At what point (i.e., percentage of call minutes for daytime calls) would she be indifferent between plans A and B?
a)
To determine: The total charge of each plan for 120 minutes of day calls and 40 minutes of evening calls.
Introduction: Capacity planning is the process of planning the required production output based on the requirement or the demand that is predicted.
Answer to Problem 6P
Explanation of Solution
Given information:
A real estate is considered changing her cell phone plan which incurs a monthly service charge of $20. There are three plans available.
Plan A: $0.45 per minute for a day calls and $0.20 per minute for evening calls.
Plan B: $0.55 per minute for a day calls and $0.15 per minute for evening calls.
Plan C: $80 for allowed 200 calls per month and $0.40 per minutes beyond that irrespective of day or evening
Calculate the total cost for Plan A:
It is calculated by adding the monthly service charge, the multiple of cost per minute of day calls and total minutes given for day calls, and the multiple of cost per minute of evening calls and total minutes given for evening calls.
Hence, the total cost for Plan A is $82.
Calculate the total cost for Plan B:
It is calculated by adding the monthly service charge, the multiple of cost per minute of day calls and total minutes given for day calls, and the multiple of cost per minute of evening calls and total minutes given for evening calls.
Hence, the total cost for Plan B is $92.
Calculate the total cost for Plan C:
It is calculated by adding monthly service charge, call cost for the allowed 200 minutes, and the multiple of call minutes beyond 200 and the cost per minutes. The total call minutes is 160 (120+40). As it does not exceed 200 minutes, there would 0 remaining minutes.
Hence, the total cost for Plan C is $100.
b)
To prepare: A graph for monthly charge for each plan versus day time minutes.
Introduction: Capacity planning is the process of planning the required production output based on the requirement or the demand that is predicted.
Answer to Problem 6P
Explanation of Solution
Given information:
A real estate is considered changing her cellphone plan which incurs a monthly service charge of $20. There are three plans available.
Plan A: $0.45 per minute for a day calls and $0.20 per minute for evening calls.
Plan B: $0.55 per minute for a day calls and $0.15 per minute for evening calls.
Plan C: $80 for allowed 200 calls per month and $0.40 per minutes beyond that irrespective of day or evening
Prepare a graph of monthly charge for each plan versus day time minutes:
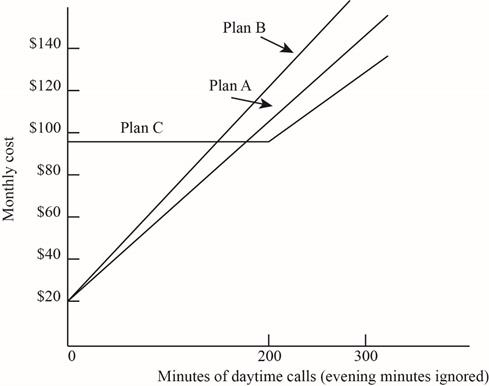
c)
To determine: The optimal call minutes for each plan if the agent would use only day calls.
Introduction: Capacity planning is the process of planning the required production output based on the requirement or the demand that is predicted.
Answer to Problem 6P
Explanation of Solution
Given information:
A real estate is considered changing her cellphone plan which incurs a monthly service charge of $20. There are three plans available.
Plan A: $0.45 per minute for a day calls and $0.20 per minute for evening calls.
Plan B: $0.55 per minute for a day calls and $0.15 per minute for evening calls.
Plan C: $80 for allowed 200 calls per month and $0.40 per minutes beyond that irrespective of day or evening
Determine the optimal call minutes for each plan if the agent would use only day calls:
D refers to day time calls
The volume of Plan B is more than Plan A. Hence, it should be omitted, as it would obvious have high cost.
Calculate the total cost for Plan C:
It is calculated by adding monthly service charge, call cost for the allowed 200 minutes, and the multiple of call minutes beyond 200 and the cost per minutes. The total call minutes is 160 (120+40). As it does not exceed 200 minutes, there would 0 remaining minutes.
Hence, the total cost for Plan C is $100.
Determined the value of D in the equation of Plan A by comparing the equation with the total cost of Plan C:
The equation of Plan A (considering the day calls) should be compared with the total cost of Plan C.
Hence, the day call minutes are 177.78 minutes.
Conclusion: Plan A would be optimal when the day call minutes are less than 177.78 minutes and Plan C would be optional when it exceeds up to 200 minutes.
d)
To determine: The percentage of call minutes would be indifferent between Plan A and Plan B if the agent would both day calls and evening calls.
Introduction: Capacity planning is the process of planning the required production output based on the requirement or the demand that is predicted.
Answer to Problem 6P
Explanation of Solution
Given information:
A real estate is considered changing her cellphone plan which incurs a monthly service charge of $20. There are three plans available.
Plan A: $0.45 per minute for a day calls and $0.20 per minute for evening calls.
Plan B: $0.55 per minute for a day calls and $0.15 per minute for evening calls.
Plan C: $80 for allowed 200 calls per month and $0.40 per minutes beyond that irrespective of day or evening
Determine the percentage of call minutes would be indifferent between Plan A and Plan B if the agent would both day calls and evening calls:
D refers to day time calls
E refers to evening calls
Compare the equations to solve D:
The equation of Plan A and Plan B considering both day and evening calls should be compared to determine the value of D.
It should that day calls are half of the evening calls.
For example: If E=100 minutes,
It states the following equations:
Hence, at 33.33% of total call time, the agent would be indifferent between the plans A and B.
Want to see more full solutions like this?
Chapter 5 Solutions
EBK OPERATIONS MANAGEMENT
- A real estate agent is considering changing her cellphone plan. There are three plans to choose from, all of which involve a weekly service charge of 45.00 dollars. Plan A has a cost of 55 cents a minute for daytime calls and 25 cents a minute for evening calls. Plan B has a charge of 65 cents a minute for daytime calls and 15 cents a minute for evening calls. Plan C has a flat rate of 75.00 dollars with 200 minutes of calls allowed per week and a charge of 45 cents per minute beyond that, day or evening.1. The best Plan is _____2. The total charge is _____ dollarsDetermine the best plan and its total charge at 130 minutes of day calls and 50 minutes of evening calls in a weekarrow_forwardA real estate agent is considering changing her land line phone plan. There are three plans to choose from, all of which involve a monthly service charge of $20. Plan A has a cost of $.43 a minute for daytime calls and $.18 a minute for evening calls. Plan B has a charge of $.53 a minute for daytime calls and $.15 a minute for evening calls. Plan C has a flat rate of $80 with 250 minutes of calls allowed per month and a charge of $.40 per minute beyond that, day or evening. a. Determine the total charge under each plan for this case: 140 minutes of day calls and 60 minutes of evening calls in a month. (Do not round intermediate calculations. Round your answer to 2 decimal places.) b. If the agent will only use the service for daytime calls, over what range of call minutes will each plan be optimal? (Round each answer to the nearest whole number. Include the indifference point itself in each answer.) c. Suppose that the agent expects both daytime and evening calls. At what point…arrow_forwardAsaparrow_forward
- Winchester Hospital is a privately owned institution. The hospital is at full capacity, but the governing board would like to see an increase in revenue. They’ve tasked you, the hospital administrator, with finding ways to accomplish this. If you are able to raise revenue, the board will provide you with a significant year-end bonus. Currently, 50% of Winchester’s rooms can be converted from having one bed to having two beds, allowing for more patients to be admitted. Doctors, nurses, and other hospital staff are firmly against this move, especially because additional hiring is not planned. These stakeholders make up the vast majority of the hospital workforce. Evaluate this situation using both the utilitarianism and individualistic (ethical egoism) approaches. Define each approach and describe how each would resolve the decision. What would you expect the outcome of each decision to be? Support your conclusions with facts from the situation.arrow_forwardA real estate agent is considering changing her cell phone plan. There are three plans to choosefrom, all of which involve a monthly service charge of $20. Plan A has a cost of $.45 a minute fordaytime calls and $.20 a minute for evening calls. Plan B has a charge of $.55 a minute for daytime calls and $.15 a minute for evening calls. Plan C has a flat rate of $80 with 200 minutes ofcalls allowed per month and a charge of $.40 per minute beyond that, day or evening.a. Determine the total charge under each plan for this case: 120 minutes of day calls and 40 minutes of evening calls in a month.arrow_forwardAs part of their application for a loan to buy Lakeside Farm, a property they hope to develop as a bed-and-breakfast operation, the prospective owners have projected: Monthly fixed cost (loan payment, taxes, insurance, maintenance) $6000 Variable cost per occupied room per night $ 20 Revenue per occupied room per night $ 75 Write the expression for total cost per month. Assume 30 days per month. Write the expression for total revenue per month. How many rooms they need to sell per night in order to break even? Suppose 5 rooms can be sold per night, how much they should charge per night in order to breakeven?arrow_forward
- A 3 year-old a computer-controlled fabric cutting machine, which had a $25,000 purchasing price, has a current market (trade-in) value of $10,000 and expected O&M costs of $4,000, increasing by 1,000 per year. The machine is required to have an immediate repair that costs $2,000. The estimated market values are expected to decline by 20% annually (going forward). The machine can be used for another 7 years at most. The new machine has a $40,000 purchasing price. The new machine's O&M cost is estimated to be $4,000 for the first year, decreasing at an annual rate of $100 thereafter. The firm's MARR is 10%. Assume a unique minimum AEC(10%) for both machines (both the current and replacement machine). Using the information above, determine the economic service life along with the optimum annual equivalent cost of the defender (This is an infinite Horizon decision problem). a) n=4 and AEC=Between $8,400 and $8,800 b) n=4 and AEC=Between $8,000 and $8,400 c) n=5 and AEC=Between $8,400 and…arrow_forwardEstimate the cost of a 0.75 million gallon per day (MGD) induced-draft packed tower for air-stripping trihalomethanes from drinking water if the cost for a 2.9-MGD tower is $153,200. The exponent in the cost-capacity equation is 0.47. The cost of a 0.75 million gallon per day induced-draft packed tower is $arrow_forwardPrescribed fire is an important tool for foresters. A recent article describes how decision analysis is used to decide when, where and what to burn. In one example, a number of areas in the Tahoe National Forest in California had been logged and were being prepared for replanting. Preparation included prescribed burning, and two possible treatments were available: burning the slash as it lay on the ground, or “yarding of and merchantable material” (YUM) prior to burning. The latter treatment involves using heavy equipment to pile the slash. YUM reduces the difficulty of controlling the burn but costs an additional $100 per acre. In deciding between the two treatments two uncertainties were considered critical. The first was how the fire would behave under each scenario. For example, the buyer could be fully successful, problems could arise which could be controlled eventually, or the fire could escape entailing considerable losses. Second if problems developed, they could result in…arrow_forward
- You have two design options for your new line of high-resolution monitors for Computer-Aided Design (CAD)workstations. The production run is for 110,000 units. Design option A has a .90 probability of yielding 65good monitors per 100 and a .10 probability of yielding 70good monitors per 100. This design will cost $1,000,000. Design option B has a .80 probability of yielding 65good units per 100 and a .20 probability of yielding 60good units per 100. This design will cost $1,350,000. Good or bad, each monitor will cost $75. Each good monitor will sell for $150. Bad monitors are destroyed and have no salvage value. We ignore any disposal costs in this problem. Demonstrate how decision trees can be used in order to choose the design option based on the above situation. Calculate the expected monetary value (EMV) of each option and determine which option you will propose.arrow_forwardSpartan Castings must implement a manufacturing process that reduces the amount of particulates emitted into the atmosphere. Two processes have been identified that provide the same level of particulate reduction. The first process is expected to incur $350,000 of fixed cost and add $50 of variable cost to each casting Spartan produces. The second process has fixed costs of $150,000 and adds $90 of variable cost per casting.a. What is the break-even quantity beyond which the first process is more attractive?b. What is the difference in total cost if the quantity produced is 10,000?arrow_forwardMars Incorporated is interested in going to market with a new fuel savings device that attaches to electrically powered industrial vehicles. The device, code named "Python," promises to save up to 15% of the electrical power required to operate the average electric forklift. Mars expects that modest demand expected during the introductory year will be followed by a steady increase in demand in subsequent years. The extent of this increase in demand will be based on customer's expectations regarding the future cost of electricity, which is shown in Table 1. Mars expects to sell the device for $300 each, and does not expect to be able to raise its price over the foreseeable future. Mars is faced with two alternatives: ≻Alternative 1: Make the device themselves, which requires an initial outlay of $450,000 in plant and equipment and a variable cost of $175 per unit. ≻Alternative 2: Outsource the production, which requires no initial investment, but incurs a per unit cost…arrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
