Chapter 5, Problem 3SP

A car with a mass of 1100 kg is traveling around a curve with a radius of 50 m at a constant speed of 25 m/s (56 MPH). The curve is banked at an angle of 12 degrees.

1. a. What is the magnitude of the centripetal acceleration of the car?
2. b. What is the magnitude of the centripetal force required to produce this acceleration?
3. c. What is the magnitude of the vertical component of the normal force acting upon the car to counter the weight of the car?
4. d. Draw a diagram of the car (as in fig. 5.8) on the banked curve. Draw to scale the vertical component of the normal force. Using this diagram, find the magnitude of the total normal force, which is perpendicular to the surface of the road.
5. e. Using your diagram, estimate the magnitude of the horizontal component of the normal force. Is this component sufficient to provide the centripetal force?

To determine

The magnitude of the centripetal acceleration of the car.

Answer to Problem 3SP

The magnitude of the centripetal acceleration of the car is $12.5{\text{ m/s}}^2$.

Explanation of Solution

Given Info: The radius of the curve is and the speed of the car is $25\text{ m/s}$.

Write the equation for the centripetal acceleration.

$a_c=\frac{v^2}{r}$

Here,

$a_c$ is the centripetal acceleration of the car

$v$ is the speed of the car

$r$ is the radius of the curve

Substitute $25\text{ m/s}$ for $v$ and $50\text{ m}$ for $r$ in the above equation to find $a_c$.

$\begin{array}{c}{a}_c=\frac{{\left(\text{25 m/s}\right)}^2}{\text{50 m}}\\ =12.5{\text{ m/s}}^2\end{array}$

Conclusion:

Thus the magnitude of the centripetal acceleration of the car is $12.5{\text{ m/s}}^2$.

To determine

The magnitude of the centripetal force required to produce the centripetal acceleration.

Answer to Problem 3SP

The magnitude of the centripetal force required to produce the centripetal acceleration is $13.75\text{ kN}$.

Explanation of Solution

Given Info: The mass of the car is $1100\text{ kg}$.

Write the equation for centripetal force.

$F_c=m{a}_c$

Here,

$F_c$ is the magnitude of the centripetal force

$m$ is the mass of the car

Substitute $1100\text{ kg}$ for $m$ and $12.5{\text{ m/s}}^2$ for $a_c$ in the above equation to find $F_c$.

$\begin{array}{c}{F}_c=\left(1100\text{ kg}\right)\left(12.5{\text{ m/s}}^2\right)\\ =13750\text{ N}\\ =13.75\text{ kN}\end{array}$

Conclusion:

Thus the magnitude of the centripetal force required to produce the centripetal acceleration is $13.75\text{ kN}$.

To determine

The magnitude of the vertical component of the normal force acting upon the car to counter the weight of the car.

Answer to Problem 3SP

The magnitude of the vertical component of the normal force acting upon the car to counter the weight of the car is $10.8\text{ kN}$.

Explanation of Solution

Given Info: The mass of the car is $1100\text{ kg}$.

The vertical component of the normal force acts to counter the weight of the car so that vertical component of normal force is equal to the weight of the car.

Write the equation for the weight of the car.

$W=mg$

Here,

$W$ is the weight of the car

$g$ is the acceleration due to gravity

The value of $g$ is $9.8{\text{ m/s}}^2$.

Substitute $1100\text{ kg}$ for $m$ and $9.8{\text{ m/s}}^2$ for $g$ in the above equation to find $W$.

$\begin{array}{c}W=\left(1100\text{ kg}\right)\left(9.8{\text{ m/s}}^2\right)\\ =10.8\times {10}^3\text{ N}\\ =10.8\text{ kN}\end{array}$

Conclusion:

Thus the magnitude of the vertical component of the normal force acting upon the car to counter the weight of the car is $10.8\text{ kN}$.

To determine

Diagram of the car on the banked curve to scale the vertical component of the normal force and determine the magnitude of the total normal force.

Answer to Problem 3SP

The diagram of the car on the banked curve is

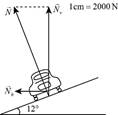
and the magnitude of the total normal force is $11\text{ kN}$.

Explanation of Solution

Given Info: The angle of banking of the curve is $12°$.

The diagram of the car in the curve is shown in figure 1.

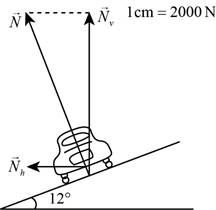
Figure 1

Write the equation for the vertical component of the normal force.

$N_v=\left|N\right|\cos \theta$

Here,

$N_v$ is the vertical component of the normal force

$\left|N\right|$ is the magnitude of the total normal force

$\theta$ is the angle of banking

Rewrite the above equation for $\left|N\right|$.

$\left|N\right|=\frac{N_v}{\cos \theta }$

Substitute $10.8\text{ kN}$ for $N_v$ and $12°$ for $\theta$ in the above equation to find $\left|N\right|$.

$\begin{array}{c}\left|N\right|=\frac{10.8\text{ kN}}{\cos 12°}\\ =11\text{ kN}\end{array}$

Conclusion:

Thus the diagram of the car on the curve is drawn in figure 1 and the magnitude of the total normal force is $11\text{ kN}$.

To determine

The magnitude of the horizontal component of the normal force and whether it is sufficient to provide the centripetal force.

Answer to Problem 3SP

The magnitude of the horizontal component of the normal force is $2.29\text{ kN}$ and it is not sufficient to provide the centripetal force.

Explanation of Solution

Given Info: The angle of banking of the curve is $12°$.

Write the equation for the horizontal component of the normal force.

$N_h=\left|N\right|\sin \theta$

Here,

$N_h$ is the horizontal component of the normal force

Substitute $11\text{ kN}$ for $\left|N\right|$ and $12°$ for $\theta$ in the above equation to find $N_h$.

$\begin{array}{c}{N}_h=\left(11\text{ kN}\right)\sin 12°\\ =2.29\text{ kN}\end{array}$

$N_h<<F_c$

Conclusion:

Thus the magnitude of the horizontal component of the normal force is $2.29\text{ kN}$ and it is not sufficient to provide the centripetal force.