
Concept explainers
The airplane is blown off course by wind in the directions shown. Use the parallelogram rule and rank from highest to lowest the resulting speed across the ground.
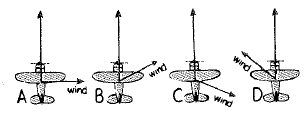
To rank: The airplanes resulting speed from highest to lowest.
Answer to Problem 17A
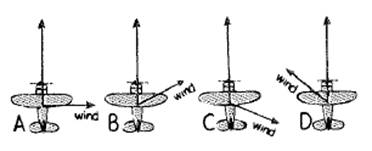
D >B> A> C
Explanation of Solution
Given:
Airplanes along with wind direction are shown below.
Formula used:
According to parallelogram law, if two vectors are represented along the two sides of the parallelogram then their vector sum represents the resultant of two vectors in terms of magnitude and direction.
Calculation:
Consider the figure shown below.
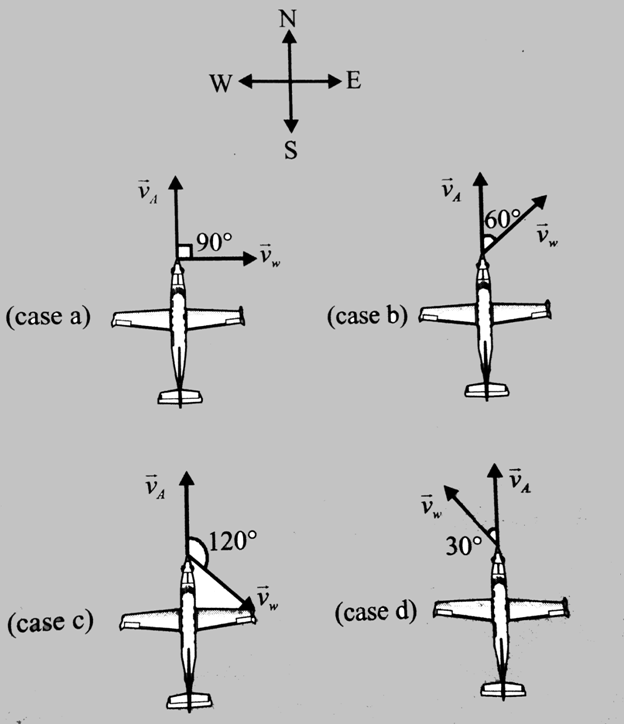
 is the vector component of wind velocity and
is the vector component of wind velocity and 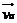 is the vector component of airplane velocity. If by directions provided in the question, angles are calculated. Then, it is quite obvious the airplane in which the wind direction is in the direction of airplane or nearby will move faster across the ground and the one in which the wind velocity is exactly opposite or in nearby directions will move slower.
is the vector component of airplane velocity. If by directions provided in the question, angles are calculated. Then, it is quite obvious the airplane in which the wind direction is in the direction of airplane or nearby will move faster across the ground and the one in which the wind velocity is exactly opposite or in nearby directions will move slower.
In the above diagram, wind velocity and airplane velocity is represented with directions. The airplane is moving in the North direction and accordingly wind direction is varying in each case. According to parallelogram law, the resultant of two vectors is the sum of their vectors concerning their directions and magnitude.
So, D will move fastest as it has minimum angle compared to airplane direction. Then, C then A. But, B will be the last one because the wind direction is moving towards South-East, which is quite opposite to the direction in which the airplane is moving.
Conclusion:
Therefore, ranking of fastest to slowest airplane is D> B> A> C.
Chapter 5 Solutions
CONCEPTUAL PHYSICS-W/PRACTICING PHYSICS
Additional Science Textbook Solutions
Campbell Biology in Focus (2nd Edition)
Microbiology with Diseases by Body System (5th Edition)
Anatomy & Physiology (6th Edition)
Microbiology: An Introduction
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
Human Physiology: An Integrated Approach (8th Edition)
- Plz no chatgpt Iarrow_forwardA = 45 kN a = 60° B = 20 kN ẞ = 30° Problem:M1.1 You and your friends are on an archaeological adventure and are trying to disarm an ancient trap to do so you need to pull a log straight out of a hole in a wall. You have 1 rope that you can attach to the log and there are currently 2 other ropes and weights attached to the end of the log. You know the force and direction of the ropes currently attached are arranged as shown below what is the magnitude and direction 'e' of the minimum force you need to apply to the third rope for the force on the log to be in direction of line 'a'? What is the resultant force in direction 'a'? a ////// //////arrow_forwardanswer both questionsarrow_forward
- - 13- 3. Shastri recalled reading that for an ideal transformer, "the ratio of the primary voltage to the secondary voltage is equal to the ratio of the secondary current to the primary current." Plan and design an experiment to investigate whether the statement above is true. (8) • With the aid of a fully labelled circuit diagram, describe a procedure which can be used to investigate whether the statement is true. The circuit diagram must include the following components: A variable AC voltage supply • AC voltmeters • AC ammeters A transformer with adjustable turns ratio Connecting wires • ° A load resistorarrow_forwardanswer question 1-6arrow_forwardFractions 1. Covert 5/7 to a decimal 2. 5/7 x 3/8 3. 2/5 divided 4/9 4. covert 37/ 19 to a decimalarrow_forward
- this is an exam past paper question that i need help with becuase i am reviewing not a graded assignmentarrow_forwardsunny (1) -13- end. One box contains nothing inside; one has a piece of resistance wire between the terminals You are provided with three sealed identical matchboxes labelled A, B and C, with terminals at each and the other, a semi-conductor diode. Plan and design an experiment to identify the contents of each box. You are provided with the following elements for your apparatus: Ammeter Low voltage power supply Connecting wires Labelled circuit diagram Draw a well-labelled circuit diagram to show how you would connect the apparatus listed above to each matchbox. (3 maarrow_forwardRAD127 Radiographic Equipment and Computers SI Units in Radiography Ch. 1 & 2 Instructions: Provide the units for each of the following in full and short forms 1. Mass - kg, 9 or (1b)) ・ 2. Energy, Work - W = FD,J 3. Air kerma -(Gya) 4. Absorbed Dose- 5. Effective Dose J/kg (94+) jlkg J/kg, Sv 6. Radioactivity - 5-1, Bq 7. Weight 8. Time 9. Force 10. Power B9 wt, wt-mg, N -(s) F= ma, N, OR 1b. (JIS), P= work It = Fdlt, Jarrow_forward
- answer 1-8arrow_forward1 . Solve the equation 2/7=y/3 for y. 2. Solve the equation x/9=2/6 for x. 3. Solve the equation z + 4 = 10 This is algebra and the equation is fraction.arrow_forwardtwo satellites are in circular orbits around the Earth. Satellite A is at an altitude equal to the Earth's radius, while satellite B is at an altitude equal to twice the Earth's radius. What is the ratio of their periods, Tb/Taarrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON





