EXCURSIONS IN MODERN MATH
5th Edition
ISBN: 9781323741559
Author: Tannenbaum
Publisher: PEARSON C
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5, Problem 14E
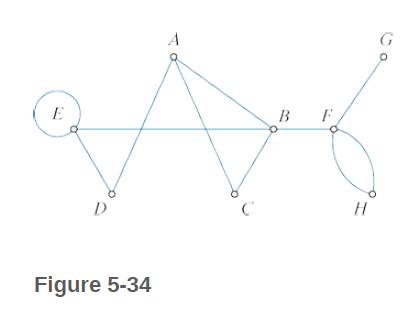
Consider the graph in Fig 5-34
a. Find all circuits of length 1. (Hint: Loops are circuits of length 1).
b. Find all circuits of length 2.
c. Find all circuits of length 3.
d. Find all circuits of length 4.
e. Find all circuits of length 5.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
No chatgpt pls will upvote
Already got wrong chatgpt answer
.
In a town with 5000 adults, a sample of 50 is selected using SRSWOR and asked their opinion of a proposed municipal project; 30 are found to favor it and 20 oppose it. If, in fact, the adults of the town were equally divided on the proposal, what would be the probability of observing what has been observed? Approximate using the Binomial distribution. Compare this with the exact probability which is 0.0418.
1.2.19. Let and s be natural numbers. Let G be the simple graph with vertex set
Vo... V„−1 such that v; ↔ v; if and only if |ji| Є (r,s). Prove that S has exactly k
components, where k is the greatest common divisor of {n, r,s}.
Chapter 5 Solutions
EXCURSIONS IN MODERN MATH
Ch. 5 - For the graph shown in Fig 5-29, a.give the vertex...Ch. 5 - For the graph shown in Fig. 5-30, a.give the...Ch. 5 - For the graph shown in Fig. 5-31, 1.give the...Ch. 5 - For the graph shown in Fig. 5-32, a.give the...Ch. 5 - Consider the graph with vertex set {K,R,S,T,W} and...Ch. 5 - Consider the graph with vertex set {A,B,C,D,E} and...Ch. 5 - Consider the graph with vertex set {A,B,C,D,E} and...Ch. 5 - Consider the graph with vertex set {A,B,C,X,Y,Z}...Ch. 5 - a.Give an example of a connected graph with eight...Ch. 5 - a.Give an example of a connected graph with eight...
Ch. 5 - Consider the graph in Fig. 5-33. a. Find a path...Ch. 5 - Consider the graph in Fig. 5-33. a. Find a path...Ch. 5 - Consider the graph in Fig. 5-33. a. Find all...Ch. 5 - Consider the graph in Fig 5-34 a.Find all circuits...Ch. 5 - List all the bridges in each of the following...Ch. 5 - List all the bridges in each of the following...Ch. 5 - Consider the graph in Fig 5-35. a. List all the...Ch. 5 - Consider the graph in Fig 5-36. a. List all the...Ch. 5 - Figure 5-37 shows a map of the downtown area of...Ch. 5 - Figure 5-38 is a map of downtown Royalton, showing...Ch. 5 - A night watchman must walk the streets of the...Ch. 5 - A mail carrier must deliver mail on foot along the...Ch. 5 - Six teams (A,B,C,D,E,andF) are entered in a...Ch. 5 - The Kangaroo Lodge of Madison Country has 10...Ch. 5 - Table 5-3 summarizes the Facebook friendships...Ch. 5 - The Dean of students office wants to know how the...Ch. 5 - Figure 5-40 shows the downtown area of the small...Ch. 5 - Prob. 28ECh. 5 - In Exercise 29 through 34 choose from the...Ch. 5 - In Exercise 29 through 34 choose from the...Ch. 5 - In Exercise 29 through 34 choose from the...Ch. 5 - In Exercises 29 through 34 choose from the...Ch. 5 - In Exercise 29 through 34 choose from the...Ch. 5 - In Exercise 29 through 34 choose from the...Ch. 5 - Find the Euler circuit for the graph in Fig.5-47....Ch. 5 - Find the Euler circuit for the graph in Fig.5.48_....Ch. 5 - Find the Euler path for the graph in Fig.5-49_....Ch. 5 - Find the Euler path for the graph in Fig.5-50....Ch. 5 - Find an Euler circuit for the graph in Fig 5-51....Ch. 5 - Find the Euler circuit for the graph in Fig 5-52....Ch. 5 - Suppose you are using Fleurys algorithm to find an...Ch. 5 - Suppose you are using Fleurys algorithm to find an...Ch. 5 - Find an optimal eulerization for the graph in Fig...Ch. 5 - Find an optimal eulerization for the graph in Fig....Ch. 5 - Find an optimal eulerization for the graph in Fig....Ch. 5 - Find an optimal eulerization for the graph in Fig...Ch. 5 - Find an optimal semi-eulerization for the graph in...Ch. 5 - Find an optimal semi-eulerization for the graph in...Ch. 5 - Prob. 49ECh. 5 - Prob. 50ECh. 5 - Prob. 51ECh. 5 - Prob. 52ECh. 5 - A security guard must patrol on foot the streets...Ch. 5 - A mail carrier must deliver mail on foot along the...Ch. 5 - This exercise refers to the Fourth of July parade...Ch. 5 - This exercise refers to the Fourth of July parade...Ch. 5 - Consider the following puzzle: You must trace Fig...Ch. 5 - a.Explain why in every graph the sum of the...Ch. 5 - Prob. 59ECh. 5 - Regular graphs. A graph is called regular if every...Ch. 5 - Suppose G is a disconnected graph with exactly two...Ch. 5 - Consider the following game. You are given N...Ch. 5 - Figure 5-59 shows a map of the downtown area of...Ch. 5 - Kissing circuits. When two circuits in a graph...Ch. 5 - Prob. 65ECh. 5 - Exercises 66 through 68 refer to Example 5.23 . In...Ch. 5 - Exercises 66 through 68 refer to Example 5.23 . In...Ch. 5 - Exercises 66 through 68 refer to Example 5.23 . In...Ch. 5 - This exercise comes to you courtesy of Euler...Ch. 5 - Running Suppose G is a connected graph with N...Ch. 5 - Running Suppose G is a connected graph with N2...Ch. 5 - Running Complete bipartite graphs. A complete...Ch. 5 - Running Suppose G is a simple graph with N...
Additional Math Textbook Solutions
Find more solutions based on key concepts
1. How much money is Joe earning when he’s 30?
Pathways To Math Literacy (looseleaf)
The largest polynomial that divides evenly into a list of polynomials is called the _______.
Elementary & Intermediate Algebra
For Problems 23-28, write in simpler form, as in Example 4. logbFG
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
1. How is a sample related to a population?
Elementary Statistics: Picturing the World (7th Edition)
(a) Make a stem-and-leaf plot for these 24 observations on the number of customers who used a down-town CitiBan...
APPLIED STAT.IN BUS.+ECONOMICS
Find E(X) for each of the distributions given in Exercise 2.1-3.
Probability And Statistical Inference (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Question 3 over a field K. In this question, MË(K) denotes the set of n × n matrices (a) Suppose that A Є Mn(K) is an invertible matrix. Is it always true that A is equivalent to A-¹? Justify your answer. (b) Let B be given by 8 B = 0 7 7 0 -7 7 Working over the field F2 with 2 elements, compute the rank of B as an element of M2(F2). (c) Let 1 C -1 1 [4] [6] and consider C as an element of M3(Q). Determine the minimal polynomial mc(x) and hence, or otherwise, show that C can not be diagonalised. [7] (d) Show that C in (c) considered as an element of M3(R) can be diagonalised. Write down all the eigenvalues. Show your working. [8]arrow_forward16. Solve the given differential equation: y" + 4y sin (t)u(t 2π), - y(0) = 1, y'(0) = 0 Given, 1 (x² + 1)(x²+4) 1/3 -1/3 = + x²+1 x² +4 Send your answer in pen and paper don't r eputed ur self down Don't send the same previous answer that was Al generated Don't use any Al tool show ur answer in pe n and paper then takearrow_forwardR denotes the field of real numbers, Q denotes the field of rationals, and Fp denotes the field of p elements given by integers modulo p. You may refer to general results from lectures. Question 1 For each non-negative integer m, let R[x]m denote the vector space consisting of the polynomials in x with coefficients in R and of degree ≤ m. x²+2, V3 = 5. Prove that (V1, V2, V3) is a linearly independent (a) Let vi = x, V2 = list in R[x] 3. (b) Let V1, V2, V3 be as defined in (a). Find a vector v € R[×]3 such that (V1, V2, V3, V4) is a basis of R[x] 3. [8] [6] (c) Prove that the map ƒ from R[x] 2 to R[x]3 given by f(p(x)) = xp(x) — xp(0) is a linear map. [6] (d) Write down the matrix for the map ƒ defined in (c) with respect to the basis (2,2x + 1, x²) of R[x] 2 and the basis (1, x, x², x³) of R[x] 3. [5]arrow_forward
- Question 4 (a) The following matrices represent linear maps on R² with respect to an orthonormal basis: = [1/√5 2/√5 [2/√5 -1/√5] " [1/√5 2/√5] A = B = [2/√5 1/√5] 1 C = D = = = [ 1/3/5 2/35] 1/√5 2/√5 -2/√5 1/√5' For each of the matrices A, B, C, D, state whether it represents a self-adjoint linear map, an orthogonal linear map, both, or neither. (b) For the quadratic form q(x, y, z) = y² + 2xy +2yz over R, write down a linear change of variables to u, v, w such that q in these terms is in canonical form for Sylvester's Law of Inertia. [6] [4]arrow_forwardpart b pleasearrow_forwardQuestion 5 (a) Let a, b, c, d, e, ƒ Є K where K is a field. Suppose that the determinant of the matrix a cl |df equals 3 and the determinant of determinant of the matrix a+3b cl d+3e f ГЪ e [ c ] equals 2. Compute the [5] (b) Calculate the adjugate Adj (A) of the 2 × 2 matrix [1 2 A = over R. (c) Working over the field F3 with 3 elements, use row and column operations to put the matrix [6] 0123] A = 3210 into canonical form for equivalence and write down the canonical form. What is the rank of A as a matrix over F3? 4arrow_forward
- Question 2 In this question, V = Q4 and - U = {(x, y, z, w) EV | x+y2w+ z = 0}, W = {(x, y, z, w) € V | x − 2y + w − z = 0}, Z = {(x, y, z, w) € V | xyzw = 0}. (a) Determine which of U, W, Z are subspaces of V. Justify your answers. (b) Show that UW is a subspace of V and determine its dimension. (c) Is VU+W? Is V = UW? Justify your answers. [10] [7] '00'arrow_forwardGood explanation it sure experts solve itarrow_forwardBest explains it not need guidelines okkarrow_forward
- Task number: A1.1, A1.7 Topic: Celestial Navigation, Compass - Magnetic and Gyro Activ Determine compass error (magnetic and gyro) using azimuth choosing a suitable celestial body (Sun/ Stars/ Planets/ Moon). Apply variation to find the deviation of the magnetic compass. Minimum number of times that activity should be recorded: 6 (2 each phase) Sample calculation (Azimuth- Planets): On 06th May 2006 at 22h20m 10s UTC, a vessel in position 48°00'N 050°00'E observed Mars bearing 327° by compass. Find the compass error. If variation was 4.0° East, calculate the deviation. GHA Mars (06d 22h): Increment (20m 10s): 089° 55.7' 005° 02.5' v (0.9): (+) 00.3' GHA Mars: 094° 58.5' Longitude (E): (+) 050° 00.0' (plus- since longitude is easterly) LHA Mars: 144° 58.5' Declination (06d 22h): d (0.2): N 024° 18.6' (-) 00.1' Declination Mars: N 024° 18.5' P=144° 58.5' (If LHA<180°, P=LHA) A Tan Latitude/ Tan P A Tan 48° 00' Tan 144° 58.5' A = 1.584646985 N (A is named opposite to latitude, except when…arrow_forwardTask number: A1.1, A1.7 Topic: Celestial Navigation, Compass - Magnetic and Gyro Activ Determine compass error (magnetic and gyro) using azimuth choosing a suitable celestial body (Sun/ Stars/ Planets/ Moon). Apply variation to find the deviation of the magnetic compass. Minimum number of times that activity should be recorded: 6 (2 each phase) Sample calculation (Azimuth- Planets): On 06th May 2006 at 22h20m 10s UTC, a vessel in position 48°00'N 050°00'E observed Mars bearing 327° by compass. Find the compass error. If variation was 4.0° East, calculate the deviation. GHA Mars (06d 22h): Increment (20m 10s): 089° 55.7' 005° 02.5' v (0.9): (+) 00.3' GHA Mars: 094° 58.5' Longitude (E): (+) 050° 00.0' (plus- since longitude is easterly) LHA Mars: 144° 58.5' Declination (06d 22h): d (0.2): N 024° 18.6' (-) 00.1' Declination Mars: N 024° 18.5' P=144° 58.5' (If LHA<180°, P=LHA) A Tan Latitude/ Tan P A Tan 48° 00' Tan 144° 58.5' A = 1.584646985 N (A is named opposite to latitude, except when…arrow_forwardActiv Determine compass error using amplitude (Sun). Minimum number of times that activity should be performed: 3 (1 each phase) Sample calculation (Amplitude- Sun): On 07th May 2006 at Sunset, a vessel in position 10°00'N 010°00'W observed the Sun bearing 288° by compass. Find the compass error. LMT Sunset: LIT: (+) 00d 07d 18h 00h 13m 40m UTC Sunset: 07d 18h 53m (added- since longitude is westerly) Declination (07d 18h): N 016° 55.5' d (0.7): (+) 00.6' Declination Sun: N 016° 56.1' Sin Amplitude = Sin Declination/Cos Latitude = Sin 016°56.1'/ Cos 10°00' = 0.295780189 Amplitude=W17.2N (The prefix of amplitude is named easterly if body is rising, and westerly if body is setting. The suffix is named same as declination) True Bearing=287.2° Compass Bearing= 288.0° Compass Error = 0.8° Westarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Minimum cuts and maximum flow rate; Author: Juddy Productions;https://www.youtube.com/watch?v=ylxhl1ipWss;License: Standard YouTube License, CC-BY