
EXCURSIONS IN MODERN MATH
5th Edition
ISBN: 9781323741559
Author: Tannenbaum
Publisher: PEARSON C
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 5, Problem 48E
Find an optimal semi-eulerization for the graph in Fig. 5-57. You are free to choose the starting and ending vertices.
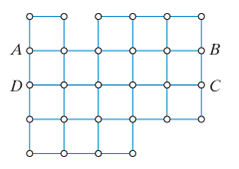
Figure 5-57
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
© ©
Q Tue 7 Jan 10:12 pm
myopenmath.com/assess2/?cid=253523&aid=17...
ookmarks
吕
Student Account...
8 Home | Participant... 001st Meeting with y...
E
F
D
c
G
B
H
I
A
J
P
K
L
N
M
Identify the special angles above. Give your answers in degrees.
A: 0
B: 30
C: 45
D: 60
E: 90
>
१
F: 120 0
G:
H:
1: 180 0
J:
K:
L: 240 0
Next-
M: 270 0
0:
ZÖÄ
N: 300 0
Aa
zoom
P:
Question Help: Message instructor
MacBook Air
Ο
O
Σ
>> | All Bookmarks
The cup on the 9th hole of a golf course is located dead center in the middle of a circular green which is 40 feet in radius. Your ball is located as in the picture below. The ball follows a straight line path and exits the green at the right-most edge. Assume the ball travels 8 ft/sec.
Introduce coordinates so that the cup is the origin of an xy-coordinate system and start by writing down the equations of the circle and the linear path of the ball. Provide numerical answers below with two decimal places of accuracy.
50 feet
green
ball
40 feet
9
cup
ball path
rough
(a) The x-coordinate of the position where the ball enters the green will be
(b) The ball will exit the green exactly
seconds after it is hit.
(c) Suppose that L is a line tangent to the boundary of the golf green and parallel to the path of the ball. Let Q be the point where the line is tangent to the circle. Notice that there are two possible positions for Q. Find the possible x-coordinates of Q:
smallest x-coordinate =…
Draw the unit circle and plot the point P=(8,2). Observe there are TWO lines tangent to the circle passing through the point P. Answer the questions below with 3 decimal places of accuracy.
P
L1
L
(a) The line L₁ is tangent to the unit circle at the point
(b) The tangent line L₁ has equation:
X +
(c) The line L₂ is tangent to the unit circle at the point (
(d) The tangent line 42 has equation:
y=
x +
).
Chapter 5 Solutions
EXCURSIONS IN MODERN MATH
Ch. 5 - For the graph shown in Fig 5-29, a.give the vertex...Ch. 5 - For the graph shown in Fig. 5-30, a.give the...Ch. 5 - For the graph shown in Fig. 5-31, 1.give the...Ch. 5 - For the graph shown in Fig. 5-32, a.give the...Ch. 5 - Consider the graph with vertex set {K,R,S,T,W} and...Ch. 5 - Consider the graph with vertex set {A,B,C,D,E} and...Ch. 5 - Consider the graph with vertex set {A,B,C,D,E} and...Ch. 5 - Consider the graph with vertex set {A,B,C,X,Y,Z}...Ch. 5 - a.Give an example of a connected graph with eight...Ch. 5 - a.Give an example of a connected graph with eight...
Ch. 5 - Consider the graph in Fig. 5-33. a. Find a path...Ch. 5 - Consider the graph in Fig. 5-33. a. Find a path...Ch. 5 - Consider the graph in Fig. 5-33. a. Find all...Ch. 5 - Consider the graph in Fig 5-34 a.Find all circuits...Ch. 5 - List all the bridges in each of the following...Ch. 5 - List all the bridges in each of the following...Ch. 5 - Consider the graph in Fig 5-35. a. List all the...Ch. 5 - Consider the graph in Fig 5-36. a. List all the...Ch. 5 - Figure 5-37 shows a map of the downtown area of...Ch. 5 - Figure 5-38 is a map of downtown Royalton, showing...Ch. 5 - A night watchman must walk the streets of the...Ch. 5 - A mail carrier must deliver mail on foot along the...Ch. 5 - Six teams (A,B,C,D,E,andF) are entered in a...Ch. 5 - The Kangaroo Lodge of Madison Country has 10...Ch. 5 - Table 5-3 summarizes the Facebook friendships...Ch. 5 - The Dean of students office wants to know how the...Ch. 5 - Figure 5-40 shows the downtown area of the small...Ch. 5 - Prob. 28ECh. 5 - In Exercise 29 through 34 choose from the...Ch. 5 - In Exercise 29 through 34 choose from the...Ch. 5 - In Exercise 29 through 34 choose from the...Ch. 5 - In Exercises 29 through 34 choose from the...Ch. 5 - In Exercise 29 through 34 choose from the...Ch. 5 - In Exercise 29 through 34 choose from the...Ch. 5 - Find the Euler circuit for the graph in Fig.5-47....Ch. 5 - Find the Euler circuit for the graph in Fig.5.48_....Ch. 5 - Find the Euler path for the graph in Fig.5-49_....Ch. 5 - Find the Euler path for the graph in Fig.5-50....Ch. 5 - Find an Euler circuit for the graph in Fig 5-51....Ch. 5 - Find the Euler circuit for the graph in Fig 5-52....Ch. 5 - Suppose you are using Fleurys algorithm to find an...Ch. 5 - Suppose you are using Fleurys algorithm to find an...Ch. 5 - Find an optimal eulerization for the graph in Fig...Ch. 5 - Find an optimal eulerization for the graph in Fig....Ch. 5 - Find an optimal eulerization for the graph in Fig....Ch. 5 - Find an optimal eulerization for the graph in Fig...Ch. 5 - Find an optimal semi-eulerization for the graph in...Ch. 5 - Find an optimal semi-eulerization for the graph in...Ch. 5 - Prob. 49ECh. 5 - Prob. 50ECh. 5 - Prob. 51ECh. 5 - Prob. 52ECh. 5 - A security guard must patrol on foot the streets...Ch. 5 - A mail carrier must deliver mail on foot along the...Ch. 5 - This exercise refers to the Fourth of July parade...Ch. 5 - This exercise refers to the Fourth of July parade...Ch. 5 - Consider the following puzzle: You must trace Fig...Ch. 5 - a.Explain why in every graph the sum of the...Ch. 5 - Prob. 59ECh. 5 - Regular graphs. A graph is called regular if every...Ch. 5 - Suppose G is a disconnected graph with exactly two...Ch. 5 - Consider the following game. You are given N...Ch. 5 - Figure 5-59 shows a map of the downtown area of...Ch. 5 - Kissing circuits. When two circuits in a graph...Ch. 5 - Prob. 65ECh. 5 - Exercises 66 through 68 refer to Example 5.23 . In...Ch. 5 - Exercises 66 through 68 refer to Example 5.23 . In...Ch. 5 - Exercises 66 through 68 refer to Example 5.23 . In...Ch. 5 - This exercise comes to you courtesy of Euler...Ch. 5 - Running Suppose G is a connected graph with N...Ch. 5 - Running Suppose G is a connected graph with N2...Ch. 5 - Running Complete bipartite graphs. A complete...Ch. 5 - Running Suppose G is a simple graph with N...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Introduce yourself and describe a time when you used data in a personal or professional decision. This could be anything from analyzing sales data on the job to making an informed purchasing decision about a home or car. Describe to Susan how to take a sample of the student population that would not represent the population well. Describe to Susan how to take a sample of the student population that would represent the population well. Finally, describe the relationship of a sample to a population and classify your two samples as random, systematic, cluster, stratified, or convenience.arrow_forwardAnswersarrow_forwardWhat is a solution to a differential equation? We said that a differential equation is an equation that describes the derivative, or derivatives, of a function that is unknown to us. By a solution to a differential equation, we mean simply a function that satisfies this description. 2. Here is a differential equation which describes an unknown position function s(t): ds dt 318 4t+1, ds (a) To check that s(t) = 2t2 + t is a solution to this differential equation, calculate you really do get 4t +1. and check that dt' (b) Is s(t) = 2t2 +++ 4 also a solution to this differential equation? (c) Is s(t)=2t2 + 3t also a solution to this differential equation? ds 1 dt (d) To find all possible solutions, start with the differential equation = 4t + 1, then move dt to the right side of the equation by multiplying, and then integrate both sides. What do you get? (e) Does this differential equation have a unique solution, or an infinite family of solutions?arrow_forward
- these are solutions to a tutorial that was done and im a little lost. can someone please explain to me how these iterations function, for example i Do not know how each set of matrices produces a number if someine could explain how its done and provide steps it would be greatly appreciated thanks.arrow_forwardQ1) Classify the following statements as a true or false statements a. Any ring with identity is a finitely generated right R module.- b. An ideal 22 is small ideal in Z c. A nontrivial direct summand of a module cannot be large or small submodule d. The sum of a finite family of small submodules of a module M is small in M A module M 0 is called directly indecomposable if and only if 0 and M are the only direct summands of M f. A monomorphism a: M-N is said to split if and only if Ker(a) is a direct- summand in M & Z₂ contains no minimal submodules h. Qz is a finitely generated module i. Every divisible Z-module is injective j. Every free module is a projective module Q4) Give an example and explain your claim in each case a) A module M which has two composition senes 7 b) A free subset of a modale c) A free module 24 d) A module contains a direct summand submodule 7, e) A short exact sequence of modules 74.arrow_forward************* ********************************* Q.1) Classify the following statements as a true or false statements: a. If M is a module, then every proper submodule of M is contained in a maximal submodule of M. b. The sum of a finite family of small submodules of a module M is small in M. c. Zz is directly indecomposable. d. An epimorphism a: M→ N is called solit iff Ker(a) is a direct summand in M. e. The Z-module has two composition series. Z 6Z f. Zz does not have a composition series. g. Any finitely generated module is a free module. h. If O→A MW→ 0 is short exact sequence then f is epimorphism. i. If f is a homomorphism then f-1 is also a homomorphism. Maximal C≤A if and only if is simple. Sup Q.4) Give an example and explain your claim in each case: Monomorphism not split. b) A finite free module. c) Semisimple module. d) A small submodule A of a module N and a homomorphism op: MN, but (A) is not small in M.arrow_forward
- Prove that Σ prime p≤x p=3 (mod 10) 1 Ρ = for some constant A. log log x + A+O 1 log x "arrow_forwardProve that, for x ≥ 2, d(n) n2 log x = B ― +0 X (금) n≤x where B is a constant that you should determine.arrow_forwardProve that, for x ≥ 2, > narrow_forwardI need diagram with solutionsarrow_forwardT. Determine the least common denominator and the domain for the 2x-3 10 problem: + x²+6x+8 x²+x-12 3 2x 2. Add: + Simplify and 5x+10 x²-2x-8 state the domain. 7 3. Add/Subtract: x+2 1 + x+6 2x+2 4 Simplify and state the domain. x+1 4 4. Subtract: - Simplify 3x-3 x²-3x+2 and state the domain. 1 15 3x-5 5. Add/Subtract: + 2 2x-14 x²-7x Simplify and state the domain.arrow_forwardQ.1) Classify the following statements as a true or false statements: Q a. A simple ring R is simple as a right R-module. b. Every ideal of ZZ is small ideal. very den to is lovaginz c. A nontrivial direct summand of a module cannot be large or small submodule. d. The sum of a finite family of small submodules of a module M is small in M. e. The direct product of a finite family of projective modules is projective f. The sum of a finite family of large submodules of a module M is large in M. g. Zz contains no minimal submodules. h. Qz has no minimal and no maximal submodules. i. Every divisible Z-module is injective. j. Every projective module is a free module. a homomorp cements Q.4) Give an example and explain your claim in each case: a) A module M which has a largest proper submodule, is directly indecomposable. b) A free subset of a module. c) A finite free module. d) A module contains no a direct summand. e) A short split exact sequence of modules.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
 Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning


Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning

College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY