The Heart of Mathematics: An Invitation to Effective Thinking
4th Edition
ISBN: 9781118156599
Author: Edward B. Burger, Michael Starbird
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 4.6, Problem 38MS
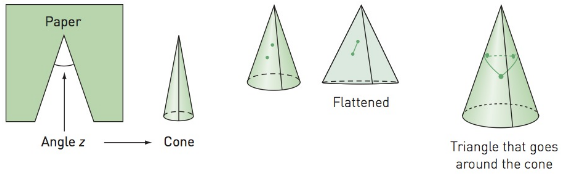
Removing a slice of the pie. Complete the following table by making the cones, drawing triangles around the cone points, measuring the angles of the triangles, and adding them up.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Can you evalutate the following summation:∑_{y=1}^{x} 2 / ((x + y - 1)(x + y + 1))
A retail chain is interested in determining whether a digital video point-of-purchase (POP) display would stimulate higher sales for a brand advertised compared to the standard cardboard point-of-purchase display. To test this, a one-shot static group design experiment was conducted over a four-week period in 100 different stores. Fifty stores were randomly assigned to the control treatment (standard display) and the other 50 stores were randomly assigned to the experimental treatment (digital display). Compare the sales of the control group (standard POP) to the experimental group (digital POP).
What were the average sales for the standard POP display (control group)?
What were the sales for the digital display (experimental group)?
What is the (mean) difference in sales between the experimental group and control group?
List the null hypothesis being tested.
Do you reject or retain the null hypothesis based on the results of the independent t-test?
Was the difference between the…
Can you evaluate the following summation:∑_{k=1}^{n} (4log(n+k) + 4k)
Chapter 4 Solutions
The Heart of Mathematics: An Invitation to Effective Thinking
Ch. 4.1 - The main event. State the Pythagorean Theorem.Ch. 4.1 - Two out of three. If a right triangle has legs of...Ch. 4.1 - Hypotenuse hype. If a right triangle has legs of...Ch. 4.1 - Assesing area. Suppose you know the base of a...Ch. 4.1 - Squares all around. How does the figure below...Ch. 4.1 - Operating on the triangle. Using a straightedge,...Ch. 4.1 - Excite your friends about right triangles....Ch. 4.1 - Easy as 1,2,3? Can there be a right triangle with...Ch. 4.1 - Sky high (S). On a sunny, warm day, a student...Ch. 4.1 - Sand masting (H). The sailboat named Sand Bug has...
Ch. 4.1 - Getting a pole on a bus. For his 13th birthday,...Ch. 4.1 - The Scarecrow (ExH). In the 1939 movie The Wizard...Ch. 4.1 - Rooting through a spiral. Start with a right...Ch. 4.1 - Is it right? (H) Suppose someone tells you that...Ch. 4.1 - Tfrain trouble (H). Train tracks are made of...Ch. 4.1 - Does everyone have what it takes to be a triangle?...Ch. 4.1 - Getting squared away. In our proof of the...Ch. 4.1 - The practical side of Pythagoras. Suppose you are...Ch. 4.1 - Pythagorean pizzas (H). You have a choice at the...Ch. 4.1 - Natural right (S). Suppose r and s are any two...Ch. 4.1 - Well-rounded shapes. Suppose we have two circles...Ch. 4.1 - A Pythagorean Theorem for triangles other than...Ch. 4.1 - With a group of folks. In a small group, discuss...Ch. 4.1 - Double trouble. Suppose you know a right triangle...Ch. 4.1 - K-ple trouble. Suppose you have a right triangle...Ch. 4.1 - Padding around. You have a rectangular patio with...Ch. 4.1 - Pythagoras goes the distance. Plot the points (5,...Ch. 4.1 - Ahoy there! (H) Your exotic sailboat, which you...Ch. 4.2 - Standing guard. Draw the floor plan of a gallery...Ch. 4.2 - Art appreciation. State the Art Gallery Theorem.Ch. 4.2 - Upping the ante. How many guards do you need for a...Ch. 4.2 - Keep it safe. At what vertices would you place...Ch. 4.2 - Puttoing guards in their place. For each floor...Ch. 4.2 - Guarding the Guggenheim. The Art Gallery Theorem...Ch. 4.2 - TriangulatIng the Louvre (H). Triangulate the...Ch. 4.2 - Triangulating the Clark. Triangulate the floor...Ch. 4.2 - Tricolor me (ExH). For each triangulation, color...Ch. 4.2 - Tricolor hue. For each triangulation, color the...Ch. 4.2 - One-third. Write the number 6 as a sum of three...Ch. 4.2 - Easy watch. Draw a floor plan of a museum with six...Ch. 4.2 - Two watches (S). Draw the floor plan of a museum...Ch. 4.2 - Mirror, mirror on the wall. Consider the floor...Ch. 4.2 - Nine needs three (H). Draw a floor plan for a...Ch. 4.2 - One-third again (ExH). If a natural number is...Ch. 4.2 - Square museum (S). If a museum has only...Ch. 4.2 - Worst squares (H). Draw examples of museums with...Ch. 4.2 - Pie are squared. The circumference of a circle of...Ch. 4.2 - I can see the light. Suppose you are in a...Ch. 4.2 - Less than. Youve tnangulated your polygon and...Ch. 4.2 - Greater than. Youve triangulated your polygon and...Ch. 4.2 - Counting the colors. Your polygon has 40 vertices....Ch. 4.2 - Only red. Twelve of your polygons vertices have...Ch. 4.2 - Totaling triangles. If a polygon has n sides, it...Ch. 4.3 - Defining gold. Explain what makes a rectangle a...Ch. 4.3 - Approximating gold. Which of these numbers is...Ch. 4.3 - Approximating again. Which of the following...Ch. 4.3 - Same solution. Why does the equation l1=1l have...Ch. 4.3 - X marks the unkonw (ExH). Solve eachh equation for...Ch. 4.3 - A cold tall one? Can a Golden Rectangle have a...Ch. 4.3 - Fold the gold (H). Suppose you have a Golden...Ch. 4.3 - Sheets of gold. Suppose you have two sheets of...Ch. 4.3 - Circular logic? (H). Take a Golden Rectangle and...Ch. 4.3 - Growing gold (H). Take a Golden Rectangle and...Ch. 4.3 - Counterfeit gold? Draw a rectangle with its longer...Ch. 4.3 - In the grid (S). Consider the 1010 grid at left....Ch. 4.3 - A nest of gold. Consider the figure of infinitely...Ch. 4.3 - Comparing areas (ExH). Let G be a Golden Rectangle...Ch. 4.3 - Do we get gold? Lets make a rectangle somewhat...Ch. 4.3 - Do we get gold this time? (S) We now describe...Ch. 4.3 - A silver lining? (H) Consider the diagonal in the...Ch. 4.3 - Prob. 20MSCh. 4.3 - Going platinum. Determine the dimensions of a...Ch. 4.3 - Golden triangles. Draw a right triangle with one...Ch. 4.3 - Prob. 23MSCh. 4.3 - Prob. 24MSCh. 4.3 - Prob. 25MSCh. 4.3 - Power beyond the mathematics. Provide several...Ch. 4.3 - Special K. As a student at the University of...Ch. 4.3 - Special x. Find all values of x satisfying the...Ch. 4.3 - In search of x. Solve each equation for x:...Ch. 4.3 - Adding a square. Your school Healthy Eating garden...Ch. 4.3 - Golden Pythagoras (H). If you have a Golden...Ch. 4.4 - To tile or not to tile. Which of the following...Ch. 4.4 - Shifting Into symmetry. Shown below are small...Ch. 4.4 - Prob. 3MSCh. 4.4 - Prob. 4MSCh. 4.4 - Symmetric scaling (ExH). Each of the two patterns...Ch. 4.4 - Build a super. Draw a 1,2,5 right triangle in the...Ch. 4.4 - Another angle. Look at the 5-unit super-tile you...Ch. 4.4 - Super-super. Surround your 5-unit super-tile with...Ch. 4.4 - Expand forever (H). If you continue the process of...Ch. 4.4 - Prob. 10MSCh. 4.4 - Expand again. Take your 4.unit equilateral...Ch. 4.4 - One-answer supers. Here is a Pinwheel Pattern. For...Ch. 4.4 - Prob. 14MSCh. 4.4 - Many answer supers (H). Shown here are pictures of...Ch. 4.4 - Fill er up? (ExH) For each tile below, could...Ch. 4.4 - Prob. 18MSCh. 4.4 - Prob. 19MSCh. 4.4 - Prob. 20MSCh. 4.4 - Penrose tiles. Roger Penrose constructed two tiles...Ch. 4.4 - Expand forever. Why does any shape that can be...Ch. 4.4 - Super total. Recall that the Pinwheel Triangle has...Ch. 4.4 - Prob. 26MSCh. 4.4 - XY-tiles. The trapezoidal tile on the left has one...Ch. 4.4 - School spirit. Your dorm bathroom is tiled using...Ch. 4.4 - T-total (H). Suppose you start with one small...Ch. 4.5 - Its nice to be regular. What makes a polygon a...Ch. 4.5 - Keeping it Platonic. What makes a solid a regular...Ch. 4.5 - Countem up. How many faces, edges, and vertices...Ch. 4.5 - Defending duality. Explain why the cube and the...Ch. 4.5 - The eye of the beholder. Suppose you have models...Ch. 4.5 - Drawing solids. Draw each solid by completing the...Ch. 4.5 - Count. For each of the regular solids, take the...Ch. 4.5 - Soccer counts (ExH). Look at a soccer ball. Take...Ch. 4.5 - A solid slice (S). For each regular solid, imagine...Ch. 4.5 - Siding on the cube. Suppose we start with the...Ch. 4.5 - Cube slices (H). Consider slicing the cube with a...Ch. 4.5 - Dual quads (S). Suppose you have a cube with edges...Ch. 4.5 - Super dual. Suppose you take a cube with edges of...Ch. 4.5 - Self-duals. Suppose you have a tetrahedron having...Ch. 4.5 - Not quite regular (ExH). Suppose you allow...Ch. 4.5 - Truncated solids. Slice off all the vertices of...Ch. 4.5 - Stellated solids. Take each regular solid and...Ch. 4.5 - Prob. 24MSCh. 4.5 - Here we celeb rate the power of algebra as a...Ch. 4.5 - Here we celeb rate the power of algebra as a...Ch. 4.5 - Here we celeb rate the power of algebra as a...Ch. 4.5 - Here we celeb rate the power of algebra as a...Ch. 4.5 - Here we celeb rate the power of algebra as a...Ch. 4.6 - Walkind the walk. Here are three walks from corner...Ch. 4.6 - Missing angle in action. The triangles below are...Ch. 4.6 - Slippery X. A triangle is drawn on a sphere. Can...Ch. 4.6 - A triangular trio. The sphere below has three...Ch. 4.6 - Saddle sores. The triangle at right is drawn on a...Ch. 4.6 - Travel agent. In each of the following three...Ch. 4.6 - Travel agent. In each of the following three...Ch. 4.6 - Travel agent. In each of the following three...Ch. 4.6 - Latitude losers (H). In each of the following...Ch. 4.6 - Latitude losers (H). In each of the following...Ch. 4.6 - Latitude losers (H). In each of the following...Ch. 4.6 - Spider and bug. For each pair of points on the...Ch. 4.6 - Spider and bug. For each pair of points on the...Ch. 4.6 - Spider and bug. For each pair of points on the...Ch. 4.6 - Spider and bug. For each pair of points on the...Ch. 4.6 - Spider and bug. For each pair of points on the...Ch. 4.6 - Big angles (H). What is the largest value we can...Ch. 4.6 - Many angles (S). Draw three different great...Ch. 4.6 - Quads in a plane. Measure the sum of the angles of...Ch. 4.6 - Quads on the sphere. Below are quadrilaterals on...Ch. 4.6 - Parallel lines (ExH). On a plane, if you draw a...Ch. 4.6 - Cubical spheres (ExH). Take a cube. Put a point in...Ch. 4.6 - Tetrahedral spheres. Lets do a similar calculation...Ch. 4.6 - Dodecahedral spheres. This Mindscape is the same...Ch. 4.6 - Total excess. Using the observations from the...Ch. 4.6 - What is the sum of the three angles? Why? Consider...Ch. 4.6 - What is the sum of the angles of your triangle? Is...Ch. 4.6 - Removing a slice of the pie. Complete the...Ch. 4.6 - Conjuring up a conjecture. Make a conjecture about...Ch. 4.6 - Tetrahedral angles. What is the sum of the angles...Ch. 4.6 - Here we celebrate the power of algebra as a...Ch. 4.6 - Here we celebrate the power of algebra as a...Ch. 4.6 - Here we celebrate the power of algebra as a...Ch. 4.6 - Here we celebrate the power of algebra as a...Ch. 4.6 - Here we celebrate the power of algebra as a...Ch. 4.7 - At one with the univers. Below is a sketch of a...Ch. 4.7 - Are we there yet? Why does the information x=4 not...Ch. 4.7 - Plain places. Plot the following points in the...Ch. 4.7 - Big stack. If you take a huge number of sheets of...Ch. 4.7 - A bigger stack. If you take a huge number of...Ch. 4.7 - On the level in two dimensions. Pictured in the...Ch. 4.7 - On the level in two dimensions (S). Pictured in...Ch. 4.7 - On the level in four dimensions. Pictured in the...Ch. 4.7 - Tearible 2s. In the pictures below, describe how...Ch. 4.7 - Dare not to tear? For the figures in the Tearible...Ch. 4.7 - Unlinking (H). Using the fourth dimension,...Ch. 4.7 - Unknotting. Describe how you would unknot the...Ch. 4.7 - Prob. 13MSCh. 4.7 - Edgy hypercubes (H). Produce drawings of the...Ch. 4.7 - Prob. 15MSCh. 4.7 - Prob. 16MSCh. 4.7 - Doughnuts in dimensions. Suppose we have a...Ch. 4.7 - Assembly required (S). As promised in the...Ch. 4.7 - Slicing the cube. Take a 3-dimensional cube...Ch. 4.7 - Here we celebrate the power of algebra as a...Ch. 4.7 - Here we celebrate the power of algebra as a...Ch. 4.7 - Here we celebrate the power of algebra as a...Ch. 4.7 - Here we celebrate the power of algebra as a...Ch. 4.7 - Here we celebrate the power of algebra as a...
Additional Math Textbook Solutions
Find more solutions based on key concepts
CHECK POINT 1 In a survey on musical tastes, respondents were asked: Do you listed to classical music? Do you l...
Thinking Mathematically (6th Edition)
NOTE: Write your answers using interval notation when appropriate.
CHECKING ANALYTIC SKILLS Fill in each blank ...
Graphical Approach To College Algebra
In Exercises 9–16, express the integrand as a sum of partial fractions and evaluate the integrals.
9.
University Calculus: Early Transcendentals (4th Edition)
Mathematical Connections Explain why a number and a numeral are considered different.
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Suppose that A and B are mutually exclusive events for which P(A) = .3 and P(B) = .5. What is the probability t...
A First Course in Probability (10th Edition)
Explore! Exercises 9 and 10 provide two data sets front “Graphs in Statistical Analysis,” by F J. Anscombe, the...
Elementary Statistics (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Question 4 An article in Quality Progress (May 2011, pp. 42-48) describes the use of factorial experiments to improve a silver powder production process. This product is used in conductive pastes to manufacture a wide variety of products ranging from silicon wafers to elastic membrane switches. Powder density (g/cm²) and surface area (cm/g) are the two critical characteristics of this product. The experiments involved three factors: reaction temperature, ammonium percentage, stirring rate. Each of these factors had two levels, and the design was replicated twice. The design is shown in Table 3. A222222222222233 Stir Rate (RPM) Ammonium (%) Table 3: Silver Powder Experiment from Exercise 13.23 Temperature (°C) Density Surface Area 100 8 14.68 0.40 100 8 15.18 0.43 30 100 8 15.12 0.42 30 100 17.48 0.41 150 7.54 0.69 150 8 6.66 0.67 30 150 8 12.46 0.52 30 150 8 12.62 0.36 100 40 10.95 0.58 100 40 17.68 0.43 30 100 40 12.65 0.57 30 100 40 15.96 0.54 150 40 8.03 0.68 150 40 8.84 0.75 30 150…arrow_forwardGiven sets X and Y and Z, can you prove that (X-(Y u Z)) u (Y-(X u Z)) is a subset of (X u Y) - (X intersection Y)arrow_forward4. A car travels in a straight line for one hour. Its velocity, v, in miles per hour at six minute intervals is shown in the table. For each problem, approximate the distance the car traveled (in miles) using the given method, on the provided interval, and with the given number of rectangles or trapezoids, n. Time (min) 0 6 12 18|24|30|36|42|48|54|60 Speed (mph) 0 10 20 40 60 50 40 30 40 40 65 a.) Left Rectangles, [0, 30] n=5 b.) Right Rectangles, [24, 42] n=3 c.) Midpoint Rectangles, [24, 60] n=3 d.) Trapezoids, [0, 24] n=4arrow_forward
- Given the functions A and B, can you prove that if B ◦ A is bijective, then A is injective and B is surjectivearrow_forward- + ++ Table 2: Crack Experiment for Exercise 2 A B C D Treatment Combination (1) Replicate I II 7.037 6.376 14.707 15.219 |++++ 1 བྱ॰༤༠སྦྱོ སྦྱོཋཏྟཱུ a b ab 11.635 12.089 17.273 17.815 с ас 10.403 10.151 4.368 4.098 bc abc 9.360 9.253 13.440 12.923 d 8.561 8.951 ad 16.867 17.052 bd 13.876 13.658 abd 19.824 19.639 cd 11.846 12.337 acd 6.125 5.904 bcd 11.190 10.935 abcd 15.653 15.053 Question 3 Continuation of Exercise 2. One of the variables in the experiment described in Exercise 2, heat treatment method (C), is a categorical variable. Assume that the remaining factors are continuous. (a) Write two regression models for predicting crack length, one for each level of the heat treatment method variable. What differences, if any, do you notice in these two equations? (b) Generate appropriate response surface contour plots for the two regression models in part (a). (c) What set of conditions would you recommend for the factors A, B, and D if you use heat treatment method C = +? (d) Repeat…arrow_forwardTerry has a square plot of land measuring 500 meters by 500 meters. She divided the land into 25 100-m by 100-m plots and created three raster maps showing the type of mineral, fruit tree, and energy available on each plot. Use the maps below to shade the blank maps according to each problem.arrow_forward
- The bracket BCD is hinged at C and attached to a control cable at B. Let F₁ = 275 N and F2 = 275 N. F1 B a=0.18 m C A 0.4 m -0.4 m- 0.24 m Determine the reaction at C. The reaction at C N Z F2 Darrow_forwardQuestion 2 A nickel-titanium alloy is used to make components for jet turbine aircraft engines. Cracking is a potentially serious problem in the final part because it can lead to nonrecoverable failure. A test is run at the parts producer to determine the effect of four factors on cracks. The four factors are: pouring temperature (A), titanium content (B), heat treatment method (C), amount of grain refiner used (D). Two replicates of a 24 design are run, and the length of crack (in mm x10-2) induced in a sample coupon subjected to a standard test is measured. The data are shown in Table 2. 1 (a) Estimate the factor effects. Which factor effects appear to be large? (b) Conduct an analysis of variance. Do any of the factors affect cracking? Use a = 0.05. (c) Write down a regression model that can be used to predict crack length as a function of the significant main effects and interactions you have identified in part (b). (d) Analyze the residuals from this experiment. (e) Is there an…arrow_forwardShow the stepsarrow_forward
- The correct answer is C,i know that we need to use stokes theorem and parametrize the equations then write the equation F with respect to the curve but i cant seem to find a way to do it, the integral should be from 0 to 2pi but i might be wrongcould you show me the steps to get to 18piarrow_forwardA 10-ft boom is acted upon by the 810-lb force as shown in the figure. D 6 ft 6 ft E B 7 ft C 6 ft 4 ft W Determine the tension in each cable and the reaction at the ball-and-socket joint at A. The tension in cable BD is lb. The tension in cable BE is lb. The reaction at A is ( lb) i + Ib) j. (Include a minus sign if necessary.)arrow_forwardthe correct answer is A could you show me whyarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Quadrilaterals: Missing Angles and Sides; Author: rhornfeck;https://www.youtube.com/watch?v=knVj1O0L2TM;License: Standard YouTube License, CC-BY
STD IX | State Board | Types of Quadrilateral; Author: Robomate;https://www.youtube.com/watch?v=wh0KQ4UB0EU;License: Standard YouTube License, CC-BY