
Concept explainers
To determine whether the model is a good fit for the data in the table −

Answer to Problem 7E
The model isa good fit for the data in the table.
Explanation of Solution
Given:

Formula Used:
A residual is a measure of how well a line fits an individual data point. This vertical distance is known as a residual. For data points above the line, the residual is positive, and for data points below the line, the residual is negative. The closer a data point's residual is to
Calculation:
| Residual | |||
Plotting the above points on the graph, we have:
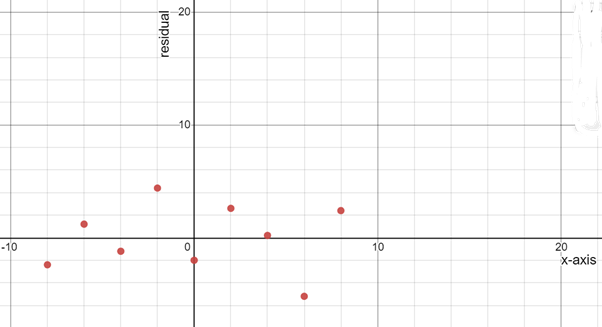
From the above graph, we can see that the residuals form a straight line.
Thus, the model isa good fit for the data in the table.
Conclusion:
The model is a good fit for the data in the table.
Chapter 4 Solutions
BIG IDEAS MATH Integrated Math 1: Student Edition 2016
- Nasir invested $415 into a savings account that earns 2.5% annual interest. Tiana invested $295 into a saving account that earns 6.8% annual interest. Who will have more money after 7 years? How much more money will the person have?arrow_forwardSolve for the variable. 62k = 7776k- 8arrow_forward2. If log2 (sin x) + log₂ (cos x) = -2 and log2 (sin x + cos x) = (-2 + log2 n), find n.arrow_forward
- If cscx- cotx = -4, find cscx + cotx.arrow_forwardQ 2/classify the zeros and poles of the function f(z) = tanz Zarrow_forward30.1. Show that z = 0 is a removable singularity of the following functions. Furthermore, define f(0) such that these functions are analytic at z = 0. (a). f(z) = 2 sin z- z 1-12² - cos z (b). f(z) = (c). f(z) = sin 22arrow_forward
- 3. Consider the polynomial equation 6-iz+7z² -iz³ +z = 0 for which the roots are 3i, -2i, -i, and i. (a) Verify the relations between this roots and the coefficients of the polynomial. (b) Find the annulus region in which the roots lie.arrow_forward30.3. Find and classify the isolated singularities of the following func- tions: (a). 23+1 22(2-1) (b). ²e¹/, (c). sin 3z (d). COS 2arrow_forward3. Consider the polynomial equation 6-iz+7z2-iz³ +z = 0 for which the roots are 3i, -2i, -i, and i. (a) Verify the relations between this roots and the coefficients of the polynomial. (b) Find the annulus region in which the roots lie.arrow_forward
- Determine the set of odd primes p for which 23 is a quadratic residue.arrow_forwardPatterns in Floor Tiling A square floor is to be tiled with square tiles as shown. There are blue tiles on the main diagonals and red tiles everywhere else. In all cases, both blue and red tiles must be used. and the two diagonals must have a common blue tile at the center of the floor. If 81 blue tiles will be used, how many red tiles will be needed? For what numbers in place of 81 would this problem still be solvable? Find an expression in k giving the number of red tiles required in general.arrow_forwardSolve questionsarrow_forward
 Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
 Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning, Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education





